本文是马同学推出的免费课《高等数学预备课》的内容，文中的习题答案、动图等，请访问微信公众号：马同学图解数学或直接访问：www.matongxue.com查阅。

就像数有了加减乘除才能解决更多的问题，集合也需要类似的基本运算来提升处理问题的能力，本课就来介绍相关的内容。

1 全集

1.1 全集

进行科学研究总需要划定适用范围，比如牛顿的经典力学的适用范围是低速运动，而爱因斯坦的相对论可以适用在高速的情况：

集合中有一个概念就是用来划定范围的：

在同一个全集中的子集，或者说在同一个范围内的集合，才有进行相互比较（指子集，真子集）、基本运算等的必要。比如代表某校学生的集合A ，和代表所有茶叶品种的集合B ，两者几乎不会相提并论，更没有进行比较、运算的并要。

所以后面的讨论都会在某个全集内进行。

1.2 全集的 Venn 图

比如某全集：

U=\{x\ |\ x\ 为所有的水果品种\}\\

在全集内有两个子集：

A=\{x\ |\ x\ 为所有的苹果品种\},\quad B=\{x\ |\ x\ 为所有的橘子品种\}\\

作这三者的 Venn 图时，常用一个方框来表示全集U ，两个子集会分别画在方框内：

2 交运算

集合的基本运算总共有 4 种，分别是交、并、差、补。下面逐一进行讲解。

让我们开始第一个运算的讲解。对于集合A、B，交运算（Intersection）被定义为：

A\cap B:=\{x|x\in A\ 且 \ x\in B\}\\

用 Venn 图可以表示如下，其中阴影为运算的结果：

反复运用上述定义，可以将交运算推广到有限个甚至无限个集合中去（其中\infty 符号代表正无穷）：

\bigcap_{n=1}^{n}S_n=S_1\cap S_2\cap\cdots\cap S_n,\quad \bigcap_{n=1}^{\infty}S_n=S_1\cap S_2\cdots\\

3 并运算

对于集合A、B，并运算（Union）被定义为：

A\cup B:=\{x|x\in A\ 或 \ x\in B\}\\

用 Venn 图可以表示如下，其中阴影为运算的结果：

反复运用上述定义，可以将并运算推广到有限个甚至无限个集合中去（其中\infty 符号代表正无穷）：

\bigcup_{n=1}^{n}S_n=S_1\cup S_2\cup\cdots\cup S_n,\quad \bigcup_{n=1}^{\infty}S_n=S_1\cup S_2\cdots\\

4 差运算

对于集合A、B，差运算（Relative Complement）被定义为：

A-B:=\{x|x\in A\quad 且\quad x\notin B\}\\

用 Venn 图可以表示如下，其中阴影为运算的结果：

5 补运算

5.1 补运算

假如有全集U 以及其子集A 、B ，满足：

A=U-B\\

则称B 为A 的补（Complement），记作：

B=\overline{A}\quad 或\quad B=\complement_UA\\

本课程中更多用\overline{A} 来表示补集，而在《高中数学人教版》中用的是\complement_UA ，拉长的 C 以及 U 表示这是在全集U 上的补集。

用 Venn 图可以表示如下，其中阴影为运算的结果：

5.2 互补

上面描述的补，反过来也是成立的：

B=\overline{A}\implies A=\overline{B}\quad 或\quad A=\complement uB\\

所以A 、B 也可以称为互补。

6 基本运算的性质

数的基本运算“乘加减”有自己的性质，集合的基本运算“交并差”也一样，并且两者的性质还差不多，下面来看看。

6.1 类比

首先，让我们将“交并差”与“乘加减”进行类比：

\begin{array}{c|c|c} \hline \quad\quad&\quad 类比\quad&\quad 改写 \quad\\ \hline \\ \quad 交 \quad&\quad \times\quad&\quad A\cap B=AB \quad\\ \quad 并 \quad&\quad +\quad&\quad A\cup B=A+B \quad\\ \quad 差 \quad&\quad -\quad&\quad A-B \quad\\ \\ \hline \end{array}\\

其实很多书籍也会把“交并差”写作“乘加减”的形式，本课程也会在不误解的情况下，交叉使用这两种符号

6.2 基本运算的性质

按照上面这样类比的话，你会发现两种基本运算的性质差不多：

\begin{array}{c|c} \hline \\ \quad 交换律 \quad&\qquad\begin{aligned}A+B=B+A\\AB=BA\quad\end{aligned} \qquad\\ \\ \hline \\ \quad 结合律 \quad&\qquad\begin{aligned}A+B+C=A+(B+C)\\ABC=A(BC)\qquad\end{aligned} \qquad\\ \\ \hline \\ \quad 分配律 \quad&\qquad\begin{aligned}(A+B)C=AC+BC\qquad\\(A-B)C=AC-BC\qquad\\(A\cap B)\cup C=(A\cup C)\cap(B\cup C)\end{aligned} \qquad\\ \\ \hline \end{array} \\

上表中用“乘加减”表示的性质既对数成立，也对集合成立。只有最后一条性质是集合独有的，所以单独用集合的运算符号来表示。

7 德摩根定律

7.1 德摩根定律

集合运算中有个德摩根定律（De Morgan's laws）需要介绍下，即：

\overline{A\cup B}=\overline{A}\cap\overline{B}\\\overline{A\cap B}=\overline{A}\cup\overline{B}\\下面来证明\overline{A\cup B}=\overline{A}\cap\overline{B} ，假设：

P=\overline{A\cup B},\quad Q=\overline{A}\cap\overline{B}\\可知，对于任意x\in P 有： \begin{aligned} x\in P &\implies x\in \overline{A\cup B}\\ &\implies x\notin (A\cup B)\\ &\implies x\notin A\ \ 且\ \ x\notin B\\ &\implies x\in\overline{A}\ \ 且\ \ x\in\overline{B}\\ &\implies x\in(\overline{A}\cap \overline{B})\\ &\implies x\in Q\\ &\implies P\subseteq Q\quad (1) \end{aligned} \\同理，对于任意y\in Q 有： \begin{aligned} y\in Q &\implies y\in(\overline{A}\cap \overline{B})\\ &\implies y\in\overline{A}\ \ 且\ \ y\in\overline{B}\\ &\implies y\notin A\ \ 且\ \ y\notin B\\ &\implies y\notin (A\cup B)\\ &\implies y\in \overline{A\cup B}\\ &\implies y\in P\\ &\implies Q\subseteq P\quad (2) \end{aligned} \\结合（1）（2）可得：P=Q\implies \overline{A\cup B}=\overline{A}\cap\overline{B}\\\overline{A\cap B}=\overline{A}\cup\overline{B} 同理可证。 \blacksquare

德摩根定律用生活中的例子也很好理解，假设A 代表“去跑步”，B 代表“去跳远”，A\cup B 表示“去跑步或跳远”，所以有：

\underbrace{\overline{A\cup B}}_{\large “不去跑步或跳远”}=\underbrace{\overline{A}\cap\overline{B}}_{\large “既不去跑步也不去跳远”}\\

而A\cap B 表示“既跑步又跳远”，所以有：

\underbrace{\overline{A\cap B}}_{\large “不既跑步又跳远”}=\underbrace{\overline{A}\cup\overline{B}}_{\large “不去跑步或者不去跳远”}\\

7.2 Venn 图

也可以通过 Venn 图来理解德摩根定律，首先是第一个公式\overline{A\cup B}=\overline{A}\cap\overline{B} ：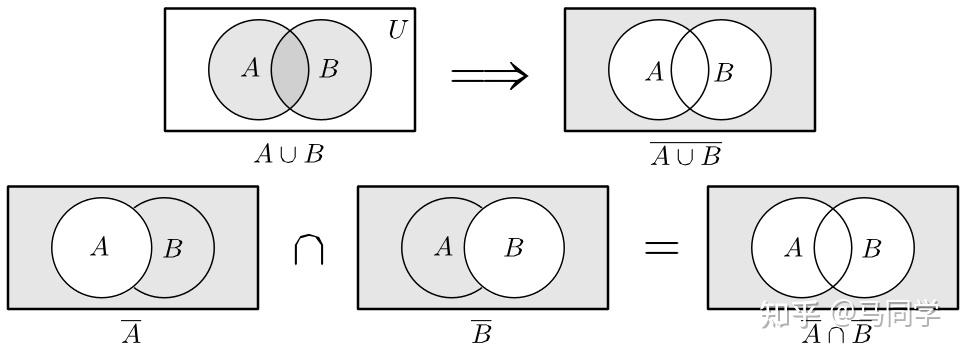

然后是第二个公式\overline{A\cap B}=\overline{A}\cup\overline{B} ：

7.3 记忆方法

理解归理解，德摩根定律看上去还是有点复杂，可以通过下面方法来记忆，就是头顶上的帽子断开时，中间的符号要翻转：

德摩根定律拓展到多个事件上也是成立的，记忆方法也是一样的：

\overline{A_1\cup A_2\cup\cdots\cup A_n}=\overline{A_1}\cap\overline{A_2}\cap\cdots\cap\overline{A_n}\\

\overline{A_1\cap A_2\cap\cdots\cap A_n}=\overline{A_1}\cup\overline{A_2}\cup\cdots\cup\overline{A_n}\\

8 互动操作

下面是一个互动操作，可以通过点击单选按钮来看到不同的 Venn 图，这样或许可以帮助同学们加深对集合各种运算的理解：

9 py：集合的基本运算

通过 numpy 也可以完成集合的基本运算：

运行结果

至于集合基本运算的性质和德摩根定律，同学们可以尝试去实现下。

10 小结

这节课我们介绍了集合的基本运算：

以及基本运行的性质和德摩根定律：

\begin{array}{c|c} \hline \\ \quad 交换律 \quad&\qquad\begin{aligned}A+B=B+A\\AB=BA\quad\end{aligned} \qquad\\ \\ \hline \\ \quad 结合律 \quad&\qquad\begin{aligned}A+B+C=A+(B+C)\\ABC=A(BC)\qquad\end{aligned} \qquad\\ \\ \hline \\ \quad 分配律 \quad&\qquad\begin{aligned}(A+B)C=AC+BC\qquad\\(A-B)C=AC-BC\qquad\\(A\cap B)\cup C=(A\cup C)\cap(B\cup C)\end{aligned} \qquad\\ \\ \hline \\ \quad 德摩根定律 \quad&\qquad\begin{aligned}\overline{A\cup B}=\overline{A}\cap\overline{B}\\\overline{A\cap B}=\overline{A}\cup\overline{B}\end{aligned} \qquad\\ \\ \hline \end{array} \\ 更多内容推荐马同学图解数学系列教程