离散数学知识点总结(10)“关系” 知识的总结 <1>:关系的基础概念 |
您所在的位置:网站首页 › 集合与函数有什么关系 › 离散数学知识点总结(10)“关系” 知识的总结 <1>:关系的基础概念 |
离散数学知识点总结(10)“关系” 知识的总结 <1>:关系的基础概念
文章目录
有序 n 元组和集合的笛卡尔积序偶关系有序二元组序偶相等有序三元组有序n元组有序 n 元组相等
集合的笛卡尔积集合笛卡尔积的性质
集合的二元关系及其表示方法相关关系的定义关系的定义域和值域关系的表示方法枚举法谓词公式法有向图法矩阵法
特殊的关系空关系
∅
\empty
∅全域关系(完全关系)恒等关系
关系的基本运算
关系的性质自反性反自反性对称性反对称性传递性
有序 n 元组和集合的笛卡尔积
序偶关系
有序二元组
有两个对象
x
,
y
x,y
x,y 组成的序列称为有序二元组,也称之为序偶,记作
<
x
,
y
>
序偶与集合不同,次序非常重要
序偶相等
设
<
x
,
y
>
,
<
u
,
v
>
,
, 是两个序偶,如果
x
=
u
且
y
=
v
x=u 且 y=v
x=u且y=v 那么这两个序偶被认为是相等的,记作
<
x
,
y
>
=
<
u
,
v
>
=
=
有序三元组
有序三元组是一个序偶,其第一个元素也是个序偶  因为第一个元素不是个序偶
有序n元组
有序n元组是一个序偶,其第一个元素本身是一个有序的 n-1 元组,记作
<
<
x
1
,
x
2
,
.
.
.
,
x
n
−
1
>
,
x
n
>
,简记为
<
x
1
,
x
2
,
.
.
.
,
x
n
−
1
,
x
n
>
有序 n 元组相等
因为第一个元素不是个序偶
有序n元组
有序n元组是一个序偶,其第一个元素本身是一个有序的 n-1 元组,记作
<
<
x
1
,
x
2
,
.
.
.
,
x
n
−
1
>
,
x
n
>
,简记为
<
x
1
,
x
2
,
.
.
.
,
x
n
−
1
,
x
n
>
有序 n 元组相等
A × B = { < x , y > ∣ x ∈ A ∧ y ∈ B } A×B=\{|x\in A \wedge y \in B\} A×B={∣x∈A∧y∈B} 集合的笛卡尔积不满足交换律集合的笛卡尔积也不满足结合律
  关系的定义
关系可以看做是 序偶的集合
关系的定义
关系可以看做是 序偶的集合   关系的定义域和值域
定义域就是关系集合
R
R
R 中的所有的第一元素
x
x
x 组成的集合值域就是 关系集合
R
R
R 中所有的 第二元素
y
y
y 组成的集合
关系的定义域和值域
定义域就是关系集合
R
R
R 中的所有的第一元素
x
x
x 组成的集合值域就是 关系集合
R
R
R 中所有的 第二元素
y
y
y 组成的集合   关系的表示方法
枚举法
谓词公式法
关系的表示方法
枚举法
谓词公式法
 恒等关系
恒等关系
 关系的性质
自反性反自反性对称性反对称性传递性
关系的性质
自反性反自反性对称性反对称性传递性
Note: 这里涉及到的所有的关系,都是某个集合和自身的关系,即集合 A A A,关系 R ⊆ A × A R \subseteq A×A R⊆A×A 自反性 有向图的每个节点都有指向自己的环矩阵的主对角线值都为 1   反自反性
有向图的每个节点都没有指向自己的环矩阵的主对角线值都为 0一个关系,不是 自反的,也不一定就是 反自反的
反自反性
有向图的每个节点都没有指向自己的环矩阵的主对角线值都为 0一个关系,不是 自反的,也不一定就是 反自反的   图中的
R
6
,
R
7
R_6,R_7
R6,R7 既不是自反关系,也不是反自反关系
对称性
有向图的不同节点之间 只要有边,就是方向相反的两条边矩阵特点:矩阵关于主对角线对称特别注意:恒等关系(主对角线全为1)、空关系(矩阵全为0) 都是 对称关系
图中的
R
6
,
R
7
R_6,R_7
R6,R7 既不是自反关系,也不是反自反关系
对称性
有向图的不同节点之间 只要有边,就是方向相反的两条边矩阵特点:矩阵关于主对角线对称特别注意:恒等关系(主对角线全为1)、空关系(矩阵全为0) 都是 对称关系   图中
R
4
,
R
8
R_4, R_8
R4,R8 分别是 恒等关系 和 空关系,他们都是对称关系
反对称性
有向图的不同节点之间 只要有边,最多只有一条单方向的边矩阵特点:矩阵关于主对角线对称的位置,最多只有一个 1对称关系和反对称关系不是完全对立的,有些对称关系,也同样是反对称关系
图中
R
4
,
R
8
R_4, R_8
R4,R8 分别是 恒等关系 和 空关系,他们都是对称关系
反对称性
有向图的不同节点之间 只要有边,最多只有一条单方向的边矩阵特点:矩阵关于主对角线对称的位置,最多只有一个 1对称关系和反对称关系不是完全对立的,有些对称关系,也同样是反对称关系
 传递性
通过有向图和矩阵不容易识别是否具有传递性,要通过传递性的定义来检查。
传递性
通过有向图和矩阵不容易识别是否具有传递性,要通过传递性的定义来检查。   R
1
R_1
R1 中,
x
R
y
xRy
xRy 为假,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此整个谓词公式为真,因此满足传递性。所以我们可以得到结论,独立无环的节点不影响传递性
R
2
R_2
R2 中,图中存在
x
R
x
xRx
xRx 因此
x
R
y
xRy
xRy 为假,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此依然满足传递性,所以我们得到另一个结论 独立有环的节点不影响传递性
R
3
R_3
R3 中,图中存在
x
R
x
xRx
xRx ,
x
R
y
xRy
xRy,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,依然满足传递性。
R
4
R_4
R4 中,图中存在
y
R
x
yRx
yRx 也有
x
R
x
xRx
xRx (可以把
y
R
x
yRx
yRx 和
x
R
x
xRx
xRx 看做是
x
R
y
,
y
R
z
xRy, yRz
xRy,yRz 的特殊情况),即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,而确实后件也确实为真,因为
x
R
x
xRx
xRx 确实存在,所以
R
4
R_4
R4 满足传递性
R
5
R_5
R5 中,图中存在
x
R
y
xRy
xRy , 不存在
y
R
z
yRz
yRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,依然满足传递性。
R
6
R_6
R6 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但不存在后件
x
R
x
xRx
xRx 因此不满足传递性。
R
7
R_7
R7 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,同时也存在后件为真
x
R
x
xRx
xRx 因此满足传递性。
R
8
R_8
R8 中,图中存在
x
R
y
xRy
xRy ,
x
R
z
xRz
xRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此满足传递性。
R
9
R_9
R9 中,图中存在
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但不存在后件
x
R
z
xRz
xRz 因此不满足传递性。
R
10
R_{10}
R10 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,也存在后件
x
R
z
xRz
xRz 因此满足传递性。
R
11
R_{11}
R11 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但后件为
z
R
x
zRx
zRx 因此后件为假,不满足传递性。此外,我们还可以推导出 空关系 和 恒等关系 以及 完全关系 也是满足传递性的
因为空关系就是三个独立的点,使得传递性的前件为假恒等关系就是三个独立的成环的点,也使得传递性的前件为假完全关系就是所有点之间的线都是双向的并且有自己成环,因此他的传递性关系判断的前件为真,后件也为真
R
1
R_1
R1 中,
x
R
y
xRy
xRy 为假,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此整个谓词公式为真,因此满足传递性。所以我们可以得到结论,独立无环的节点不影响传递性
R
2
R_2
R2 中,图中存在
x
R
x
xRx
xRx 因此
x
R
y
xRy
xRy 为假,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此依然满足传递性,所以我们得到另一个结论 独立有环的节点不影响传递性
R
3
R_3
R3 中,图中存在
x
R
x
xRx
xRx ,
x
R
y
xRy
xRy,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,依然满足传递性。
R
4
R_4
R4 中,图中存在
y
R
x
yRx
yRx 也有
x
R
x
xRx
xRx (可以把
y
R
x
yRx
yRx 和
x
R
x
xRx
xRx 看做是
x
R
y
,
y
R
z
xRy, yRz
xRy,yRz 的特殊情况),即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,而确实后件也确实为真,因为
x
R
x
xRx
xRx 确实存在,所以
R
4
R_4
R4 满足传递性
R
5
R_5
R5 中,图中存在
x
R
y
xRy
xRy , 不存在
y
R
z
yRz
yRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,依然满足传递性。
R
6
R_6
R6 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但不存在后件
x
R
x
xRx
xRx 因此不满足传递性。
R
7
R_7
R7 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,同时也存在后件为真
x
R
x
xRx
xRx 因此满足传递性。
R
8
R_8
R8 中,图中存在
x
R
y
xRy
xRy ,
x
R
z
xRz
xRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为假,因此满足传递性。
R
9
R_9
R9 中,图中存在
x
R
y
xRy
xRy ,
y
R
z
yRz
yRz,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但不存在后件
x
R
z
xRz
xRz 因此不满足传递性。
R
10
R_{10}
R10 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,也存在后件
x
R
z
xRz
xRz 因此满足传递性。
R
11
R_{11}
R11 中,图中存在
x
R
y
xRy
xRy ,
y
R
x
yRx
yRx,即
∀
x
∀
y
∀
z
(
(
x
∈
A
∧
y
∈
A
∧
z
∈
A
∧
x
R
y
∧
y
R
z
)
→
x
R
z
)
\forall x \forall y \forall z((x \in A \wedge y \in A \wedge z \in A \wedge xRy \wedge yRz) \rightarrow xRz)
∀x∀y∀z((x∈A∧y∈A∧z∈A∧xRy∧yRz)→xRz) 中的前件为真,但后件为
z
R
x
zRx
zRx 因此后件为假,不满足传递性。此外,我们还可以推导出 空关系 和 恒等关系 以及 完全关系 也是满足传递性的
因为空关系就是三个独立的点,使得传递性的前件为假恒等关系就是三个独立的成环的点,也使得传递性的前件为假完全关系就是所有点之间的线都是双向的并且有自己成环,因此他的传递性关系判断的前件为真,后件也为真
|
【本文地址】







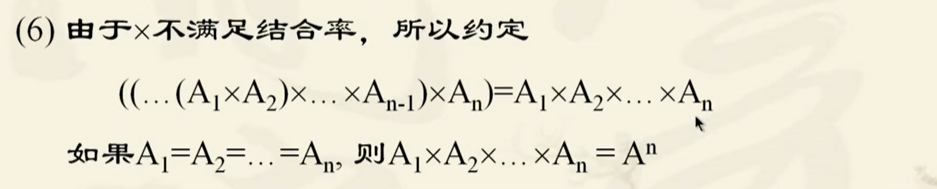


 - 第一个图表示的是在两个集合上的关系:在
A
,
B
A, B
A,B 上的关系
R
1
R_1
R1 - 第二种图表示的是一个集合和自身的关系:
A
,
A
A, A
A,A 的关系,
R
2
R_2
R2
- 第一个图表示的是在两个集合上的关系:在
A
,
B
A, B
A,B 上的关系
R
1
R_1
R1 - 第二种图表示的是一个集合和自身的关系:
A
,
A
A, A
A,A 的关系,
R
2
R_2
R2



