数据结构之图 |
您所在的位置:网站首页 › 逻辑结构关系图 › 数据结构之图 |
数据结构之图
|
一.图的基本概念 "多对多"逻辑关系数据的结构——图存储结构。 分类: 无向图:无向图中只有顶点和边说法,其中,图的度为每个顶点的度的和最后再除以二;相应表示两个顶点为 有向图中: 一条有向边成为弧,箭头指向一边为弧头,另一端为弧尾 .它的度就是入度和出度之和(指向它的边的边数和它指向别的顶点的边数之和);相应表示两个顶点为(a,b) 路径和回路: 就像上面常说的, 无论是无向图还是有向图,从一个顶点到另一顶点途径的所有顶点组成的序列(包含这两个顶点),称为一条路径。 如果路径中第一个顶点和最后一个顶点相同,则此路径称为"回路"(或"环")。 并且,若路径中各顶点都不重复,此路径又被称为"简单路径"; 同样,若回路中的顶点互不重复,此回路被称为"简单回路"(或简单环)。 子图: 指的是由图中一部分顶点和边构成的图,称为原图的子图。 完全图: 若图中各个顶点都与除自身外的其他顶点有关系,这样的无向图称为完全图(如图 4a))。 同时,满足此条件的有向图则称为有向完全图(图 4b))。 具有 n 个顶点的完全图,图中边的数量为 n(n-1)/2;而对于具有 n 个顶点的有向完全图,图中弧的数量为 n(n-1)。 稀疏图和稠密图: 这两种图是相对存在的,即如果图中具有很少的边(或弧),此图就称为"稀疏图";反之,则称此图为"稠密图"。 稀疏和稠密的判断条件是:e < nlogn,其中 e 表示图中边(或弧)的数量,n 表示图中顶点的数量。如果式子成立,则为稀疏图;反之为稠密图。稀疏图和稠密图 连通图: 图中有回路,任意两个点有边能到达,再详细介绍就是图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通着的. 强连通图:图中任意两个点都有直达的边. 图中边上带权值称为带权图,带权的连通图称为网络. 连通图就是连通分量,连通分量就是极大连通图,其中极小连通图就是数,路径=顶点数-1 二.存储结构: 邻接矩阵表示法: 无向图中:有连接为1,无连接为0;出度和入度相等. 通过二阶矩阵,可以直观地判断出各个顶点的度,为该行(或该列)非 0 值的和。例如,第一行有两个 1,说明 V1 有两个边,所以度为 2。 有向图中: 邻接表表示法(指针): 图的邻接表存储结构是一种顺序分配和链式分配相结合的存储结构。它包括两个部分:一部分是数组,另一部分是链表,数组用来每条单链表的表头,有数组的特性可知定位每条单链表的时间都是O(1)。 无向图: 有向图:通过指向的边来判断(出度) 逆邻接表,按照入度的方式来. 遍历: 深度优先遍历(DFS) 所谓深度优先搜索,是从图中的一个顶点出发,每次遍历当前访问顶点的临界点,一直到访问的顶点没有未被访问过的临界点为止。 然后采用依次回退的方式,查看来的路上每一个顶点是否有其它未被访问的临界点。 访问完成后,判断图中的顶点是否已经全部遍历完成,如果没有,以未访问的顶点为起始点,重复上述过程。 深度优先搜索是一个不断回溯的过程。 广度优先搜索(BFS) 广度优先搜索类似于树的层次遍历。 从图中的某一顶点出发,遍历每一个顶点时,依次遍历其所有的邻接点,然后再从这些邻接点出发,同样依次访问它们的邻接点。 按照此过程,直到图中所有被访问过的顶点的邻接点都被访问到。 最后还需要做的操作就是查看图中是否存在尚未被访问的顶点,若有,则以该顶点为起始点,重复上述遍历的过程。 还拿图 1 中的无向图为例,假设 V1 作为起始点,遍历其所有的邻接点 V2 和 V3 以 V2 为起始点,访问邻接点 V4 和 V5 以 V3 为起始点,访问邻接点 V6 、 V7 以 V4 为起始点访问 V8 以 V5 为起始点,由于 V5 所有的起始点已经全部被访问,所有直接略过 V6 和 V7 也是如此。 以 V1 为起始点的遍历过程结束后,判断图中是否还有未被访问的点,由于图 1 中没有了,所以整个图遍历结束。 遍历顶点的顺序为: V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> V8 三.最短路径(Dijkstra算法) 思路: 采用的是一种贪心的策略,从第一元素开始,看他有几条指向边,只是比较一条边,找到带权值最小的一条;二次是 两条边,通过最短的顶点再延伸出去所能到达的顶点,比对权值找到最小的一边以及顶点;往后依次类推,知道找到最后一个点,这时,所有的点都能找到一遍,从而找到第一个顶点到任意一点的最短路径.默认Dijkstra算法时间复杂度为 o(n^2). 演示:
既然是求 v1顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后,dis[2](下标从0开始)的值就已经从“估计值”变为了“确定值”,即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。 为什么呢?因为目前离 v1顶点最近的是 v3顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短. OK,既然确定了一个顶点的最短路径,下面我们就要根据这个新入的顶点V3会有出度,发现以v3 为弧尾的有: < v3,v4 >,那么我们看看路径:v1–v3–v4的长度是否比v1–v4短,其实这个已经是很明显的了,因为dis[3]代表的就是v1–v4的长度为无穷大,而v1–v3–v4的长度为:10+50=60,所以更新dis[3]的值,得到如下结果: 然后,我们又从除dis[2]和dis[0]外的其他值中寻找最小值,发现dis[4]的值最小,通过之前是解释的原理,可以知道v1到v5的最短距离就是dis[4]的值,然后,我们把v5加入到集合T中,然后,考虑v5的出度是否会影响我们的数组dis的值,v5有两条出度:< v5,v4>和 < v5,v6>,然后我们发现:v1–v5–v4的长度为:50,而dis[3]的值为60,所以我们要更新dis[3]的值.另外,v1-v5-v6的长度为:90,而dis[5]为100,所以我们需要更新dis[5]的值。更新后的dis数组如下图:
然后,继续从dis中选择未确定的顶点的值中选择一个最小的值,发现dis[3]的值是最小的,所以把v4加入到集合T中,此时集合T={v1,v3,v5,v4},然后,考虑v4的出度是否会影响我们的数组dis的值,v4有一条出度:< v4,v6>,然后我们发现:v1–v5–v4–v6的长度为:60,而dis[5]的值为90,所以我们要更新dis[5]的值,更新后的dis数组如下图: 然后,我们使用同样原理,分别确定了v6和v2的最短路径,最后dis的数组的值如下: 因此,从图中,我们可以发现v1-v2的值为:∞,代表没有路径从v1到达v2。所以我们得到的最后的结果为: *起点 终点 最短路径 长度 v1 v2 无 ∞ v3 {v1,v3} 10 v4 {v1,v5,v4} 50 v5 {v1,v5} 30 v6 {v1,v5,v4,v6} 60 * 转载:https://blog.csdn.net/qq_35644234/article/details/60870719 |
【本文地址】
今日新闻 |
推荐新闻 |
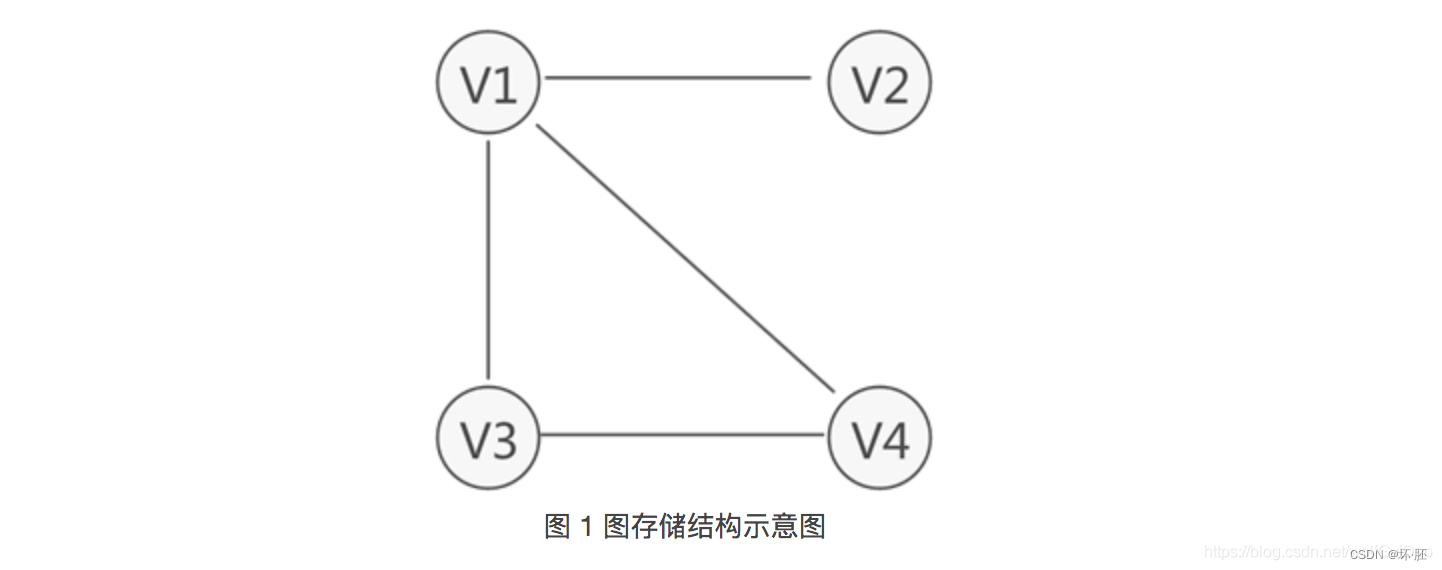 图中含有 4 个顶点,分别为顶点 V1、V2、V3 和 V4。 集合为 V={V1,V2,V3,V4}。这里图中v1可以到达v2,v2也可以达到v1,其他结点依次.
图中含有 4 个顶点,分别为顶点 V1、V2、V3 和 V4。 集合为 V={V1,V2,V3,V4}。这里图中v1可以到达v2,v2也可以达到v1,其他结点依次.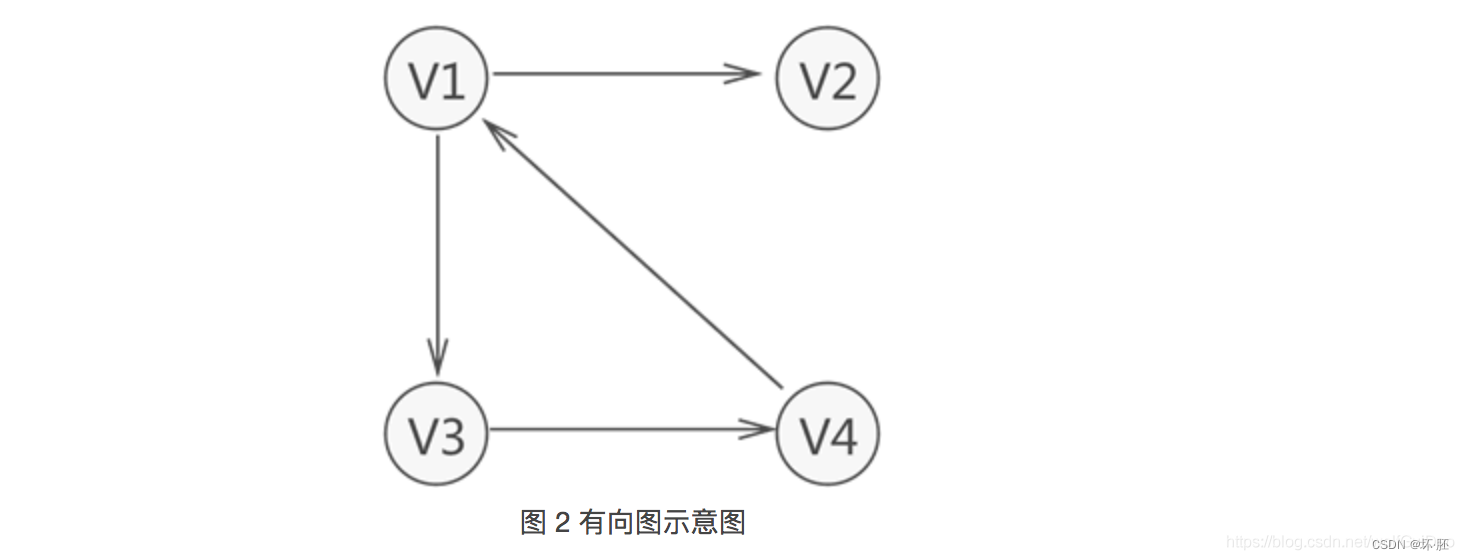 可以看到,各个顶点之间的关系并不是"双向"的。比如,V4 只与 V1 存在联系(从 V4 可直接找到 V1),而与 V3 没有直接联系;同样,V3 只与 V4 存在联系(从 V3 可直接找到 V4),而与 V1 没有直接联系,以此类推。 其中,又可以衍生出弧和度: 弧: 有向图中,无箭头一端的顶点通常被称为"初始点"或"弧尾",箭头直线的顶点被称为"终端点"或"弧头"。 入度和出度: 对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V)); 箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V)) 上图顶点 V1,该顶点的入度为 1,出度为 2(该顶点的度为 3)。
可以看到,各个顶点之间的关系并不是"双向"的。比如,V4 只与 V1 存在联系(从 V4 可直接找到 V1),而与 V3 没有直接联系;同样,V3 只与 V4 存在联系(从 V3 可直接找到 V4),而与 V1 没有直接联系,以此类推。 其中,又可以衍生出弧和度: 弧: 有向图中,无箭头一端的顶点通常被称为"初始点"或"弧尾",箭头直线的顶点被称为"终端点"或"弧头"。 入度和出度: 对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V)); 箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V)) 上图顶点 V1,该顶点的入度为 1,出度为 2(该顶点的度为 3)。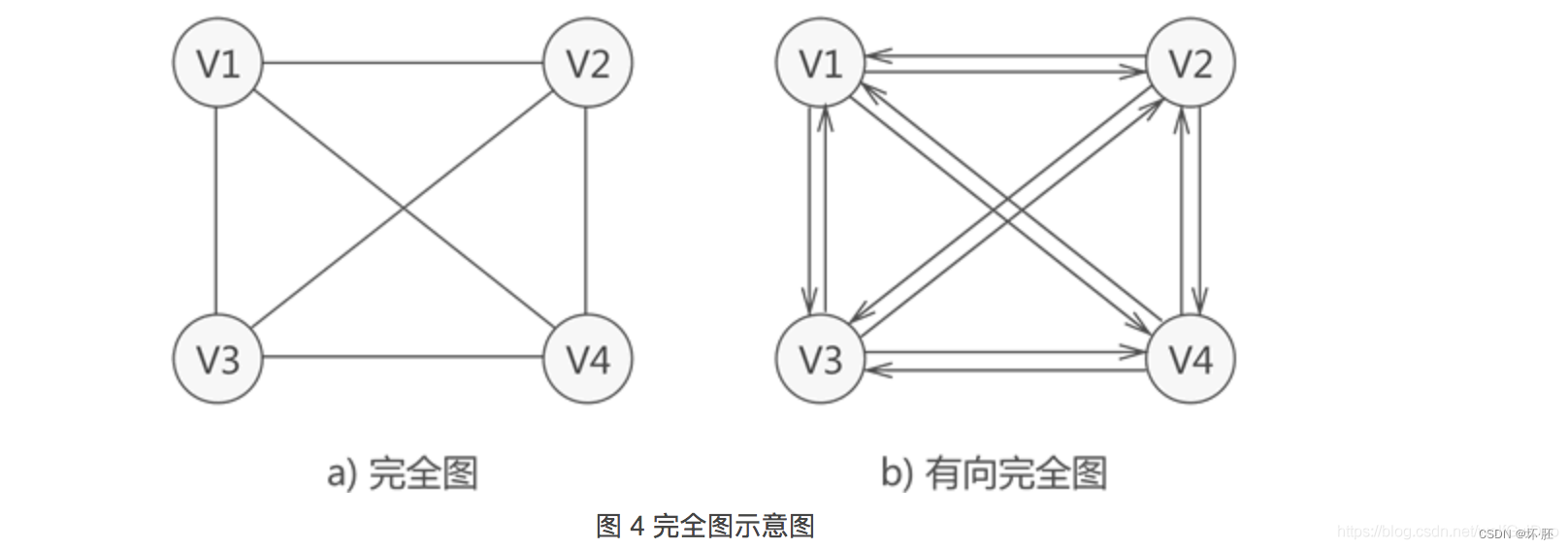
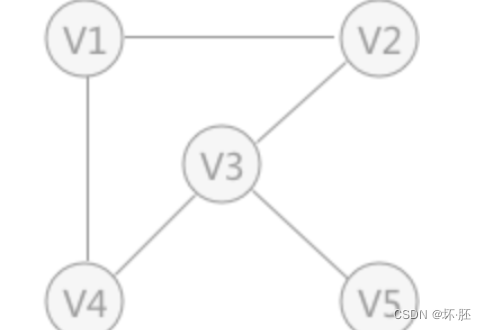
 对于无向图来说,二维数组构建的二阶矩阵,实际上是对称矩阵,在存储时就可以采用压缩存储的方式存储下三角或者上三角。
对于无向图来说,二维数组构建的二阶矩阵,实际上是对称矩阵,在存储时就可以采用压缩存储的方式存储下三角或者上三角。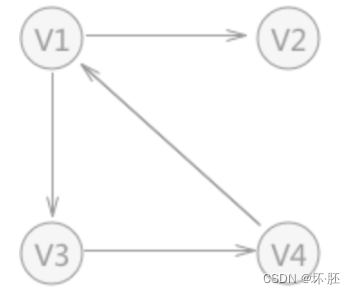
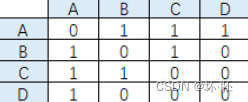
 arcs[0][1] = 1 ,证明从 V1 到 V2 有弧存在。 这里要说明的是,如果是带权值的话,1的位置该为权值,0的位置可以换为无穷,也可以为0. 且通过二阶矩阵,可以很轻松得知各顶点的出度和入度,出度为该行非 0 值的和,入度为该列非 0 值的和。 例如,V1 的出度为第一行两个 1 的和,为 2 ; V1 的入度为第一列中 1 的和,为 1 。所以 V1 的出度为 2 ,入度为 1 ,度为两者的和 3
arcs[0][1] = 1 ,证明从 V1 到 V2 有弧存在。 这里要说明的是,如果是带权值的话,1的位置该为权值,0的位置可以换为无穷,也可以为0. 且通过二阶矩阵,可以很轻松得知各顶点的出度和入度,出度为该行非 0 值的和,入度为该列非 0 值的和。 例如,V1 的出度为第一行两个 1 的和,为 2 ; V1 的入度为第一列中 1 的和,为 1 。所以 V1 的出度为 2 ,入度为 1 ,度为两者的和 3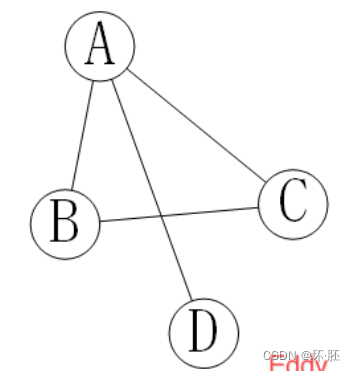
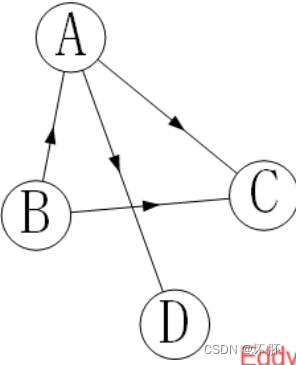 出度的邻接表:
出度的邻接表: 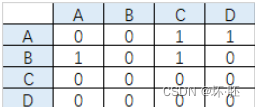 逆邻接表:
逆邻接表: 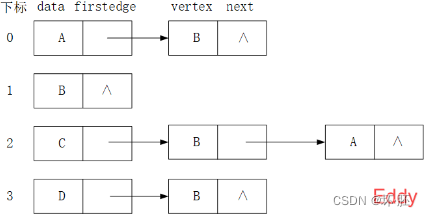
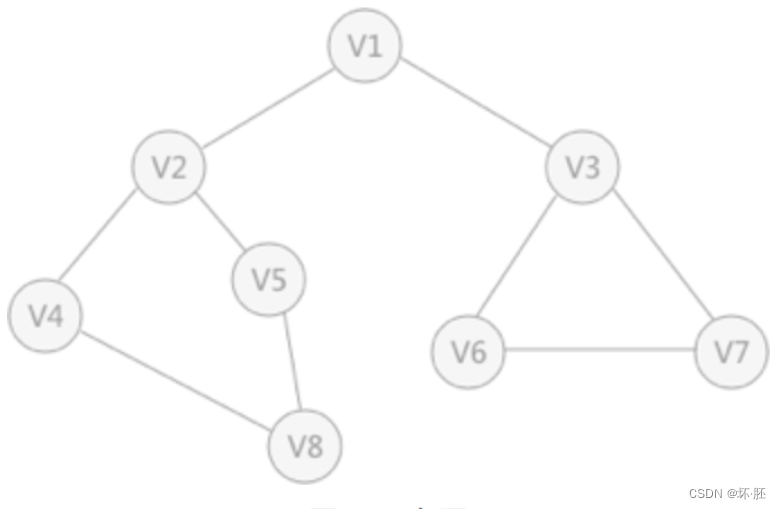 深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。例如图 1 是一个无向图,采用深度优先算法遍历这个图的过程为: 首先任意找一个未被遍历过的顶点,例如从 V1 开始,由于 V1 率先访问过了,所以,需要标记 V1 的状态为访问过; 然后遍历 V1 的邻接点,例如访问 V2 ,并做标记,然后访问 V2 的邻接点,例如 V4 (做标记),然后 V8 ,然后 V5 ; 当继续遍历 V5 的邻接点时,根据之前做的标记显示,所有邻接点都被访问过了。 此时,从 V5 回退到 V8 ,看 V8 是否有未被访问过的邻接点,如果没有,继续回退到 V4 , V2 , V1 ; 通过查看 V1 ,找到一个未被访问过的顶点 V3 ,继续遍历,然后访问 V3 邻接点 V6 ,然后 V7 ; 由于 V7 没有未被访问的邻接点,所有回退到 V6 ,继续回退至 V3 ,最后到达 V1 ,发现没有未被访问的; 最后一步需要判断是否所有顶点都被访问,如果还有没被访问的,以未被访问的顶点为第一个顶点,继续依照上边的方式进行遍历。 根据上边的过程,可以得到图 1 通过深度优先搜索获得的顶点的遍历次序为: V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7
深度优先搜索的过程类似于树的先序遍历,首先从例子中体会深度优先搜索。例如图 1 是一个无向图,采用深度优先算法遍历这个图的过程为: 首先任意找一个未被遍历过的顶点,例如从 V1 开始,由于 V1 率先访问过了,所以,需要标记 V1 的状态为访问过; 然后遍历 V1 的邻接点,例如访问 V2 ,并做标记,然后访问 V2 的邻接点,例如 V4 (做标记),然后 V8 ,然后 V5 ; 当继续遍历 V5 的邻接点时,根据之前做的标记显示,所有邻接点都被访问过了。 此时,从 V5 回退到 V8 ,看 V8 是否有未被访问过的邻接点,如果没有,继续回退到 V4 , V2 , V1 ; 通过查看 V1 ,找到一个未被访问过的顶点 V3 ,继续遍历,然后访问 V3 邻接点 V6 ,然后 V7 ; 由于 V7 没有未被访问的邻接点,所有回退到 V6 ,继续回退至 V3 ,最后到达 V1 ,发现没有未被访问的; 最后一步需要判断是否所有顶点都被访问,如果还有没被访问的,以未被访问的顶点为第一个顶点,继续依照上边的方式进行遍历。 根据上边的过程,可以得到图 1 通过深度优先搜索获得的顶点的遍历次序为: V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7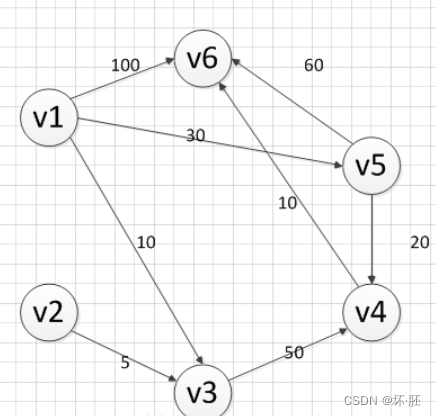 首先第一步,我们先声明一个dis数组,该数组初始化的值为:
首先第一步,我们先声明一个dis数组,该数组初始化的值为: 我们的顶点集T的初始化为:T={v1}
我们的顶点集T的初始化为:T={v1} 在这里插入图片描述 因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。
在这里插入图片描述 因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。

