在求解最优化问题中，线搜索是一类非常重要的迭代算法。线搜索的迭代过程是 xk+1=xk+αkpk 。其中 αk 和 pk 分别表示搜索步长和搜索方向，因此线搜索需要解决如何求解步长和确定搜索方向，该小结主要介绍 1. 步长 αk 的选择 2. 步长的实现算法 2. 线搜索的收敛性 3. 牛顿方法的优化

根据迭代算法 xk+1=xk+αkpk ，根据之前的介绍搜索方向 pk 需要满足，它是一个下降方向，即满足 ∇fkpk≤0 ，则 pk=−B−1k∇fk ，B为对称非奇异矩阵，根据 Bk 的选择会产生以下几个方向: 1. Bk=I 时，搜索方向为负梯度方向，该方法为最速下降方向。 2. Bk=∇2fk 时，该方法为牛顿方法。 3. Bk 需要满足对称正定矩阵，该方法为拟牛顿方法。 当搜索方向确定后，下一步就要确定步长。

求解步长需要解决的一个最优化问题是，在确定了下降方向 pk 后，求解一个一元最优化问题

对于一个一元二次问题，最优解形式为 ∇Tf(xk+αpk)pk=0 ，即 ∇Tfk+1pk=0

性质：对于最速下降法，当选择最优步长时，每一步的搜索方向和上一步是正交的，即 pTk+1pk=0

证明：由于当选择为最优步长时满足 ∇Tfk+1pk=0 。因此性质成立， pk+1=−∇fTk+1

非精确算法的思路就是寻找步长 α 的一个区间，通过逐步二分的方法去寻找满足条件的点。当搜索结束时，需要满足该步长能够对目标函数带来充分的减少。为提高非精确算法的搜索效率， α 需要满足一定的条件。

Armijo是一个相对比较简单的条件，即目标函数需要充分小。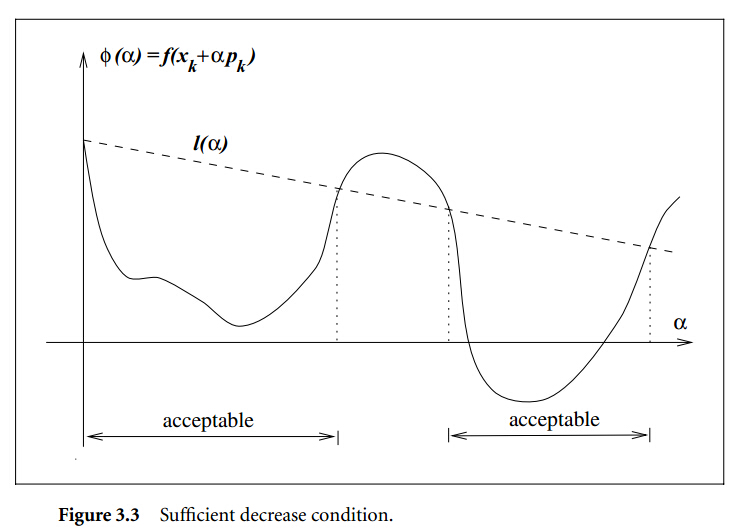

Curvature条件是指：