[计算机数值分析]埃特金算法加速迭代法求根过程 |
您所在的位置:网站首页 › 迭代c语言 › [计算机数值分析]埃特金算法加速迭代法求根过程 |
[计算机数值分析]埃特金算法加速迭代法求根过程
|
Spring-_-Bear 的 CSDN 博客导航
由于 前有加速方案 需要提供迭代函数 φ ( x ) φ(x) φ(x) 的导数 φ ′ ( x ) φ'(x) φ′(x) 而不便于实际应用。 若将迭代值 x ‾ k + 1 \overline{x}_{k+1} xk+1 = φ ( x k ) \varphi(x_{k}) φ(xk) 再迭代一次,得 x ~ k + 1 = φ ( x ‾ k + 1 ) \widetilde{x}_{k+1}=\varphi{(\overline{x}_{k+1})} x k+1=φ(xk+1) 由于 x ∗ − x ~ k + 1 ≈ L ( x ∗ − x ‾ k + 1 ) x^{*}-\widetilde{x}_{k+1}\approx L(x^{*}-\overline{x}_{k+1}) x∗−x k+1≈L(x∗−xk+1) 将其与 x ∗ − x ‾ k + 1 ≈ L ( x ∗ − x k ) x^{*} - \overline{x}_{k+1} \approx L(x^{*}-x_{k}) x∗−xk+1≈L(x∗−xk) 联立,消去未知的 L,有 x ∗ − x ‾ k + 1 x ∗ − x ~ k + 1 ≈ x ∗ − x k x ∗ − x ‾ k + 1 \frac{x^{*}-\overline{x}_{k+1}}{x^{*}-\widetilde{x}_{k+1}}\approx\frac{x^{*}-x_{k}}{x^{*}-\overline{x}_{k+1}} x∗−x k+1x∗−xk+1≈x∗−xk+1x∗−xk 由此得 x ∗ ≈ x ~ k + 1 − ( x ~ k + 1 − x ‾ k + 1 ) 2 x ~ k + 1 − 2 x ‾ k + 1 + x k x^{*}\approx\widetilde{x}_{k+1}-\frac{(\widetilde{x}_{k+1}-\overline{x}_{k+1})^{2}}{\widetilde{x}_{k+1}-2\overline{x}_{k+1}+x_{k}} x∗≈x k+1−x k+1−2xk+1+xk(x k+1−xk+1)2 若以上式右端得出得结果作为新的改进值,则这样构造出得加速公式不再含有关于导数的信息,但它需要使用两次迭代值进行加工。其具体计算公式如下: 迭代 x ‾ k + 1 \overline{x}_{k+1} xk+1 = φ ( x k ) \varphi(x_{k}) φ(xk)迭代 x ~ k + 1 = φ ( x ‾ k + 1 ) \widetilde{x}_{k+1}=\varphi{(\overline{x}_{k+1})} x k+1=φ(xk+1)改进 x k + 1 = x ~ k + 1 − ( x ~ k + 1 − x ‾ k + 1 ) 2 x ~ k + 1 − 2 x ‾ k + 1 + x k x_{k+1}=\widetilde{x}_{k+1}-\frac{(\widetilde{x}_{k+1}-\overline{x}_{k+1})^{2}}{\widetilde{x}_{k+1}-2\overline{x}_{k+1}+x_{k}} xk+1=x k+1−x k+1−2xk+1+xk(x k+1−xk+1)2上述方法称为埃特金(Aitken)加速方法。 使用埃特金加速算法解前例 求方程 x 3 − x − 1 = 0 x^{3} -x-1=0 x3−x−1=0 的唯一正根,如下图所示,埃特金算法的加速效果是显著的。 运行示例: 未使用加速算法,需要迭代 9 次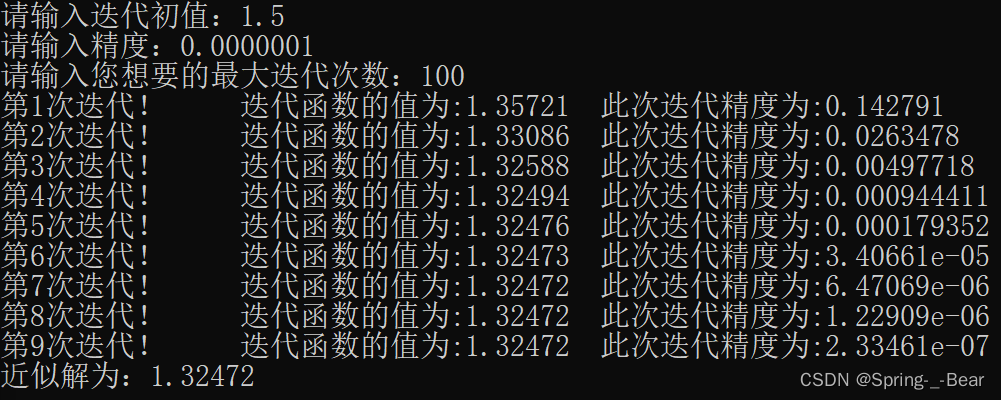 使用普通加速算法,需要迭代 4 次 使用普通加速算法,需要迭代 4 次 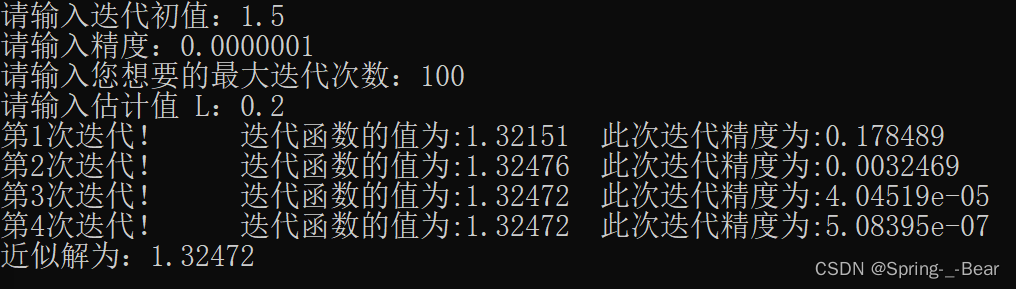 使用埃特金加速算法,仅需迭代 2 次 使用埃特金加速算法,仅需迭代 2 次 
程序源码: #include #include using namespace std; /** * f(x) = (x+1)^{1/3) */ double f(double x) { return pow(x + 1, 1.0 / 3); } int main(void) { double x0; cout x0; double accrucy; cout accrucy; int n; cout n; double x3; int count = 0; do { double x1 = f(x0); double x2 = f(x1); // x3 为利用埃特金加速公式处理后的近似解 x3 = x2 - pow(x2 - x1, 2) / (x2 - 2 * x1 + x0); if (abs(x0 - x3) cout |
【本文地址】