Python轴承故障诊断 (二)连续小波变换CWT |
您所在的位置:网站首页 › 轴承图样 › Python轴承故障诊断 (二)连续小波变换CWT |
Python轴承故障诊断 (二)连续小波变换CWT
|
目录 前言 1 连续小波变换CWT原理介绍 1.1 CWT概述 1.2 CWT的原理和本质 2 基于Python的CWT实现与参数对比 2.1 代码示例 2.2 参数介绍和选择策略 2.2.1 尺度长度: 2.2.2 小波函数(wavelet): 2.3 凯斯西储大学轴承数据的加载 2.4 CWT与参数选择对比 2.4.1 基于尺度为128,选择内圈数据比较 CWT 的不同小波函数 2.4.2 根据正常数据和三种故障数据,对比不同小波函数的辨识度 2.4.3 基于'cmor1.5-2'小波,选择滚珠故障数据比较 CWT 的不同尺度的变化:32、64、128、256; 3 基于时频图像的轴承故障诊断分类 3.1 生成时频图像数据集 3.2 定义数据加载器和VGG网络模型  往期精彩内容:
往期精彩内容:
Python-凯斯西储大学(CWRU)轴承数据解读与分类处理 Python轴承故障诊断 (一)短时傅里叶变换STFT Python轴承故障诊断 (二)连续小波变换CWT_pyts 小波变换 故障-CSDN博客 Python轴承故障诊断 (三)经验模态分解EMD_轴承诊断 pytorch-CSDN博客 Pytorch-LSTM轴承故障一维信号分类(一)_cwru数据集pytorch训练-CSDN博客 Pytorch-CNN轴承故障一维信号分类(二)-CSDN博客 Pytorch-Transformer轴承故障一维信号分类(三)-CSDN博客 Python轴承故障诊断 (四)基于EMD-CNN的故障分类-CSDN博客 Python轴承故障诊断 (五)基于EMD-LSTM的故障分类-CSDN博客 Python轴承故障诊断 (六)基于EMD-Transformer的故障分类-CSDN博客 Python轴承故障诊断 (七)基于EMD-CNN-LSTM的故障分类-CSDN博客 Python轴承故障诊断 (八)基于EMD-CNN-GRU并行模型的故障分类-CSDN博客 基于FFT + CNN - BiGRU-Attention 时域、频域特征注意力融合的轴承故障识别模型-CSDN博客 基于FFT + CNN - Transformer 时域、频域特征融合的轴承故障识别模型-CSDN博客 大甩卖-(CWRU)轴承故障诊数据集和代码全家桶-CSDN博客 Python轴承故障诊断 (九)基于VMD+CNN-BiLSTM的故障分类-CSDN博客 Python轴承故障诊断 (十)基于VMD+CNN-Transfromer的故障分类-CSDN博客 Python轴承故障诊断 (11)基于VMD+CNN-BiGRU-Attenion的故障分类-CSDN博客 交叉注意力融合时域、频域特征的FFT + CNN -BiLSTM-CrossAttention轴承故障识别模型-CSDN博客 交叉注意力融合时域、频域特征的FFT + CNN-Transformer-CrossAttention轴承故障识别模型-CSDN博客 轴承故障诊断 (12)基于交叉注意力特征融合的VMD+CNN-BiLSTM-CrossAttention故障识别模型-CSDN博客 Python轴承故障诊断入门教学-CSDN博客 Python轴承故障诊断 (13)基于故障信号特征提取的超强机器学习识别模型-CSDN博客 Python轴承故障诊断 (14)高创新故障识别模型-CSDN博客 Python轴承故障诊断 (15)基于CNN-Transformer的一维故障信号识别模型-CSDN博客 前言本文基于凯斯西储大学(CWRU)轴承数据,进行连续小波变换的介绍与参数选择,最后通过Python实现对故障数据的时频图像分类。凯斯西储大学轴承数据的详细介绍可以参考下文: Python-凯斯西储大学(CWRU)轴承数据解读与分类处理 短时傅里叶变换STFT可以参考如下: Python轴承故障诊断 (一)短时傅里叶变换STFT 前期内容介绍了短时傅里叶变换(STFT),在其一定程度上改善了傅里叶变换(FT) 无时间局部化能力的不足,但仍然存在以下不足: 在STFT中,选择了固定的时间窗,时间和频率的分辨率就保持不变; 由于STFT的基础是傅里叶变换,所以它不适合于分析非平稳信号,可用于分析平稳信号和准平稳信号。 轴承故障数据的信号特性常随时间变化,对于这种非平稳信号分析,CWT 提供了一种同时在时间和频率上定位信号特征的方法。 1 连续小波变换CWT原理介绍 1.1 CWT概述连续小波变换(Continuous Wavelet Transform,CWT)是一种用于在时域和频域上同时分析信号的方法,它通过使用不同尺度和位置的小波函数对信号进行变换,以获取信号的局部特性。 CWT的公式表示为:
其中,
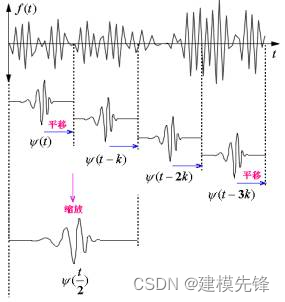
信号x(t)经过小波变换后,得到的结果是小波系数C,小波系数C是尺度a和位置b的函数。从物理意义上讲,小波系数C中蕴含着信号在各个尺度a和位置b上的信息[1]。 不同尺度和位置下小波的形状变换如图所示:
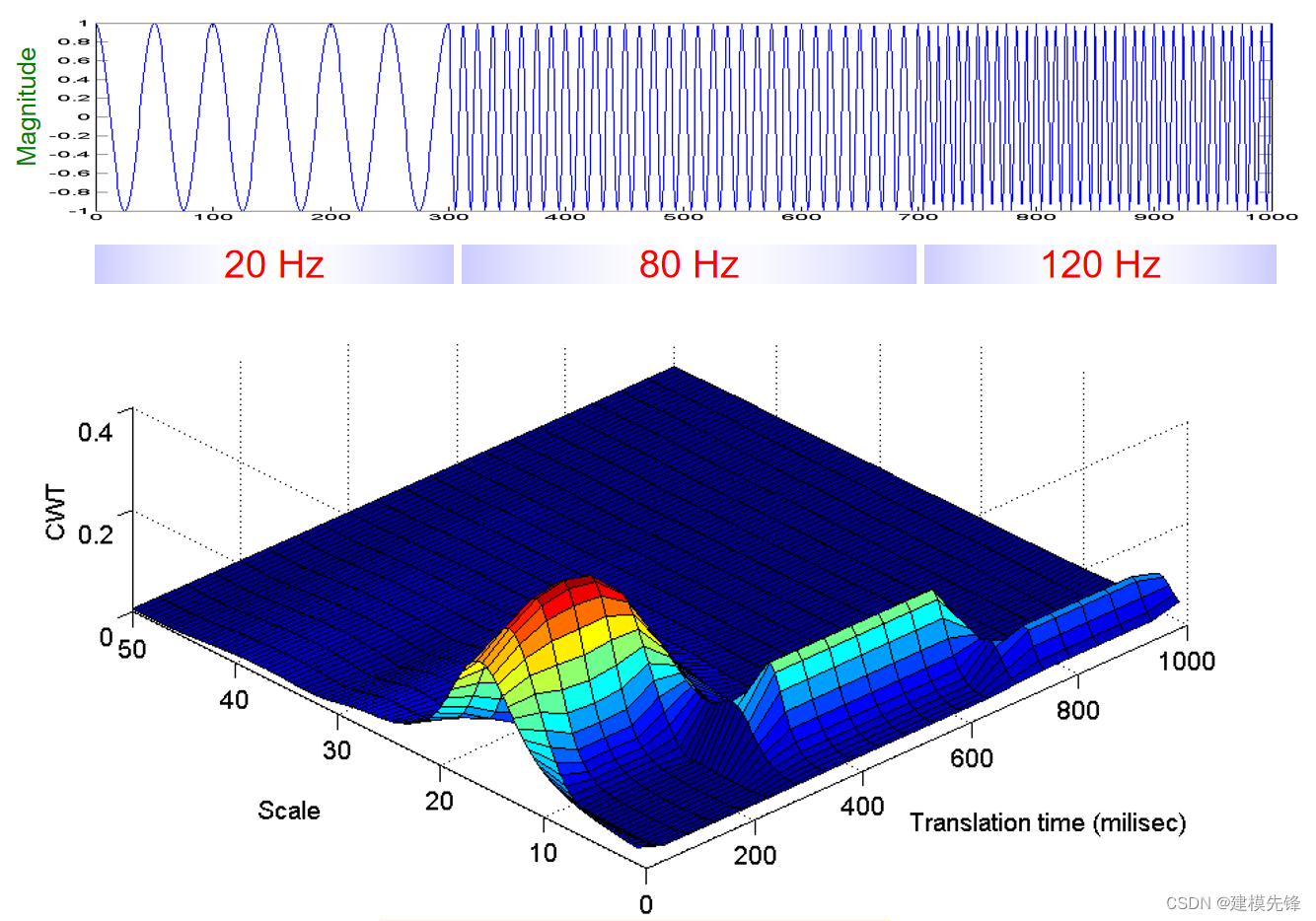
CWT的核心思想是在不同尺度(频率)和位置上对信号进行小波分解。为了达到这个目的,CWT使用一个小波函数(wavelet),通常称为母小波或基本小波。这个小波函数是一个可调整尺度的波形。 尺度和平移: CWT使用可调整尺度的小波函数,这个尺度参数决定了小波的频率,同时也使用平移参数,控制小波在时间轴上的位置。 小波函数: 小波函数通常称为母小波,是一种局部化的波形,通过缩放和平移,可以适应信号的不同频率和位置。 卷积过程: CWT通过在不同尺度和位置上对信号进行小波函数的卷积,生成一系列的小波系数。 1.3 时频图谱 连续小波变换的结果是小波系数,提供了信号在时间和频率上的局部信息。这些小波系数构成了时频平面上的图像,被称为时频图谱。时频图谱显示了信号在时间和频率上的局部特性。这对于定位故障信号中的异常事件以及了解信号的时频结构非常有用。
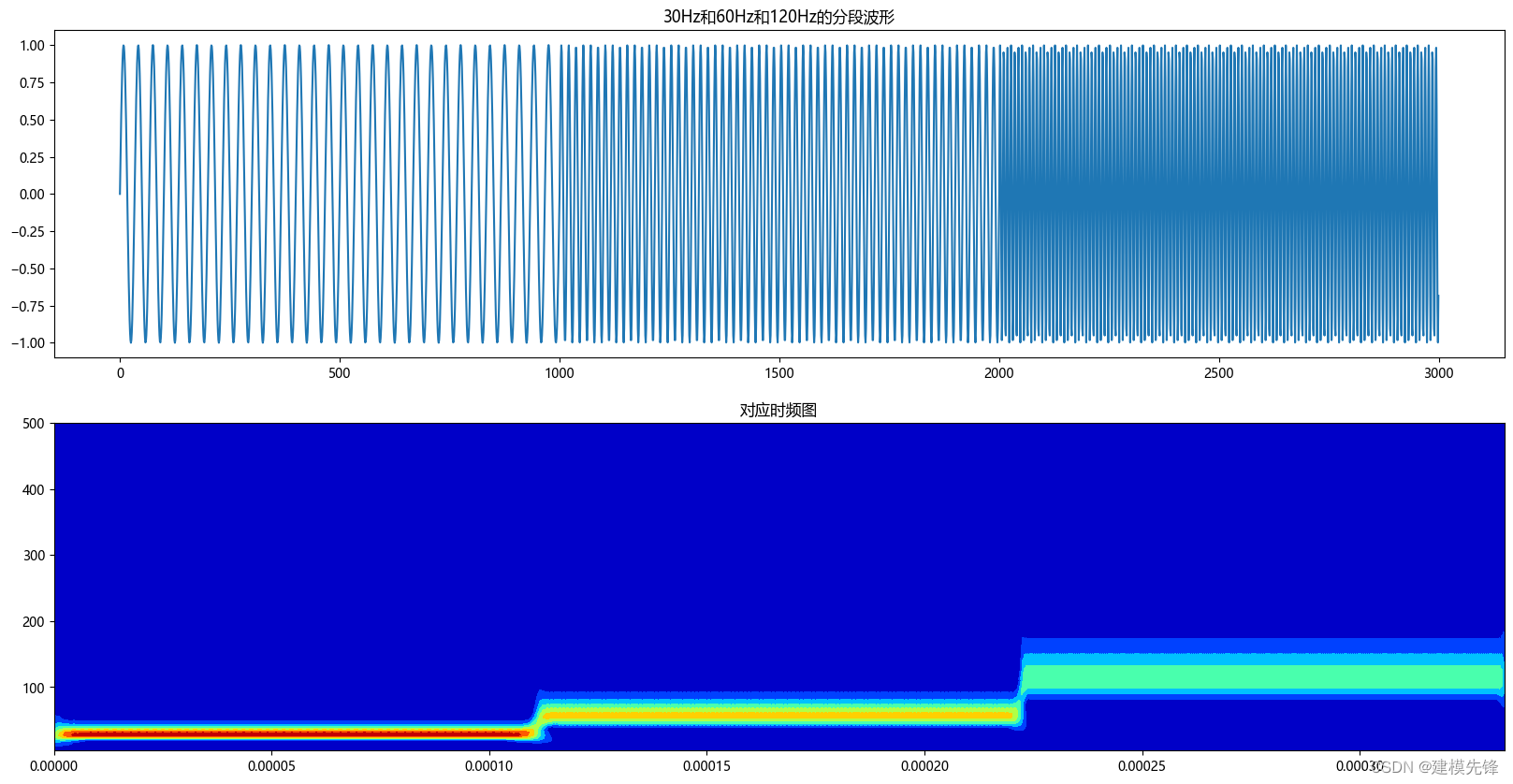
在 Python 中,使用 pywt 库来实现连续小波变换(CWT) 2.1 代码示例 import numpy as np import matplotlib.pyplot as plt import pywt # 生成三个不同频率成分的信号 3000个点 fs = 1000 # 采样率 time = np.linspace(0, 1, fs, endpoint=False) # 时间 # 第一个频率成分 signal1 = np.sin(2 * np.pi * 30 * time) # 第二个频率成分 signal2 = np.sin(2 * np.pi * 60 * time) # 第三个频率成分 signal3 = np.sin(2 * np.pi * 120 * time) # 合并三个信号 signal = np.concatenate((signal1, signal2, signal3)) # 连续小波变换参数 # 采样频率 sampling_rate = 3000 # 尺度长度 totalscal = 128 # 小波基函数 wavename = 'morl' # 小波函数中心频率 fc = pywt.central_frequency(wavename) # 常数c cparam = 2 * fc * totalscal # 尺度序列 scales = cparam / np.arange(totalscal, 0, -1) # 进行CWT连续小波变换 coefficients, frequencies = pywt.cwt(signal, scales, wavename, 1.0/1000) # 小波系数矩阵绝对值 amp = abs(coefficients) # 根据采样频率 sampling_period 生成时间轴 t t = np.linspace(0, 1.0/sampling_rate, sampling_rate, endpoint=False) # 绘制时频图谱 plt.figure(figsize=(20,10)) plt.subplot(2,1,1) plt.plot(signal) plt.title('30Hz和60Hz和120Hz的分段波形') plt.subplot(2,1,2) plt.contourf(t, frequencies, amp, cmap='jet') plt.title('对应时频图') plt.show()参数解释 totalscal:表示尺度长度,表征频率的参数,选择不同的尺度可以捕捉信号不同尺度上的特征; wavename:表示小波函数的类型,不同的小波适用于不同类型的信号; fc:表示小波函数的中心频率,小波函数在频率域中有一个中心频率;这个中心频率是与小波函数形状和性质有关的一个重要参数; scales:表示尺度序列,CWT本质上是将你的信号与不同尺度的小波进行相关,scales 参数确定尺度范围; coefficients:表示信号变换后的小波系数; frequencies :表示对应的频率信息
在连续小波变换(CWT)中,尺度参数是一个关键的选择,因为它决定了小波函数的宽度,从而影响了频率分辨率。尺度与频率成反比,尺度反映了分析的频率范围,尺度越小,小波函数衰减越快,频率越高;尺度越大,小波函数衰减越慢,频率越低[1]。
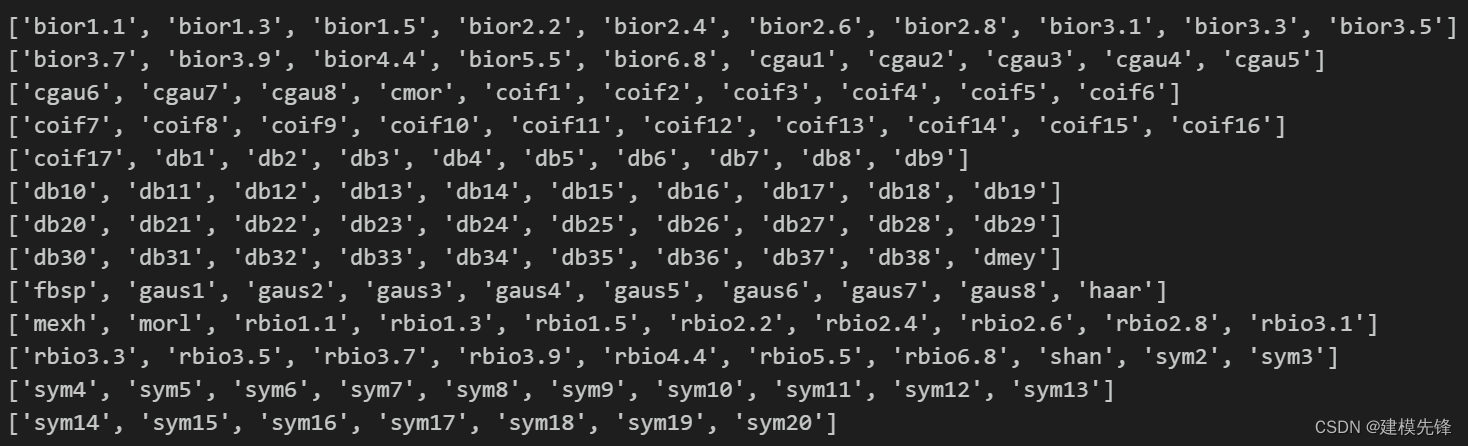
选择小波尺度的一般原则是: 高频特征: 如果关注信号的高频特征,应该选择较小的尺度; 低频特征: 如果关注信号的低频特征,应该选择较大的尺度; 覆盖感兴趣的频率范围: 尺度参数的选择应该使小波函数能够覆盖感兴趣的频率范围;如果期望信号有很高的频率变化,可能需要选择较小的尺度; 频率分辨率: 较小的尺度提供更好的频率分辨率,因为小波函数较窄,可以更精细地定位频率;但是,这也意味着在时间上的分辨率较差,因此,需要权衡时间分辨率和频率分辨率; 信号持续时间: 尺度参数的选择还应考虑信号的持续时间,如果信号是短暂的,可能需要较小的尺度; 尺度间隔: 在尺度参数上选择合适的间隔,以确保在整个频率范围内进行了适当的采样;这取决于具体的应用和信号特性。 2.2.2 小波函数(wavelet):小波函数(wavelet)的选择也连续小波变换中的一个重要参数,它决定了小波基函数的形状,不同的小波函数适用于不同类型的信号和应用。 打印 Python pywt 包中的所有小波函数类型: import pywt # 获取小波函数列表 wavelets = pywt.wavelist() # 打印小波函数列表 # 按照12行,10列的形式打印数据 num_rows = 12 num_columns = 10 for i in range(0, len(wavelets), num_columns): row = wavelets[i:i + num_columns] print(row)
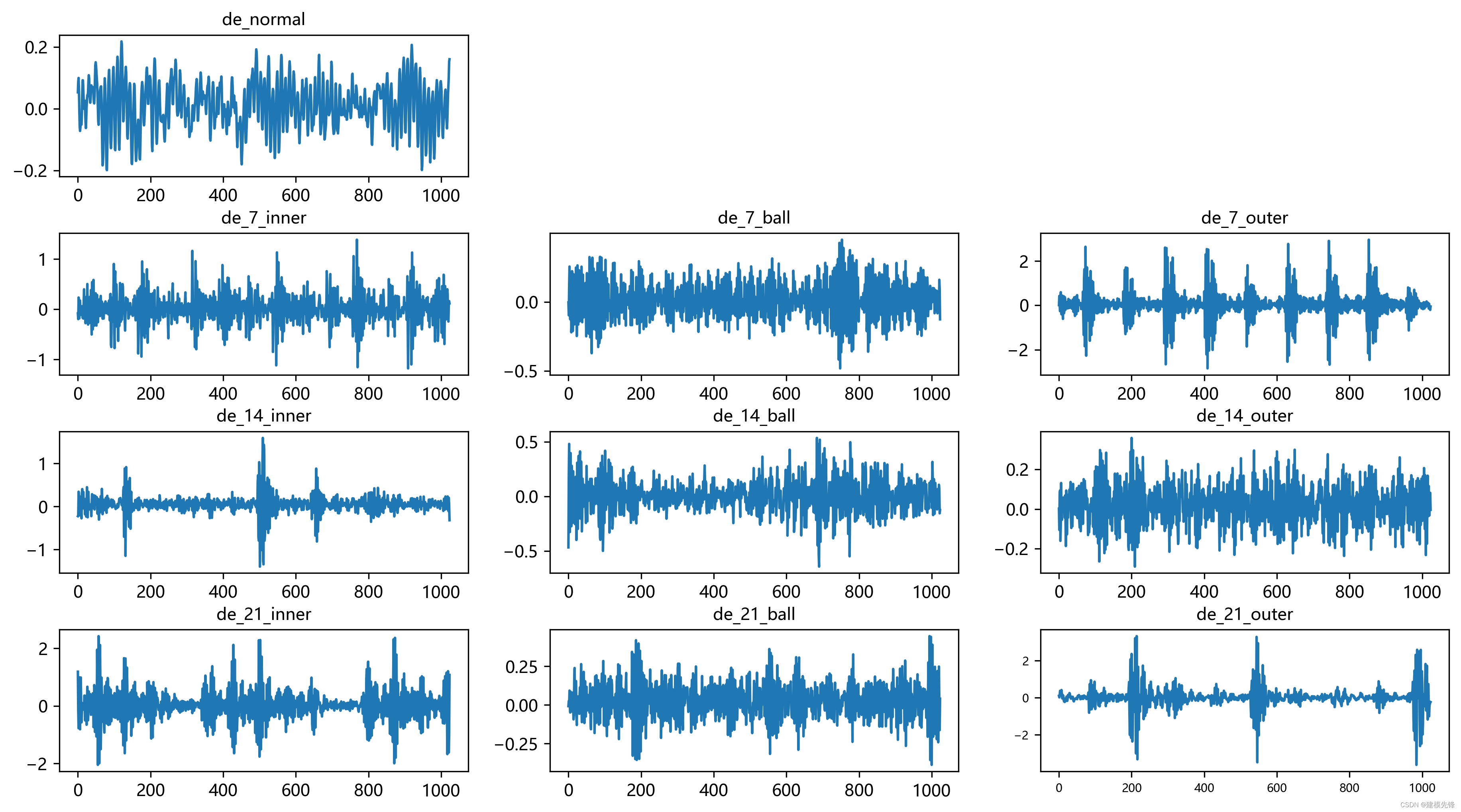
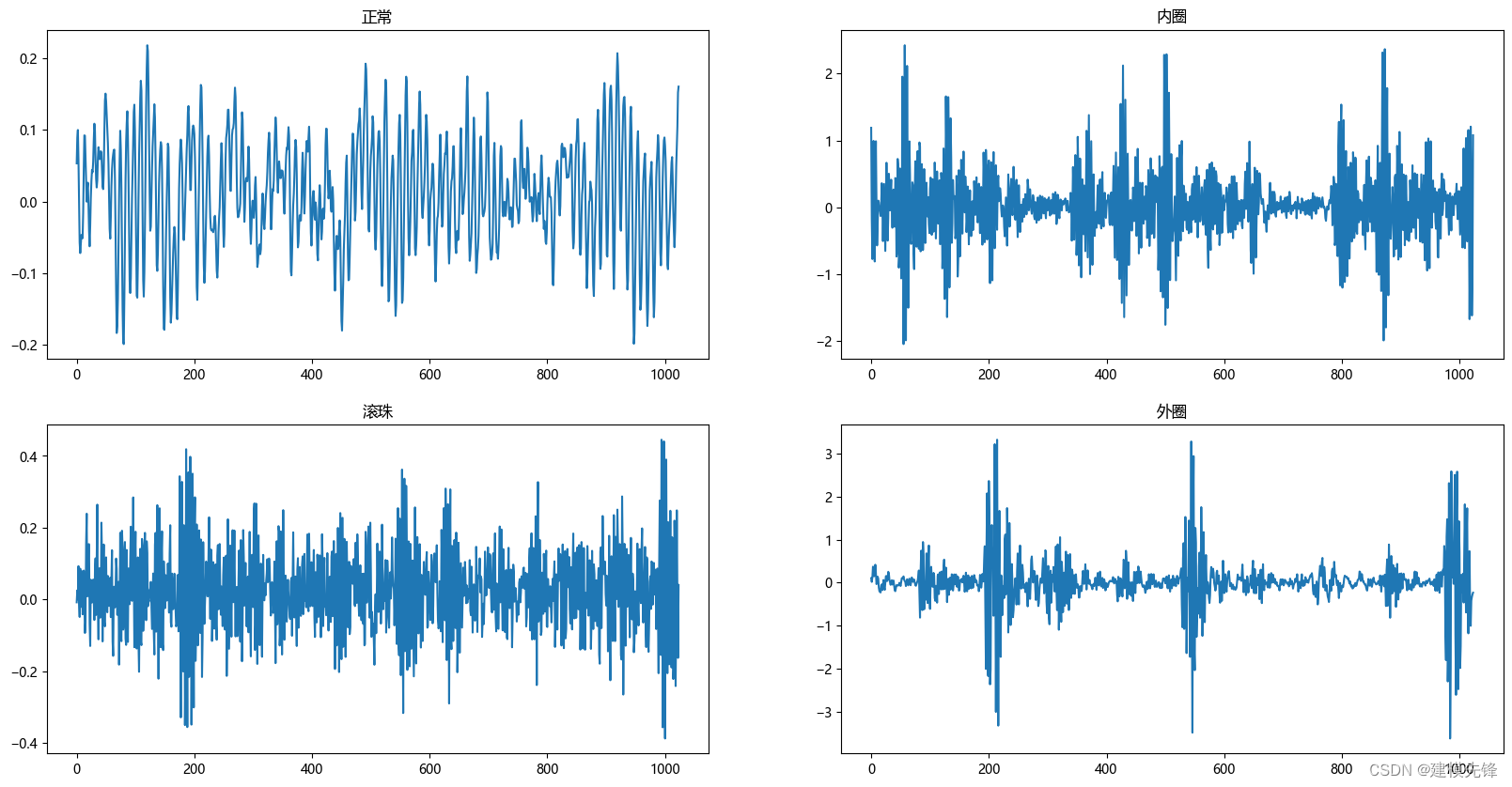
介绍常用的小波基函数: 'morl' :Morlet小波是一种复杂的小波函数,它在频率域和时域都有较好的局部化性质;Morlet小波通常用于处理时频局部化要求较高的信号,比如处理振动信号或某些生物医学信号; 'cmor': Complex Morlet wavelet,复数 Morlet 小波,是 Morlet 小波的一个变种; 'cgau' :Complex Gaussian wavelet,复数高斯小波,用于近似高斯信号; 'db1':Daubechies小波是离散小波变换(Discrete Wavelet Transform, DWT)中常用的小波函数。Daubechies小波是紧支撑的小波,适用于处理有限长度的信号。 'haar':Haar小波是最简单的小波函数之一,适用于对信号进行基本的低通和高通分解; 'mexh':Mexican Hat小波,也称为Ricker小波,适用于处理具有尖峰或波包特性的信号; 'bior1.1':Bior小波是一类双正交小波,其特点是具有对称和非对称两组滤波器,尤其适用于一些信号的多分辨率分析,如图像处理; 'sym2':Symlet小波(Symmetric Wavelets),是一类对称的小波函数,它在某些方面类似于Daubechies小波,但是Symlet小波在设计上更加灵活。Symlet小波也是一种紧支撑小波,适用于有限长度的信号处理。 小波函数的选择通常取决于处理的信号类型以及分析的目标。在实际应用中,可以尝试不同的小波函数,观察它们在信号上的效果,然后根据实验结果选择最适合的小波函数。在选择小波函数时,也要考虑小波函数的性质,如平滑性、局部化等。 2.3 凯斯西储大学轴承数据的加载选择正常信号和 0.021英寸内圈、滚珠、外圈故障信号数据来做对比 第一步,导入包,读取数据 import numpy as np from scipy.io import loadmat import numpy as np from scipy.signal import stft import matplotlib.pyplot as plt import matplotlib matplotlib.rc("font", family='Microsoft YaHei') # 读取MAT文件 data1 = loadmat('0_0.mat') # 正常信号 data2 = loadmat('21_1.mat') # 0.021英寸 内圈 data3 = loadmat('21_2.mat') # 0.021英寸 滚珠 data4 = loadmat('21_3.mat') # 0.021英寸 外圈 # 注意,读取出来的data是字典格式,可以通过函数type(data)查看。第二步,数据集中统一读取 驱动端加速度数据,取一个长度为1024的信号进行后续观察和实验 # DE - drive end accelerometer data 驱动端加速度数据 data_list1 = data1['X097_DE_time'].reshape(-1) data_list2 = data2['X209_DE_time'].reshape(-1) data_list3 = data3['X222_DE_time'].reshape(-1) data_list4 = data4['X234_DE_time'].reshape(-1) # 划窗取值(大多数窗口大小为1024) data_list1 = data_list1[0:1024] data_list2 = data_list2[0:1024] data_list3 = data_list3[0:1024] data_list4 = data_list4[0:1024]第三步,进行数据可视化 plt.figure(figsize=(20,10)) plt.subplot(2,2,1) plt.plot(data_list1) plt.title('正常') plt.subplot(2,2,2) plt.plot(data_list2) plt.title('内圈') plt.subplot(2,2,3) plt.plot(data_list3) plt.title('滚珠') plt.subplot(2,2,4) plt.plot(data_list4) plt.title('外圈') plt.show()
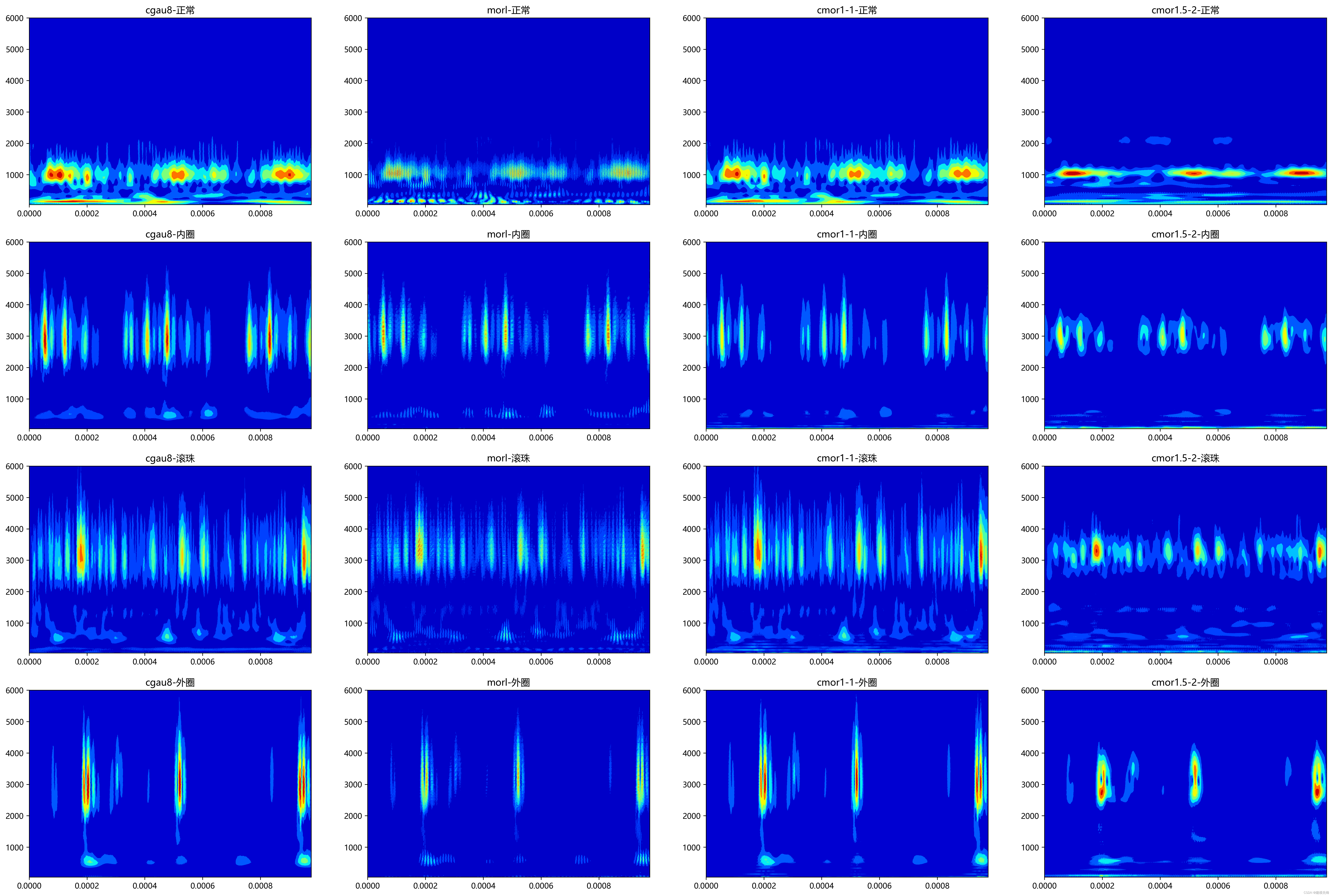
本实验以某轴承故障诊断论文推荐'cgau8'小波,以及'morl'小波、'cmor1-1'小波、'cmor1.5-2'小波为实验做对比,尺度先设定为128,来对比不同小波函数的影响。 2.4.1 基于尺度为128,选择内圈数据比较 CWT 的不同小波函数 import numpy as np import matplotlib.pyplot as plt import pywt import pandas as pd # 连续小波变换参数 # 采样频率 sampling_rate = 1024 # 尺度长度 totalscal = 128 wavename1 = 'cgau8' fc1 = pywt.central_frequency(wavename1) cparam1 = 2 * fc1 * totalscal scales1 = cparam1 / np.arange(totalscal, 0, -1) wavename2 = 'morl' # fc2 = pywt.central_frequency(wavename2) cparam2 = 2 * fc2 * totalscal scales2 = cparam2 / np.arange(totalscal, 0, -1) wavename3 = "cmor1-1" fc3 = pywt.central_frequency(wavename3) cparam3 = 2 * fc3 * totalscal scales3 = cparam3 / np.arange(totalscal, 0, -1) wavename4 = 'cmor1.5-2' fc4 = pywt.central_frequency(wavename4) cparam4 = 2 * fc4 * totalscal scales4 = cparam4 / np.arange(totalscal, 0, -1) # 进行连续小波变换 coefficients1, frequencies1 = pywt.cwt(data_list2, scales1, wavename1, sampling_period) coefficients2, frequencies2 = pywt.cwt(data_list2, scales2, wavename2, sampling_period) coefficients3, frequencies3 = pywt.cwt(data_list2, scales3, wavename3, sampling_period) coefficients4, frequencies4 = pywt.cwt(data_list2, scales4, wavename4, sampling_period) # 小波系数矩阵绝对值 amp1 = abs(coefficients1) amp2 = abs(coefficients2) amp3 = abs(coefficients3) amp4 = abs(coefficients4) # 根据采样频率 sampling_period 生成时间轴 t t = np.linspace(0, 1.0/sampling_rate, sampling_rate, endpoint=False) 数据可视化 plt.figure(figsize=(20,10)) plt.subplot(2,2,1) plt.contourf(t, frequencies1, amp1, cmap='jet') plt.title('内圈-cgau8') plt.subplot(2,2,2) plt.contourf(t, frequencies2, amp2, cmap='jet') plt.title('内圈-morl') plt.subplot(2,2,3) plt.contourf(t, frequencies3, amp3, cmap='jet') plt.title('内圈-cmor1-1') plt.subplot(2,2,4) plt.contourf(t, frequencies4, amp4, cmap='jet') plt.title('内圈-cmor1.5-2') plt.show()
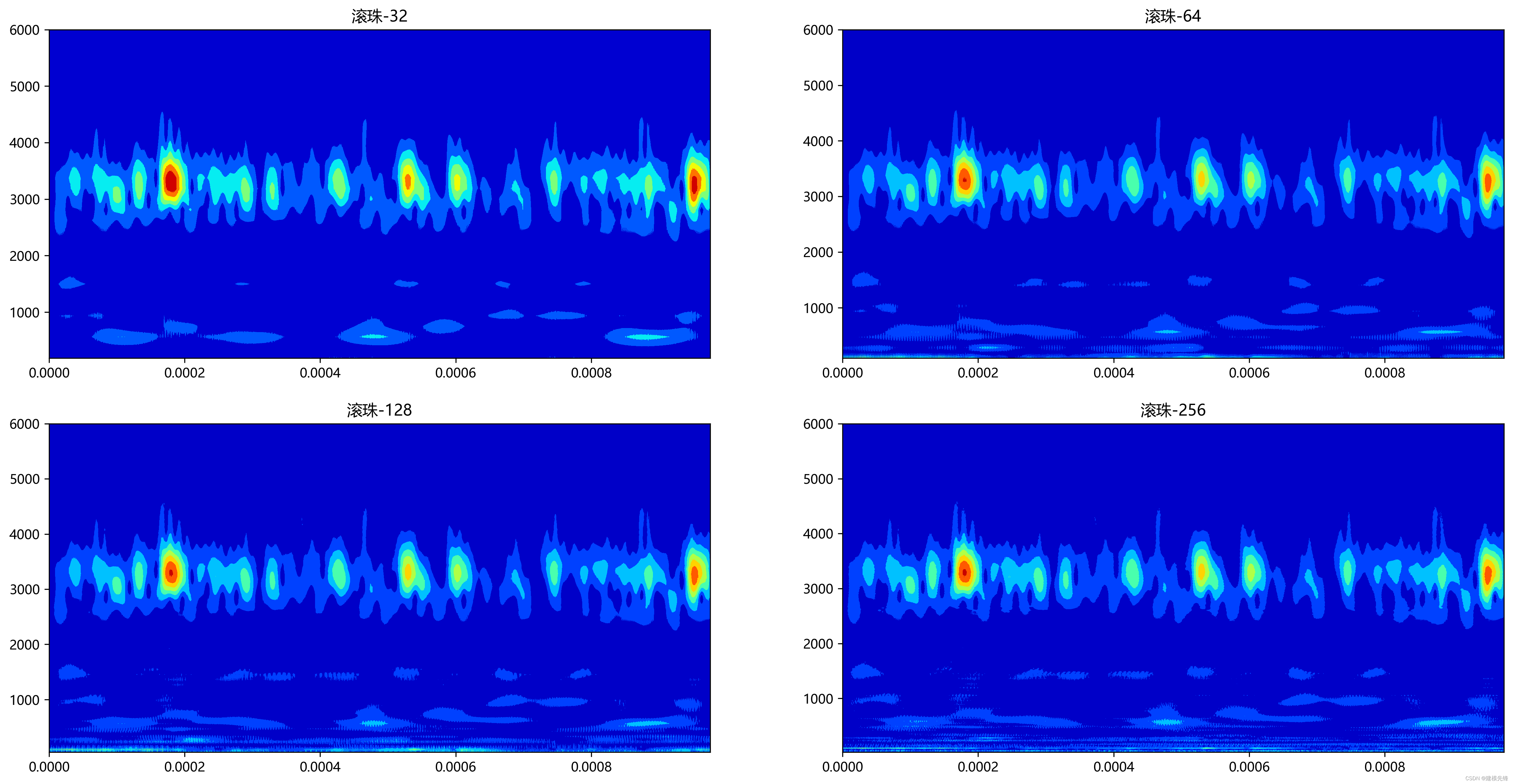
比较来看,'cgau8'小波和'cmor1.5-2'小波对于不同故障都有着较高的辨识度,综合考虑频率分辨率和时间分辨率,选择'cmor1.5-2'小波来进一步分析。 2.4.3 基于'cmor1.5-2'小波,选择滚珠故障数据比较 CWT 的不同尺度的变化:32、64、128、256;同时尺度序列scales的常数项cparams均采用:cparam = 2 * fc * totalscal;'cmor1.5-2'小波中1 代表中心频率参数,1.5代表带宽参数;
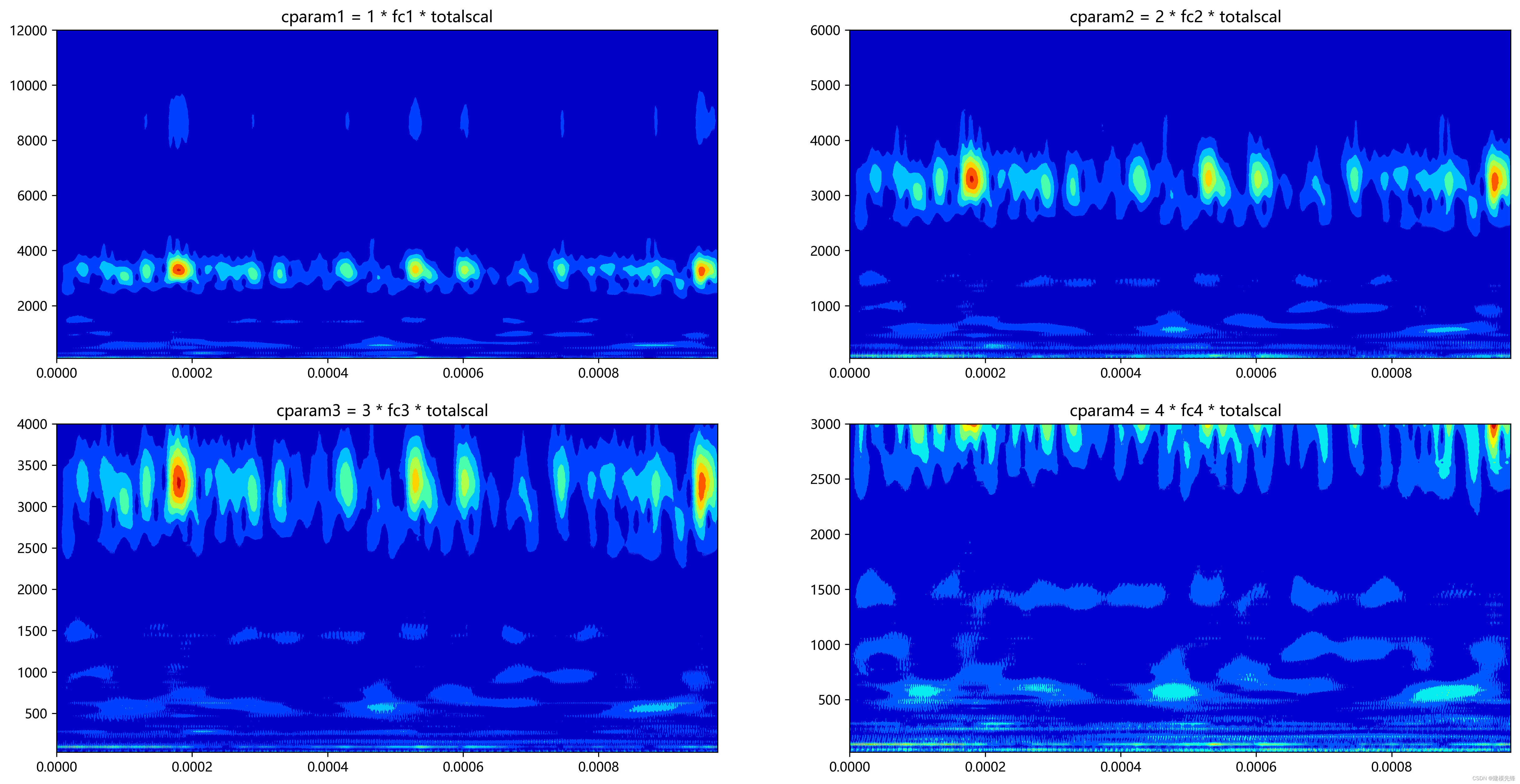
注意,在连续小波变换中,影响小波系数的是尺度序列scales,但是仍能从上图中看出尺度长度越大,对低频特征关注越多(注意每幅小图 的底部低频的区别); 为进一步探索尺度序列scales的影响,选择尺度长度为128,设置不同常数项cparams来观察对时频变换的影响: import numpy as np import matplotlib.pyplot as plt import pywt import pandas as pd # 连续小波变换参数 # 采样频率 sampling_rate = 1024 # 尺度长度 totalscal = 128 wavename1 = 'cmor1.5-2' fc1 = pywt.central_frequency(wavename1) cparam1 = 1 * fc1 * totalscal scales1 = cparam1 / np.arange(totalscal, 0, -1) wavename2 = 'cmor1.5-2' # fc2 = pywt.central_frequency(wavename2) cparam2 = 2 * fc2 * totalscal scales2 = cparam2 / np.arange(totalscal, 0, -1) wavename3 = "cmor1.5-2" fc3 = pywt.central_frequency(wavename3) cparam3 = 3 * fc3 * totalscal scales3 = cparam3 / np.arange(totalscal, 0, -1) wavename4 = 'cmor1.5-2' fc4 = pywt.central_frequency(wavename4) cparam4 = 4 * fc4 * totalscal scales4 = cparam4 / np.arange(totalscal, 0, -1) # 进行连续小波变换 coefficients1, frequencies1 = pywt.cwt(data_list3, scales1, wavename1, sampling_period) coefficients2, frequencies2 = pywt.cwt(data_list3, scales2, wavename2, sampling_period) coefficients3, frequencies3 = pywt.cwt(data_list3, scales3, wavename3, sampling_period) coefficients4, frequencies4 = pywt.cwt(data_list3, scales4, wavename4, sampling_period) # 小波系数矩阵绝对值 amp1 = abs(coefficients1) amp2 = abs(coefficients2) amp3 = abs(coefficients3) amp4 = abs(coefficients4) # 根据采样频率 sampling_period 生成时间轴 t t = np.linspace(0, 1.0/sampling_rate, sampling_rate, endpoint=False) 进行可视化 plt.figure(figsize=(20,10), dpi=300) plt.subplot(2,2,1) plt.contourf(t, frequencies1, amp1, cmap='jet') plt.title('滚珠-32') plt.subplot(2,2,2) plt.contourf(t, frequencies2, amp2, cmap='jet') plt.title('滚珠-64') plt.subplot(2,2,3) plt.contourf(t, frequencies3, amp3, cmap='jet') plt.title('滚珠-128') plt.subplot(2,2,4) plt.contourf(t, frequencies4, amp4, cmap='jet') plt.title('滚珠-256') plt.show()
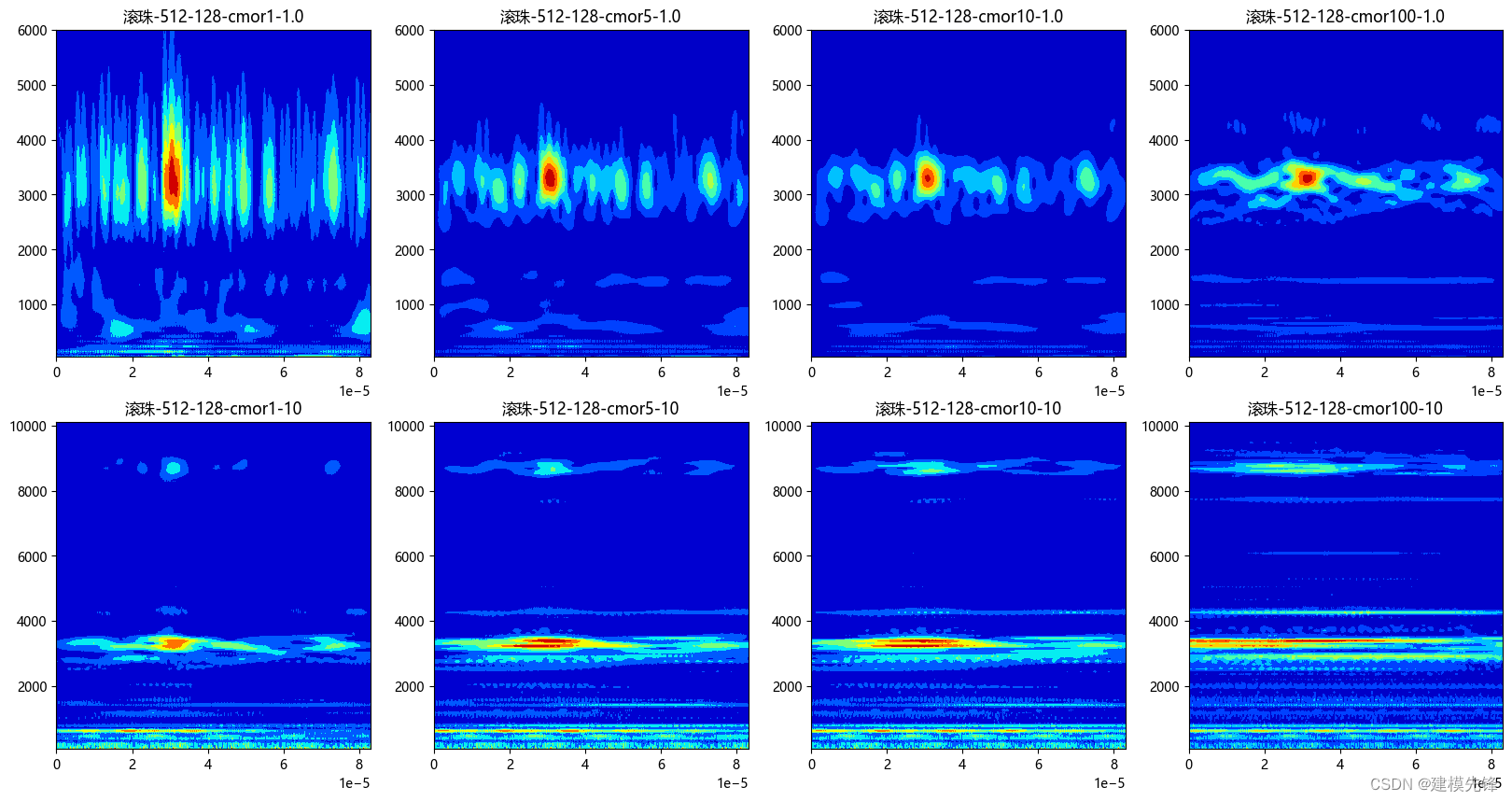
对于不同尺度序列scales的比较,更能说明之前的结论: 高频特征: 如果关注信号的高频特征,应该选择较小的尺度; 低频特征: 如果关注信号的低频特征,应该选择较大的尺度; 对于滚珠故障类型数据,从时频图结果来看,应该选择2倍的cparams参数,有着较高的频率分辨率,和我们感兴趣的频率区域。 2.4.4 比较cmor小波函数 不同参数 ----中心频率,带宽参数
在轴承故障诊断中,中心频率和带宽的具体设置取决于多个因素,包括轴承类型、工作条件和故障特征等。由于每个应用场景和故障类型都有所不同,没有一个通用的固定数值。以下是一些常见的参考范围和建议: 中心频率(Center Frequency): 对于滚动轴承,常见的故障频率范围在几百赫兹到几千赫兹之间。可以选择在这个范围内的适当值作为中心频率。 根据具体的故障类型,例如滚动体故障、内圈故障或外圈故障,可能需要设置不同的中心频率。 带宽(Bandwidth): 带宽的选择取决于信号的特征和所需的时频分辨率。 通常情况下,较小的带宽值(如1-5)适用于较短时域特征,能够提供更好的时频局部化能力。 如果需要更好的频率分辨率,可以选择较大的带宽值(如10-20),但可能会牺牲一部分时频局部化能力。 这些值仅供参考,实际应用时需要进行实验和调整,根据信号的频谱特征和故障频率范围来确定最佳的参数配置。建议通过观察生成的时频图,确保故障频率和特征得到适当的捕捉和展示。同时,根据实际的故障案例和经验,不断调整参数以提高故障诊断的准确性和可靠性。 经过大量的对比实验和观察,本文得出最后的参数结论设置: # 尺度长度 totalscal = 128 # 小波基函数 wavename = 'cmor100-1' # 小波函数中心频率 fc = pywt.central_frequency(wavename) # 常数c cparam = 2 * fc * totalscal # 小波尺度序列 scales = cparam / np.arange(totalscal, 0, -1)来实现对故障数据的诊断分类。 3 基于时频图像的轴承故障诊断分类下面以连续小波变换(CWT)作为轴承故障数据的处理方法进行讲解: 数据介绍,凯斯西储大学(CWRU)轴承数据10分类数据集
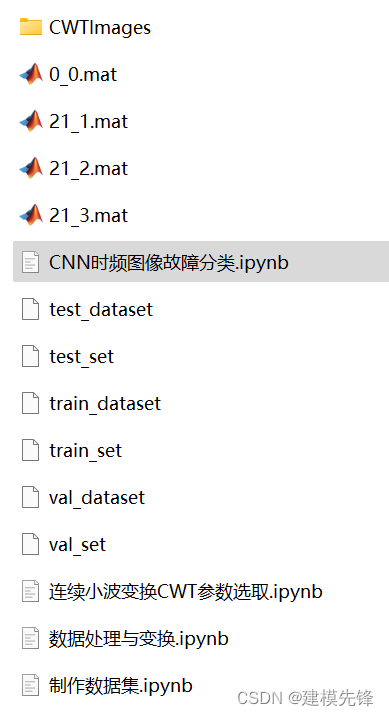
train_set、val_set、test_set 均为按照7:2:1划分训练集、验证集、测试集,最后保存数据 3.1 生成时频图像数据集
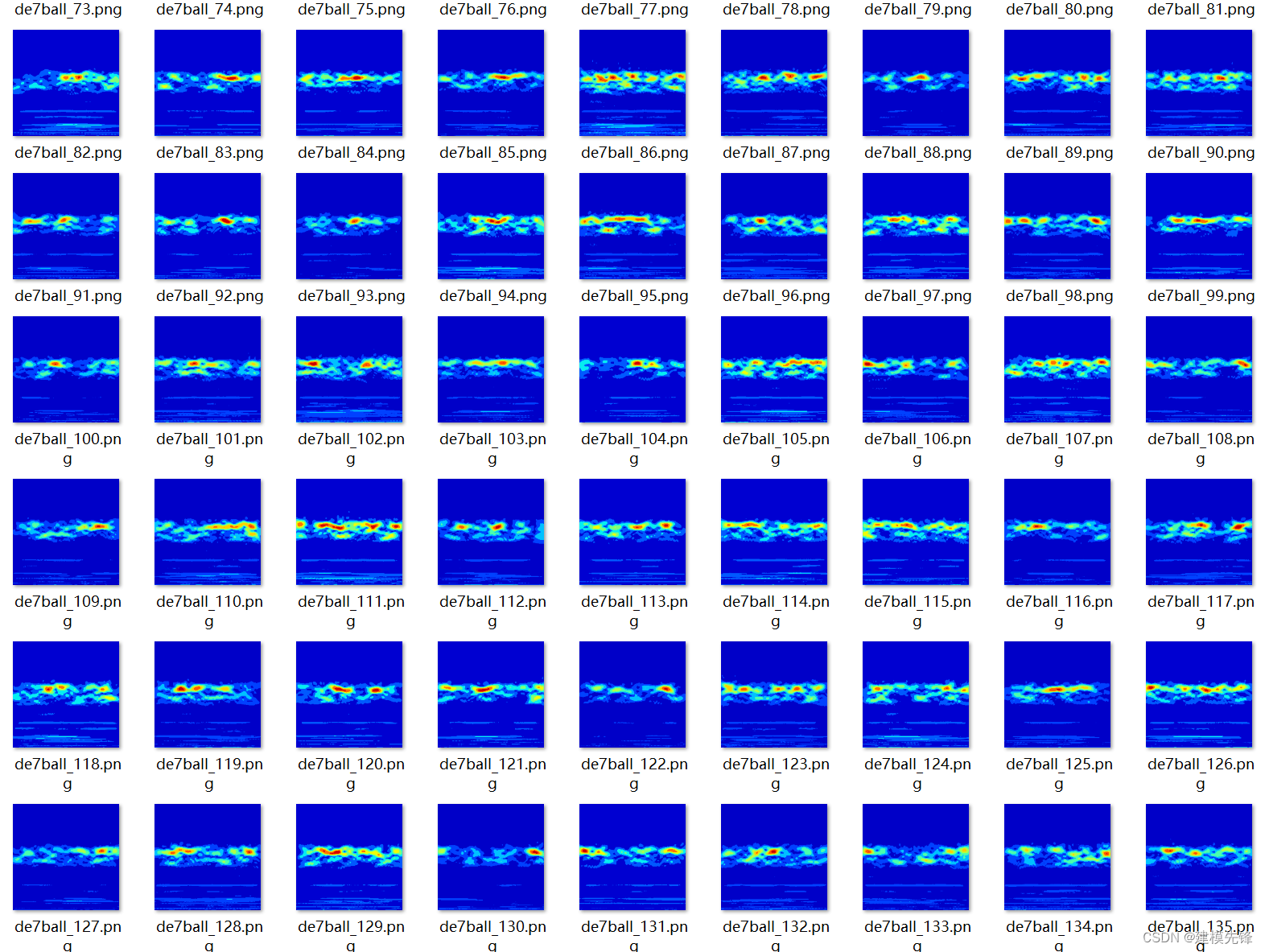
如图所示为生成的时频图像数据集
制作数据标签,保存数据
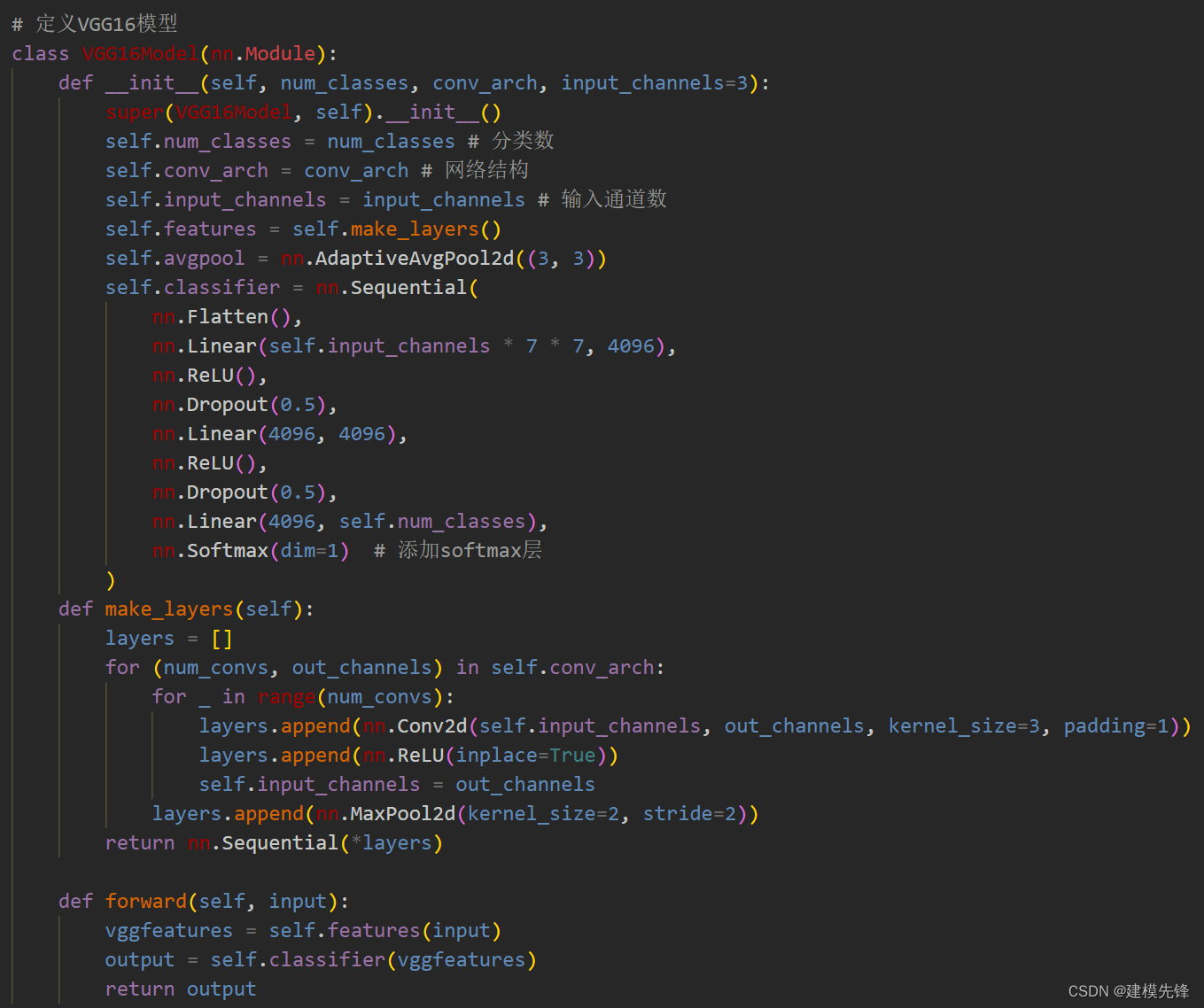
定义VGG网络模型
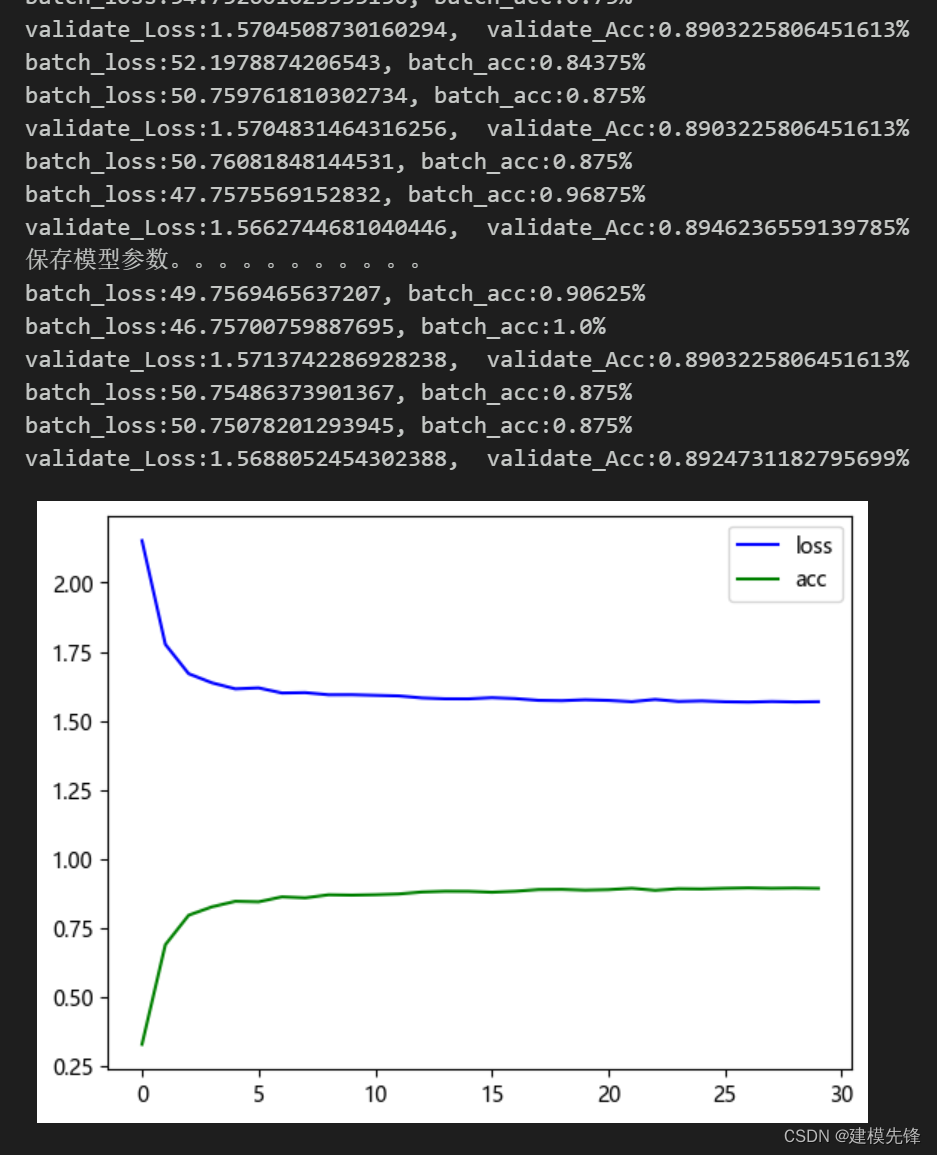
3.3 设置参数,训练模型
30个epoch,准确率将近90%,继续调参可以进一步提高分类准确率 参考文献 [1]《小波分析及其工程应用》.机械工业出版社
|
【本文地址】
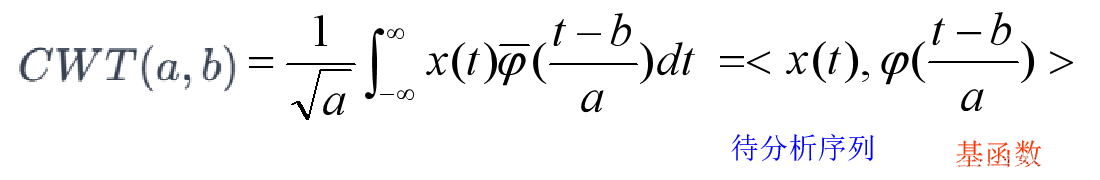


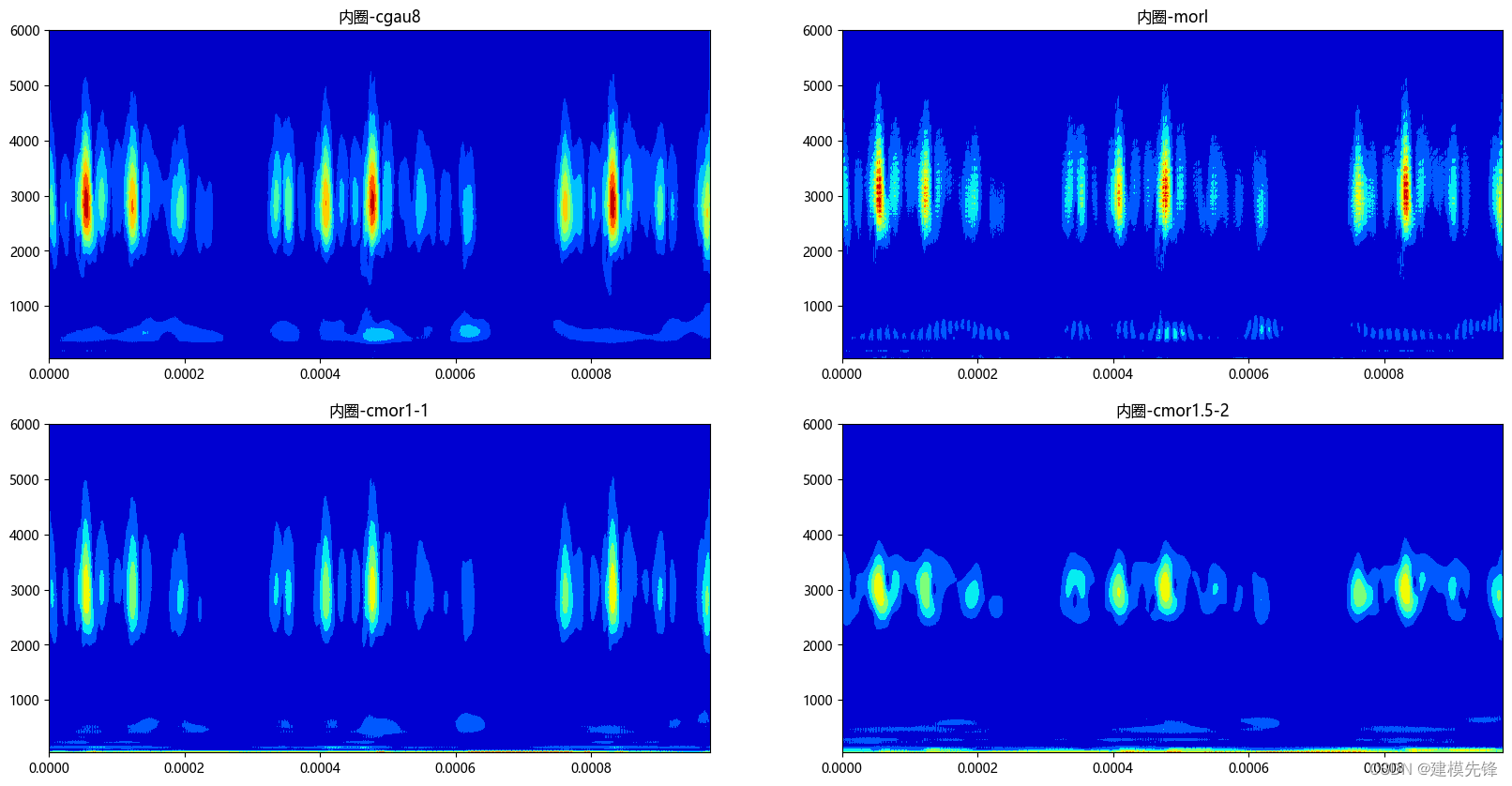 对比不同小波函数,对于内圈故障信号来说,'cgau8'小波有着较高的频率分辨率,需要对比其他类型故障数据,进一步观察。
对比不同小波函数,对于内圈故障信号来说,'cgau8'小波有着较高的频率分辨率,需要对比其他类型故障数据,进一步观察。