A. Jacot, F. Gabriel, and C. Hongler, ‘Neural Tangent Kernel: Convergence and Generalization in Neural Networks’. arXiv, Feb. 10, 2020. Accessed: Mar. 18, 2023. [Online]. Available: http://arxiv.org/abs/1806.07572

当然，这篇随笔并不只是上面这篇开山之作（NIPS 2018）的阅读笔记，而是融合了我所需要的NTK相关的基本知识。

某种意义上写这篇博客有点“不务正业”了，因为和目前想做的内容没有直接相关。之所以决定好好记录一下NTK是因为最近看到的几篇理论文章在推导时都应用了NTK的假设和一部分内容，并且认真了解网络动力学和优化相关的理论更利于随后工作的开展。反正学到就是赚到（打好数理基础肯定不吃亏？）

神经网络在提出初期存在许多质疑，包括但不限于如下内容

Non-convexity

神经网络不是凸函数，会存在许多局部极小值，梯度下降最终得到的结果与真正的极小值点是否有较大差别？

Initialization

从不同初始化下进行梯度下降，最终结果是否会有较大偏差呢？

Interpretability

神经网络如何被描述？众多神经元和参数有哪些内在联系？

Generalization

神经网络参数很多，理论上很容易过拟合，但是在测试集上的表现还不错，表现出较好的泛化性能，如何解释呢？

譬如，对第四点，机器学习的传统观点认为，在训练误差和泛化差距之间要进行谨慎的权衡。模型的复杂性存在一个“最佳点”。因此如果模型足够大，就可以实现合理良好的训练误差；而模型足够小，才可以降低泛化差距（测试误差和训练误差之间的差）。较小的模型会产生较大的训练误差，而使模型变大则会导致较大的泛化差距，两者都会导致较大的测试误差。测试误差随模型复杂度的变化可以经典U形曲线来描述（如下图a，图片来自文献Reconciling modern machine learning practice and the bias-variance trade-off）

但是，如今很常见的是使用高度复杂的过参数化模型，例如深度神经网络。通常对这些模型进行训练，以在训练数据上实现接近零的误差，但是它们仍然在测试数据上具有出色的性能。上图的作者Belkin等人通过“双重下降”曲线对这一现象进行了描述，该曲线扩展了经典的U形曲线（如上图b），并对此进行了理论解释。可以观察到，随着模型复杂度增加到可以完全拟合训练数据的程度（即达到插值制度），测试误差继续下降！有趣的是，最好的测试效果通常是通过最大的模型实现的，这与关于“最佳点”的经典直觉背道而驰。

因此，有人怀疑深度学习中使用的训练算法（（随机）梯度下降及其变体）以某种方式隐含地限制了训练网络的复杂性（即参数的“真实数量”），从而导致了较小的概括差距。

更直接点，举个例子，比如单目标分类，有时候数据还没有网络参数多，相当于一个有很多未知量的式子，但是限制它的方程数量却很少，那么这样一个自由度很高但约束很少的式子，怎么能符合我们对其专一且严格的要求呢？

NTK是一种较成功的解释以上质疑的技术性理论，它有两个假设：

第二条假设某种意义上对应人们之前对深度神经网络泛化性能和参数量的怀疑，而第一条假设是一个先决条件，即，在我们训练过程中，网络中不应该出现梯度的爆炸或者消失，而是保持均匀

并且，顾名思义，神经正切核Neural Tangent Kernel是一种核方法，1994年Priors for Infinite Networks就已经提出了无限宽的神经网络和核方法之间的联系。近几年内，NTK相关的基础理论文章得到了几个惊人的结论，比如

这些结论很好地解释了很多对于神经网络优化的质疑。接下来我们会依次介绍对应的条件（或者假设）下的推导和近似

正如其名字，这个初始化方法是大佬何恺明ICCV 2015的工作, Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification 提出的

初始化的意义在于调整各层神经元的方差，确保不会出现梯度爆炸和梯度消失的情况。从自然科学的角度来看，可以说这样初始化调整后的网络具有某种意义上的空间平移不变性，我们希望这种“空间对称性”可以为神经网络带来一个类似“动量守恒”一样的守恒量

在何恺明之前的Xavier初始化对激活函数对称性要求较高，没有很好地考虑到激活函数为非奇函数时 \(E(\sigma(x))\neq 0\) 的情况（考虑对了量级，但是没有根据激活函数的性质调整参数），所以并不很适用于RELU这种激活函数，而何恺明考虑到了这种情况，Kaiming Initialization可以应用于非奇函数。

许多文献的符号约定都不尽相同，这里我自己定一套吧

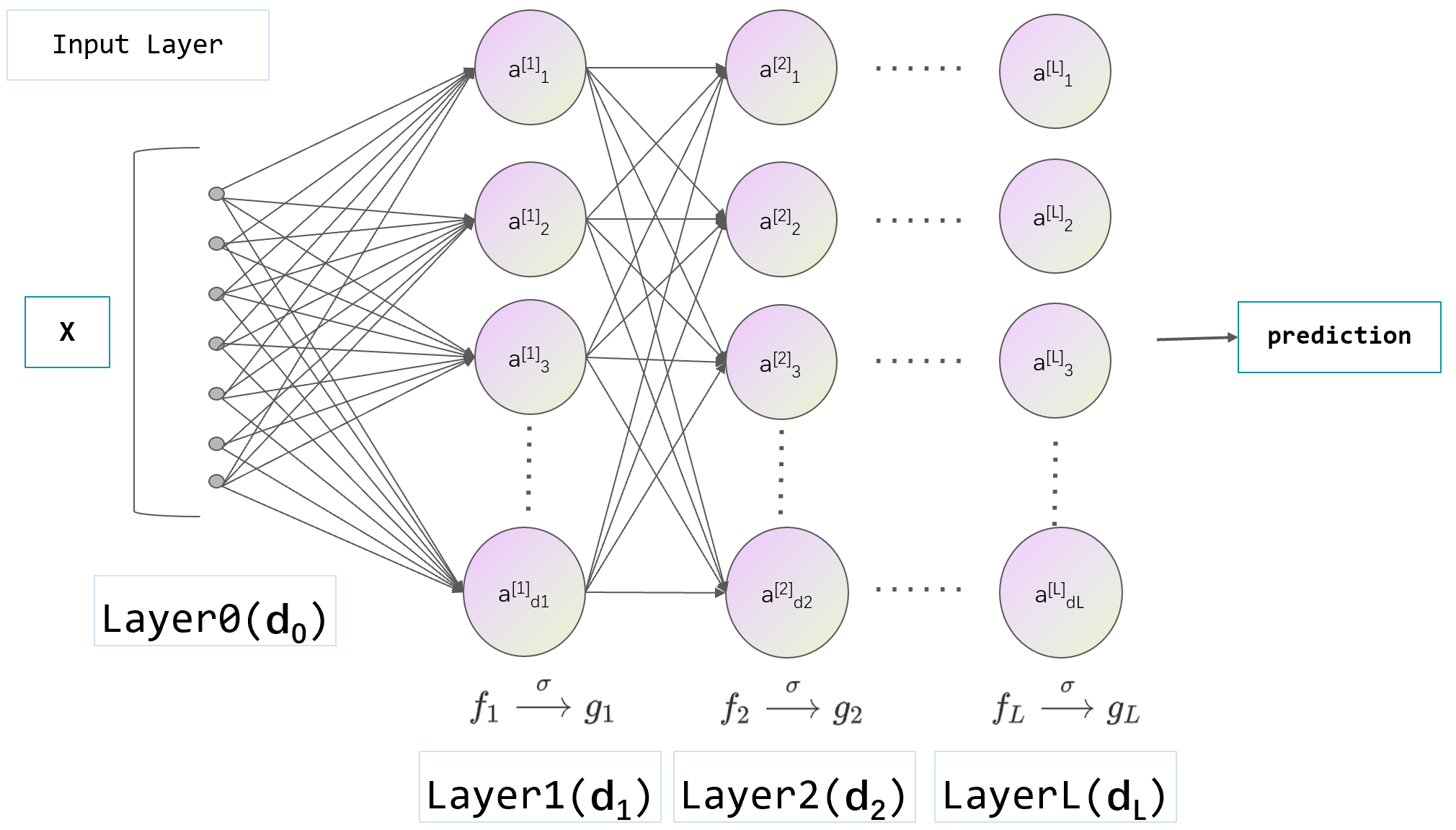
如上图（好难画），定义一个有 L 层的ANN：

即，将维度为P的参数 \(\theta\) 映射到一个属于函数域 \(\mathcal F\) 的函数 \(f(\boldsymbol x , \theta)\) ，有 \(f(\boldsymbol x , \theta): \mathcal{X} \rightarrow \mathcal{Y}\) 。

其中 \(f(\boldsymbol x , \theta)\) 即参数为 \(\theta\) 的ANN。这里 \(P=\sum_{l=1}^{L}(d_{l-1}+1)(d_l)\) （已将偏置考虑为一个特殊神经元），其中 \(l-1\) 层与 \(l\) 层之间的连接矩阵 \(\boldsymbol\omega_l\) 的参数量为 \((d_{l-1}+1)(d_l)\) 。

第 \(l\) 层的神经元数量为 \(d_l\) ，输入向量 \(\boldsymbol x\in\mathbb{R}^{d}\) ，将 \(\boldsymbol x\) 看作第\(0\)层神经元，则有 \(d=d_0\)

我们定义第h层神经元的值为向量 \(f_l(\boldsymbol x)\) ，在经过激活函数 \(\sigma\) 后的值为 \(g_l(\boldsymbol x)\) ，不难写出前向传播时的递推公式：

因为将 \(\boldsymbol x\) 看作第\(0\)层神经元，所以有 \(g_0(\boldsymbol x)=\boldsymbol x\)

很好理解的一点是，既然我们的网络参数都已经奔着标准正态分布初始化了，那么聪明的读者当然会想到，输入的 \(\boldsymbol x\) 肯定已经被初始化为一个符合标准正态分布的 \(d\) 维矢量（这很好做到，并且大伙都已经这么干了）

为了得到守恒量，我们需要改写神经网络，给参数 \(\boldsymbol\omega_l\) 乘一个常数 \(\sqrt{\frac{C_\sigma}{d_l}}\) ，那么原前向传播递推式可以写为：

我们称其为网络的标准形式。

其中 \(C_\sigma\) 是与激活函数 \(\sigma\) 相关的一个常数， \(C_\sigma=\frac1{E_{z\sim N(0,1)}{(\sigma(z))}^{2}}\) ，之所以这样做，是为了保持 \(f_l(\boldsymbol x)\) 的元素（就是神经元进激活函数 \(\sigma\) 前的数值）在前向传播中不受每层神经元数量变化影响，保持标准差大约为1，这样可以允许我们堆叠更多层而不会出现梯度爆炸或消失。

为方便理解 \(C_\sigma\) ，打个比方，对于 \(\sigma(z)=\mathsf{LELU}(z)=z^+\) ，那么 \(C_\sigma\) 就是标准正态分布方差的一半（\(\frac12\)）分之一，也就是2，这样在一半左右的神经元被置\(0\)的情况下，整体标准差还是1。这里的 \(C_\sigma=[E_{z\sim N(0,1)}{(\sigma(z))}^{2}]^{-1}\) 其实已经包含了一个重要的假设——那就是认为神经元的数值分布符合 \(z\sim N(0,1)\) ，这就涉及到我们的重要假设——特殊的参数初始化，Kaiming Initialization

与我们“标准形式”网络假设对应的，我们需要初始化参数 \(\boldsymbol\omega_l\sim N(0,1)\)

我们将参数 \(\sqrt{\frac{C_\sigma}{d_l}}\) 写进 \(\sigma\) 后，不妨令 \(\tilde{\boldsymbol\omega}_l=\sqrt{\frac{C_\sigma}{d_l}}\boldsymbol\omega_l\) ，可以得到更方便的标准形式前向传播表达式：

这样我们的参数初始化可以写为

这就是大佬论文原文使用的初始化方法

推导不算难，就是手敲公式略麻烦

第 \(l\) 层的方差 \(\operatorname{Var}\left(f_l(\boldsymbol x)\right)\) 为：

我们的参数初始化应该使得 \(E(\boldsymbol\omega_l)=0\) ，所以只剩下第一项

这里我们认为更具有普适性的 \(E(\sigma(x))\neq 0\) （譬如激活函数为非奇函数RELU），则方差可以写为

这里我们不妨用一点数学归纳法的思想，已知 \(f_{0}(\boldsymbol x)=\boldsymbol x\sim N(0,1)\) ，我们希望上一层的神经元在进激活函数前满足 \(f_{l-1}(\boldsymbol x)\sim N(0,1)\) ，所以我们假设 \(f_{l-1}(\boldsymbol x)\sim N(0,1)\) ，看看这一层需要什么样的要求才能让本层神经元也满足 \(f_{l}(\boldsymbol x)\sim N(0,1)\) 。将前向传播式带入 \(E\left(g_{l-1}(\boldsymbol x)\right)^{2}\) 中，用 \(f_{l-1}(\boldsymbol x)\) 表示，不难得到

根据我们之前的假设， \(\boldsymbol\omega_l\sim N(0,1)\) ，所以 \(\operatorname{Var}\left(\boldsymbol\omega_l\right)=1\) ，因此 \(l\) 层神经元方差为

所以我们只需要在式子中乘一个 \(\frac{C_\sigma}{d_l}\) 就可以了，最方便的方式就是在 \(\boldsymbol\omega_l\) 前面补个常系数 \(\sqrt{\frac{C_\sigma}{d_l}}\) ，也就是之前所说的 \(\tilde{\boldsymbol\omega}_l=\sqrt{\frac{C_\sigma}{d_l}}\boldsymbol\omega_l\) ， \(\tilde{\boldsymbol\omega}_l\sim N(0,{\frac{C_\sigma}{d_l}})\) ，进行这样的修正之后，就可以得到前向传播中方差不变（理论上）的标准网络形式了

这里其实有个逻辑漏洞没有补上，就是我们证明了这种参数修正下满足传入 \(f_{l-1}(\boldsymbol x)\sim N(0,1)\) 可以得到均值为\(0\)，方差为1的 \(f_l(\boldsymbol x)\) ，但是并不能说明 \(f_l(\boldsymbol x)\) 时正态分布，因为无限宽网络神经元的参数传递满足独立同分布在当时还没有证明（并不是如我们所想地那样显而易见）。后续谷歌的人2018年用Deep Neural Networks as Gaussian Processes补上了这个漏洞，不过因为篇幅和时间有限，这里当作一个小引理使用了。

举个具体的例子，对于RELU，则有：

这就不难解释对于对于 \(\sigma(z)=\mathsf{LELU}(z)=z^+\) 时，为什么 \(C_\sigma\) 等于2了——就是为了消掉分母中的2（先放在开根号中再随方差运算平方后还是本身）

如果只是对梯度量级的估计，那么在全部标准正态分布初始化的基础上只要修正的参数能 \(\sim \frac 1{\sqrt{d_l}}\) 就可以，甚至无所谓在激活函数内还是外

这里我们研究学习率 \(\eta\) （梯度下降步长）趋于无穷小时网络表现出的行为

考虑神经网络 \(f(\boldsymbol x , \theta): \mathcal{X} \rightarrow \mathcal{Y}\) 以拟合目标函数 \(f^*(\boldsymbol x)\) ，

定义数据集 \({\{(\boldsymbol x_i,\boldsymbol y_i)\}}_{i=1}^n\) 和采样函数：

其中 \(\delta(\boldsymbol x)\) 就是冲击采样函数。不难发现 \(\rho(\boldsymbol x)\) 作为概率密度函数在 \(\mathbb{R}^{d}\) 上连续，这样我们就可以得到连续形式下的损失函数，以均方根误差（MSE）为例：

使用梯度下降进行训练

就不具体阐述梯度下降的物理意义了，注意这里的t代表的是一个时间尺度的概念，但并不具有时间量纲，所以可以人为设定 \(t^{+}=t+\eta\) ，令 \(\eta\rightarrow 0\) ，则可以得到 \(\boldsymbol\theta(t)\) 随训练步数在学习率趋于\(0\)下的连续演变近似形式：

可以看出 \(\theta\) 随训练步数的演变，其实就是损失函数关于 \(\theta\) 的负梯度，也就是 梯度流的形式

可以发现 \(\eta\rightarrow 0\) 条件下损失L随着训练步数增加时非递增的（不言而喻）

我们定义神经网络的输出 \(f(\boldsymbol{x},\boldsymbol{\theta})\) 和目标函数 \(f^*(\boldsymbol{x})\) 之间的偏差 \(u(t, \boldsymbol{x}) =f(\boldsymbol{x}, \boldsymbol{\theta})-f^*(\boldsymbol{x})\)

我们可以得到描述误差随训练步数变化的方程，也就是网络训练的动力学方程：

这里我们令 \(u_{\rho}\left(\boldsymbol{x}^{\prime}\right)=\frac{\partial \mathbf{Loss}}{\partial f\left(\boldsymbol{x}^{\prime}, \boldsymbol{\theta}\right)}\rho\left(\boldsymbol{x}^{\prime}\right)\) ，其中 \(\mathbf{Loss}\) 是对于具体样例来说的损失函数，比如对于MSE， \(\mathbf{Loss}=\frac12{[f(\boldsymbol{x}, \boldsymbol{\theta})-f^*(\boldsymbol{x})]}^2\)

从上式不难看出误差随时间的演变过程可以被线性描述为与时间无关的核。定义核函数

为了更直观理解这个核函数，可以将其写为：

可以将其理解为网络在训练过程中，输入一个位于 \(x\) 的数据点对监督样例 \((x',f^* (x'))\) 优化的灵敏度，表现为网络最终输出的变化

那么可以将动力学方程表示为：

我们希望用离散的方式来描述上面的动力学方程，因为 \(\boldsymbol{x}^{\prime}\) 是任取的，所以我们对于训练集 \({\{(\boldsymbol x_i,\boldsymbol y_i)\}}_{i=1}^n\) 中的每一组数据，定义

特别地，当loss函数取MSE时， \(u_L(\mathcal X)=u(\mathcal X)\) ，整个网络形式更加简单

千万注意， \(K\) 和 \(u_\rho(\mathcal X)\) 都不是常数， \(K,u_\rho(\mathcal X)\sim\theta\sim t\) ，与网络参数有关，所以也与时间相关

将这个网络的动力学方程向量化表示为

这是一个非线性一阶常微分方程。由上式可以看出， \(K(\boldsymbol x,\mathcal X)\) 是由网络参数结构决定的， \(u(\mathcal X)\) 由数据集决定，当 \(u(\mathcal X)=0\) ，演化过程训练停止

更进一步，考虑任取样例 \(\boldsymbol x\) 的情况，离散形式动力学方程可以写作：

其中 \(K(\mathcal X,\mathcal X)\in\mathbb{R}^{n*n}\) 被称作Gram Matrix，有

小推论：Gram Matrix \(K\) 的正定性证明：

令 \(\phi(\mathcal X)=[\nabla_{\boldsymbol{\theta}} f\left(\boldsymbol x_{i_1}, \boldsymbol{\theta}\right)],\cdots,\nabla_{\boldsymbol{\theta}} f\left(\boldsymbol x_{i_n}, \boldsymbol{\theta}\right)\) ，则 \(K=\phi(\mathcal X)\cdot\phi^T(\mathcal X)\)

对 \(\forall\,{V}\in \mathbb{R}^{n}\) ，

因此 \(K\in S_+^n\)

为了得到一个不与时间有关的守恒量，我们引入一个重要假设——神经网络隐藏层无限宽 ，也就是 \({d_l}\rightarrow +\infty,l\neq0\) ，因此 \(\theta\) 的参数量 \(P=\sum_{l=1}^{L}(d_{l-1}+1)(d_l)\rightarrow+\infty\) ，那么由强大数定律可以发现， \(K\) 会趋近于一个常数矩阵 \(G\) ，也就是说与时间无关：

据此，我们就得到了更为方便的无限宽近似下的网络动力学方程

或者其连续形式

下面说明，在隐藏层无限宽下，NTK就是一个不随时间变化的常数矩阵：在Kaiming Initialization（或者相同量级的初始化）条件下，参数 \(\boldsymbol\omega\sim N(0,\frac{C_\sigma}d)\) ，在宽度d很大时，参数被限制在很小的域内，变化量也趋于\(0\)，因此我们可以用一阶泰勒展开来估计网络最终的状态

后文中简记，用 \(f(\boldsymbol{x}, {t})\) 来代表 \(f(\boldsymbol{x}, \boldsymbol{\theta}({t}))\) ，上式左右两边对 \(\theta\) 求梯度，右边常数项被干掉，一次项只剩线性系数，得

我们得到了，在网络趋近于无穷宽的一阶近似下，右边一个时间相关的项和左边的常数项相等

所以在无限宽的神经网络中，G 是会无限逼近零时刻的 G 矩阵的，也就是说

不难看出，当网络趋于无穷宽时，神经正切核 \(G\) 是一个常数矩阵，不随时间变化，误差的演化过程可以被一个简单的一阶常微分方程控制。

这意味着一个时变核变成了一个固定核。于是在这种情况下，神经网络的训练过程就变成了一个核回归的过程。

特殊地，当损失函数为MSE时， \(u_L(\mathcal X)=u(\mathcal X)\) ， \(u_{\rho}\left(\boldsymbol{x}^{\prime}\right)=u(\mathcal X){\rho}\left(\boldsymbol{x}^{\prime}\right)\)

实际经验不难发现 \(G\) 往往是一个非奇异矩阵，因此我们假定 \(G\) 最小特征值大于\(0\)

我们希望证明，因为核 \(K\) 和 \(G\) 都是正定的，只要LOSS函数是有界凸函数，那么当 \(t\rightarrow\infty\) 时，网络参数就可以收敛到最优（也就是说误差可以衰减到0）

对 \(G\) 做特征值展开

其中 \(\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_n,\,{v}_{i} \in \mathbb R^{n},\, v_{i}^{T} v_{i}=1,\, v_{i}^{T} v_{j}=0,\, i \neq j\) ，那么误差就可以被表示为

带入离散形式的动力学方程

由特征向量的正交性，对应项前系数相等

因此只要所有特征值都非负，那么这个线性常微分方程组指数收敛

我们如何直接使用我们基于无限宽假设的理论来分析实际有限宽的网络呢？换言之，对于较宽的真实网络 \(f_{nn}\) 其与无限宽下的线性化网络 \(f_{ntk}\) 的差距有多大？其实不难想到，我们当时做出无限宽假设是为了使用大数定理，因此，只要参数涨落不明显，就不会影响最终的分析结果。

严格的数学层面分析可以参照下述定理

Theorem 1 Suppose \(\sigma(z)=\max (0, z)(z \in R), 1 / \kappa=\operatorname{poly}(1 / \epsilon, \log (n / \delta)) \,d_{1}=d_{2}=\cdots= d_{L}=m\) with \(m \geq poly \left(1 / \kappa, L, 1 / \lambda_{0}, n, \log (1 / \delta)\right)\). Then for any \(\boldsymbol{x}_{t e} \in R^{d}\left\|\boldsymbol{x}_{t e}\right\|=1\), with probability at least \(1-\delta\) over the random initialization, we have

这说明，只有实际网络足够宽，实际网络与理论网络的差距很大概率可以无限小

我省略掉一些与基础理论无关的我暂时不感兴趣的内容，因为目前总结的内容基本足够我将NTK作为工具阅读分析一些理论文章

理解超参数化深度神经网络的性能绝对是一个具有挑战性的理论问题。现在，至少我们对一类超宽神经网络有了更好的理解。

我们发现，无限宽的ANN初始化等价于高斯过程，所以可以和Kernel method联系起来。然后我们证明了，训练过程也可以用一个kernel method来描述，并且能够通过kernel gradient descent来训练，这个kernel就是NTK，证明NTK在无穷宽条件下变成了一个固定核，最后证明了绝大多数情况下训练过程的收敛性，以及讨论了有限宽网络如何逼近无限宽网络的。

顺带一提，挖个大坑，无限宽隐藏层（因此符合我们希望的统计学规律），独立同分布的参数假设同样符合平均场理论，但篇幅有限，不在此探究其原理，以及两者关联。等有机会的话看看有没有时间了解一下吧（不过短时间内应该没时间填坑了）

J. Lee et al., ‘Wide Neural Networks of Any Depth Evolve as Linear Models Under Gradient Descent’, J. Stat. Mech., vol. 2020, no. 12, p. 124002, Dec. 2020, doi: 10.1088/1742-5468/abc62b.

M. Belkin, D. Hsu, S. Ma, and S. Mandal, ‘Reconciling modern machine learning practice and the bias-variance trade-off’, Proc. Natl. Acad. Sci. U.S.A., vol. 116, no. 32, pp. 15849–15854, Aug. 2019, doi: 10.1073/pnas.1903070116.

S. S. Du, J. D. Lee, H. Li, L. Wang, and X. Zhai, ‘Gradient Descent Finds Global Minima of Deep Neural Networks’. arXiv, May 28, 2019. Available: http://arxiv.org/abs/1811.03804

S. Arora, S. S. Du, W. Hu, Z. Li, R. Salakhutdinov, and R. Wang, ‘On Exact Computation with an Infinitely Wide Neural Net’. arXiv, Nov. 04, 2019. [Online]. Available: http://arxiv.org/abs/1904.11955

K. He, X. Zhang, S. Ren, and J. Sun, ‘Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification’. arXiv, Feb. 06, 2015. [Online]. Available: http://arxiv.org/abs/1502.01852

K. He, X. Zhang, S. Ren, and J. Sun, ‘Deep Residual Learning for Image Recognition’, arXiv:1512.03385 [cs], Dec. 2015, [Online]. Available: http://arxiv.org/abs/1512.03385

J. Lee, Y. Bahri, R. Novak, S. S. Schoenholz, J. Pennington, and J. Sohl-Dickstein, ‘Deep Neural Networks as Gaussian Processes’. arXiv, Mar. 02, 2018. [Online]. Available: http://arxiv.org/abs/1711.00165

G. Yang, ‘Scaling Limits of Wide Neural Networks with Weight Sharing: Gaussian Process Behavior, Gradient Independence, and Neural Tangent Kernel Derivation’. arXiv, Apr. 04, 2020. [Online]. Available: http://arxiv.org/abs/1902.04760

Some Intuition on the Neural Tangent Kernel (inference.vc)

Understanding the Neural Tangent Kernel – Rajat's Blog – A blog about machine learning and math. (rajatvd.github.io)

Ultra-Wide Deep Nets and the Neural Tangent Kernel (NTK) – Machine Learning Blog | ML@CMU | Carnegie Mellon University

机器学习12： 无穷宽神经网络之DNN in NTK regime 哔哩哔哩

深度学习理论之Neural Tangent Kernel第四讲：当NTK遇上平均场理论 - 知乎

【深度学习4】神经网络的正切核理论：引言和定义（下）哔哩哔哩