保凸运算：简单来说，保凸运算是指原来的集合 C C C是一个凸集，然后让这个凸集 C C C经过一些变换让其仍然为凸集，也即利用凸集构造凸集。保凸运算包括以下三个方面

①：交集是保凸的

②：仿射变换是保凸的，包括

③：透视变换是保凸的

④：分式线性变换是保凸的

仿射变换的保凸性：假设 f : R n → R m f:\R^{n}\rightarrow\R^{m} f:Rn→Rm是仿射变换（ x ∈ R n x\in\R^{n} x∈Rn、 f ( x ) ∈ R m f(x)\in\R^{m} f(x)∈Rm），即 f ( x ) = A x + b f(x)=Ax+b f(x)=Ax+b（也即仿射变换是线性函数和常量的组合，其中 A ∈ R m × n A\in \R^{m×n} A∈Rm×n、 b ∈ R m b\in\R^{m} b∈Rm、 A x ∈ R m × 1 Ax\in\R^{m×1} Ax∈Rm×1），则

例题： 设 x 1 , x 2 ∈ S x_{1}, x_{2}\in S x1​,x2​∈S（ S S S为凸集）， θ ∈ [ 0 , 1 ] \theta\in [0,1] θ∈[0,1]，则有凸组合 θ x 1 + ( 1 − θ ) x 2 ∈ S \theta x_{1}+(1-\theta)x_{2} \in S θx1​+(1−θ)x2​∈S；现证明经仿射变换 f f f下所形成的集合 f ( x ) f(x) f(x)为凸集

仿射变换也可通过下面的例子理解

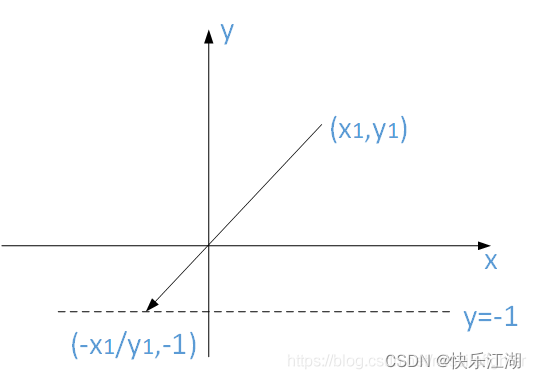
缩放和移位是保凸的：如果 S ⊆ R n S \subseteq R^{n} S⊆Rn是凸集， α ∈ R \alpha \in R α∈R， a ∈ R a \in R a∈R，那么缩放和移位后的 α S \alpha S αS和 S + a S+a S+a也是凸集

两个凸集的和是凸的：两个集合的和被定义为

S 1 + S 2 = { x + y ∣ x ∈ S 1 , y ∈ S 2 } S_{1}+S_{2}=\{x+y | x\in S_{1}, y\in S_{2}\} S1​+S2​={x+y∣x∈S1​,y∈S2​}

如果 S 1 S_{1} S1​和 S 2 S_{2} S2​是凸集，那么 S 1 + S 2 S_{1}+S_{2} S1​+S2​也为凸集

两个凸集的直积（笛卡尔积）是凸的：直积（笛卡尔积）被定义为

S 1 × S 2 = { ( x 1 , x 2 ) ∣ x 1 ∈ S 1 , x 2 ∈ S 2 } S_{1} ×S_{2}=\{(x_{1}, x_{2})|x_{1}\in S_{1}, x_{2}\in S_{2}\} S1​×S2​={(x1​,x2​)∣x1​∈S1​,x2​∈S2​}

如果 S 1 S_{1} S1​和 S 2 S_{2} S2​是凸集，那么 S 1 × S 2 S_{1}×S_{2} S1​×S2​也为凸集

线性矩阵不等式的解是凸的：我们称下式为线性矩阵不等式（LMI），其中 B , A i ∈ S m B,A_{i}\in S^{m} B,Ai​∈Sm

A ( x ) = x 1 A 1 + x 2 A 2 + . . . + x n A n ⪯ B A(x)=x_{1}A_{1}+x_{2}A_{2}+...+x_{n}A_{n}\preceq B A(x)=x1​A1​+x2​A2​+...+xn​An​⪯B

LMI的解集是凸集，即 { x ∥ A ( x ) ≤ B } \{x\| A(x) \leq B\} {x∥A(x)≤B}为凸集

透视变换：定义 P P P： R n + 1 → R n R^{n+1}\rightarrow R^{n} Rn+1→Rn（降维）， P ( z , t ) = z t P(z,t)=\frac{z}{t} P(z,t)=tz​为透视变换，其定义域为 P = R n × R + + ( z ∈ R n , t ∈ R + + ) P=R^{n}×R_{++}(z\in R^{n},t\in R_{++}) P=Rn×R++​(z∈Rn,t∈R++​)。透视变换对向量进行收缩（或称为规范化），使得最后一维向量为1并舍弃

透视变换保凸性：设有凸集合C= { ( x , t ) ∣ x ∈ R n , t > 0 } \{(x, t)| x\in \R^{n}, t>0\} {(x,t)∣x∈Rn,t>0}，其透视变换所得集合为 { x t ∣ x ∈ R n , t > 0 } \{\frac{x}{t}|x\in \R^{n}, t>0\} {tx​∣x∈Rn,t>0}，这个集合也是凸的。当然一个凸集在反透视变换下仍是凸的，即 { ( x , t ) ∈ R n + 1 ∣ x t ∈ C , t > 0 } \{(x,t)\in R^{n+1}| \frac{x}{t}\in C, t>0\} {(x,t)∈Rn+1∣tx​∈C,t>0}是凸的

关于透视变换保凸性可以这样理解：假设 n = 1 n=1 n=1，那么对应的就是一个二维向量向一维向量（标量）的透视，假定此二维向量为 ( x 1 , y 1 ) (x_{1}, y_{1}) (x1​,y1​)，代入透视变换（函数）进行计算，那么其结果就是 ( x 1 y 1 ) (\frac{x_{1}}{y_{1}}) (y1​x1​​)，如果将它前面加上符号，然后再扩充一个维度，就可以得到一个新的点 ( − x 1 y 1 ， − 1 ) (-\frac{x_{1}}{y_{1}}， -1) (−y1​x1​​，−1)。如下图，透视变换就好像把 ( x 1 , y 1 ) (x_{1}, y_{1}) (x1​,y1​)投影到了 y = − 1 y=-1 y=−1这块“幕布上”。这类似于小孔成像，所以如果原来的集合是凸的，成像后自然也是凸的

分式线性变换：分式线性变换是透视变换和仿射变换的复合变换

假设 g : R n → R m + 1 g:R^{n}\rightarrow R^{m+1} g:Rn→Rm+1是仿射变换

g ( x ) = ( A c T   ) x + ( b d   ) = ( A x + b c T x + d   ) g(x)=\begin{pmatrix} A \\ c^{T}\ \end{pmatrix}x+\begin{pmatrix} b \\ d\ \end{pmatrix}=\begin{pmatrix} Ax+b \\ c^{T}x+d\ \end{pmatrix} g(x)=(AcT ​)x+(bd ​)=(Ax+bcTx+d ​)

故 f : R n → R m f:R^{n}\rightarrow R^{m} f:Rn→Rm为分式线性变换

f ( x ) = A x + b c T x + d f(x)=\frac{Ax+b}{c^{T}x+d} f(x)=cTx+dAx+b​

分式线性变换的保凸性：仿射变换和透视变换都是保凸的，那么它们的组合分式线性变换自然也是保凸的。也即，若集合 { x ∣ x ∈ R n } \{x|x\in \R^{n}\} {x∣x∈Rn}是凸集，则其分式线性变换

f ( x ) = { A x + b c T x + d ∣ x ∈ R n , A ∈ R m × n , b ∈ R m , c ∈ R n , d ∈ R , c T x + d > 0 } f(x)=\{\frac{Ax+b}{c^{T}x+d}|x\in \R^{n}, A\in R^{m×n}, b\in R^{m},c\in R^{n},d\in\R,c^{T}x+d>0\} f(x)={cTx+dAx+b​∣x∈Rn,A∈Rm×n,b∈Rm,c∈Rn,d∈R,cTx+d>0}

也是凸集