解平方根算法(四种解法+层层深入+逐步简化) |
您所在的位置:网站首页 › 计算机算术公式 › 解平方根算法(四种解法+层层深入+逐步简化) |
解平方根算法(四种解法+层层深入+逐步简化)
|
专栏:
学习笔记
同一个问题可能存在多种不同的算法;不同算法的思路不同,在解题的效率上也有很大不同。
对于算法的设计,岂可不慎乎 !
☆解平方根算法一(趋近法)
对于输入一个任意实数 c ,输出c 的算术平方根 g。根据以往的常识,可能最先想到的就是采用趋近的方法来求解。 ① 先从0到c的区域里选出一个整数g1估计值,满足g1的平方小于c 并且 g1+1的平方大于c 的条件。 ② 以步长h增加g1,即g1=g1+h, 其中h 为设置的精度(下文代码设为0.00001),使其结果不断向精度解靠拢。 #include #include using namespace std; void square_root(double c) { int r=0; double g=0; for(int i=0;i c){ g=i-1; break; } } while(abs(g*g -c) > 0.0001){ //判断g^2-c是否在精度范围内 g+=0.00001; //g每次加固定步长,以逼近所求解 r+=1; printf("%d : g = %.5f\n",r,g); } } int main() { double c; cin>>c; square_root(c); return 0; }当我们输入9时它能很快算出3.00000 但是当我们输入10后: 1 : g=3.00001 2 : g=3.00002 . . . 16226 : g=3.16226 16227 : g=3.16227好家伙,这算法一下就变得非常糟糕了,如果把解的精度和步长缩小,那么运行时间太大了,因此我们必须换一种算法~ ☆解平方根算法二(二分法)二分法的字面意思就是“一分为二”的方法,其基本思想就是,每次将求解值域的区间减少一半,因此可以快速缩小搜索范围。将二分法运用在此题上,就是期望能快速的找到平方根精确值所在的区间。 #include using namespace std; void square_root(double c){ double r=0,g=c; int j=0; //记录循环步数 while(g-r>1e-8){ double mid=(g+r)/2; if(mid*mid > c) g=mid; //说明mid右边 都满足mid*mid>c,所以用g=mid,缩小取值范围 else r=mid; //和上面一样的道理 j+=1; printf("%d : %.7f\n",j,mid); } } int main() { double c; cin>>c; square_root(c); return 0; }我们这里输入c=10; 结果: 1 : 5.0000000 2 : 2.5000000 3 : 3.7500000 . . 25 : 3.1622776 26 : 3.1622778 27 : 3.1622777 28 : 3.1622777 29 : 3.1622777 30 : 3.1622777我们非常成功的将算法一的16227次循环简化到了30次循环,并且还大大提高了精确度 既然算法二已经如此的高效了,这是不是就意味着算法二即为平方根的最佳解法呢? 有趣的是,还可以进一步的修改算法,获得更少的循环次数,加快g 的求解过程,而且还能得到同样精度甚至更高的精度解。在算法中,要养成良好的思维习惯,持续不断的对设计进行优化,寻找更高效的解法,这也是计算机科学之美的重要体现~ ☆解平方根算法三(牛顿迭代法)因为要求c 的平方根,所以满足 x^2=c ,此时x 的解就是c 的平方根,因此不妨令f(x)=x^2-c,设x0为方程的解,即f(x0)=0。选取g0作为x0 的初始近似值,算法的核心在于如何推导下一个点g1 ,使得g1 更趋近于正确值x0. 以此类推直到找到精确范围内的正确解就行了。 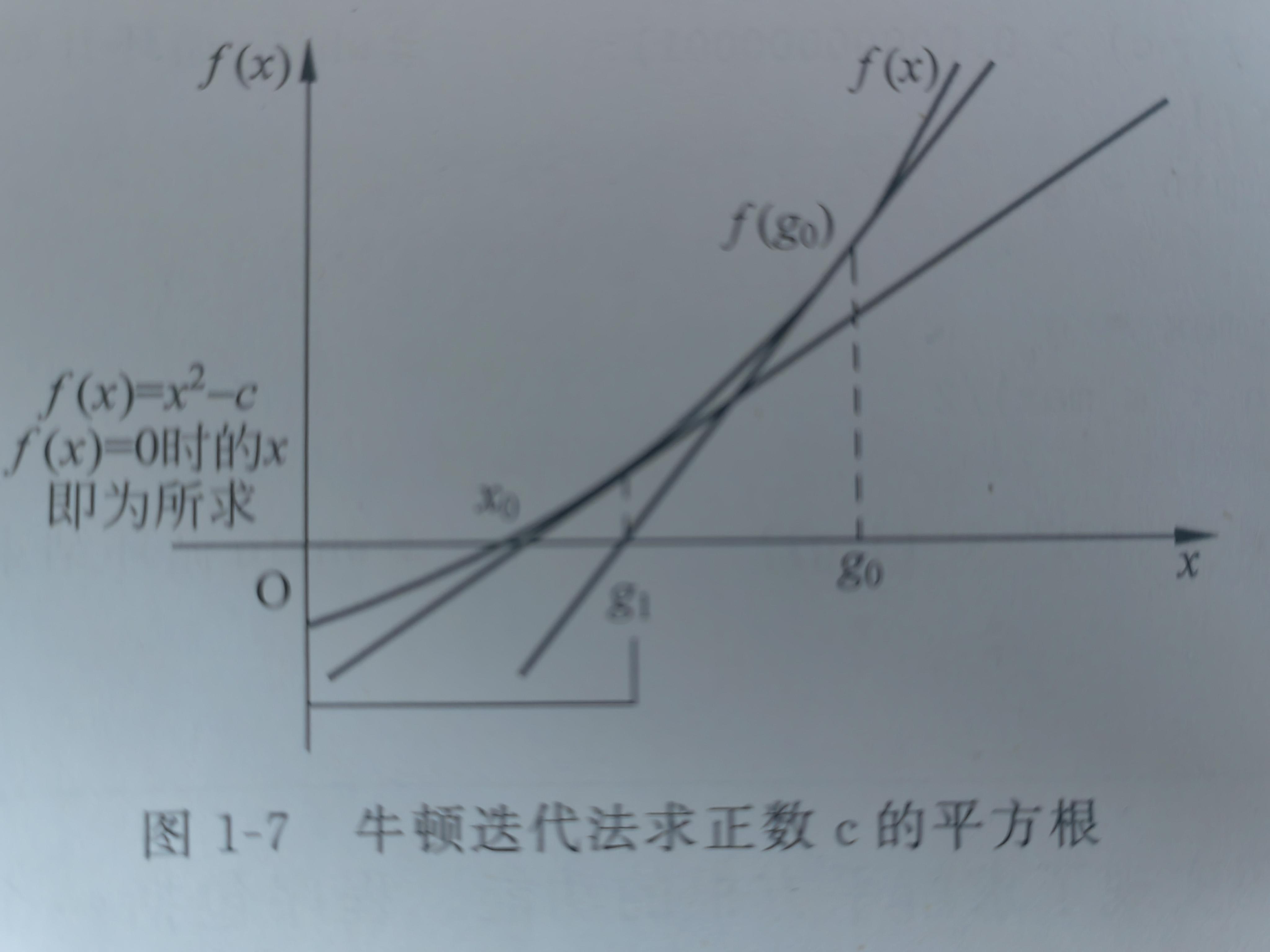
算法的思想就是:当x=g0 时,过点f(x) 做一条切线。这条切线与x 轴相交于一点,这个交点就是g1 。 从图1-7 可以清楚地看到g1 比 g0 更趋近于x0。 然后再经过f(g1)做一条切线,同样该切线与x轴的交点成为下一个更趋近于x0 的近似值g2.以此类推就行了~ 通过数学计算,可以得出g1 和g0 的关系是 g1=(g0+c / g0 ) / 2 对证明感兴趣的友友可以看一下: 过点(g0, f(g0))做f(x) 的切线 L ,f(x)的导数为2x ,所以 切线L 的斜率就是f '(g0)=2g0 。 然后就可以求L 的切线方程:y= f(g0) + f '(g0)( x - g0 ) ,设L和x 轴的交点坐标为(g1,0),则 0=f( g0 ) +f '( g0 )( g1- g0 ) 。因为f(g0 )= g0^2-c 且 f '(g0)=2g0 。将其带入计算化简,得到: g0^2 -c + 2g0( g1 - g0 )= 0 ,所以2g0g1=c-g0^2+2g0^2= c+g0^2 ,化简得到: g1=( g0 + c / g0 ) / 2以此类推,每次循环都将近似值用这个公式更新,就能快速得到c 的算术平方根~ #include #include using namespace std; void square_root(double c){ int j=0; //记录循环步数 double g=c/2; //先将g设为 区间中点, while(abs(g * g -c) >1e-11){ g=(g+c/g)/2; j+=1; printf("%d : %.10f\n",j,g); } } int main() { double c; cin>>c; square_root(c); return 0; }我们输入c=10 1 : 3.5000000000 2 : 3.1785714286 3 : 3.1623194222 4 : 3.1622776604 5 : 3.1622776602我们非常成功的将算法二的30次循环简化至5次循环,并且还大大提高了精确度,岂不美哉 !! ☆升级版牛顿迭代法到这里,我们可能会疑惑了,求平方根的 sqrt( )函数的底层算法效率的问题。 这里我也没办法讲清楚,看这篇博客sqrt()函数实现(底层探究) 你会看到这份“神一样”的代码:‘ float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed #ifndef Q3_VM #ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE? #endif #endif return y; }上述源代码解析: 点这里 当然我只能看出它本质上还是使用的牛顿迭代法,但真正看不懂的是 0x5f3759df86这个神一样的数字的由来,经过这一步计算(上面what the fuck那步),使得这个值非常接近1/sqrt(n),因此我们只需要2次牛顿迭代就可以达到我们所需要的精度,是真的六!!。 精简版: float InvSqrt(float x) { float xhalf = 0.5f*x; int i = *(int*)&x; // get bits for floating VALUE i = 0x5f375a86- (i>>1); // gives initial guess y0 x = *(float*)&i; // convert bits BACK to float x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy return x; } 运行效率:趋近法 < 二分法 < 普通牛顿迭代法 < sqrt()函数 < 升级版牛顿迭代法最后总结:解决同一个问题可以设计出各种不同的算法,不是获得解就结束了,而且要分析不同算法之间对于程序执行效率的影响,不同的算法会有很显著的性能优劣差异,岂可不慎乎!! References[1] 《计算机科学导论—以python为舟》 (沙行勉 著) [2] sqrt函数实现(神奇的算法) |
【本文地址】
今日新闻 |
推荐新闻 |