我们知道AES的加解密过程都可以用有限域中的计算表示出来。关于AES的加解密过程，很多教材资料都有详细描述，这里我想强调①关于AES加密过程中的MixColumn阶段是如何计算的；②AES的解密流程问题。 关于AES算法的全部代码可以看这个AES加解密算法全过程实现(C++)

我们经常会看到参考资料说AES的列混合过程是对状态矩阵的每一列左乘一个确定的矩阵(如下图)，一般表示为

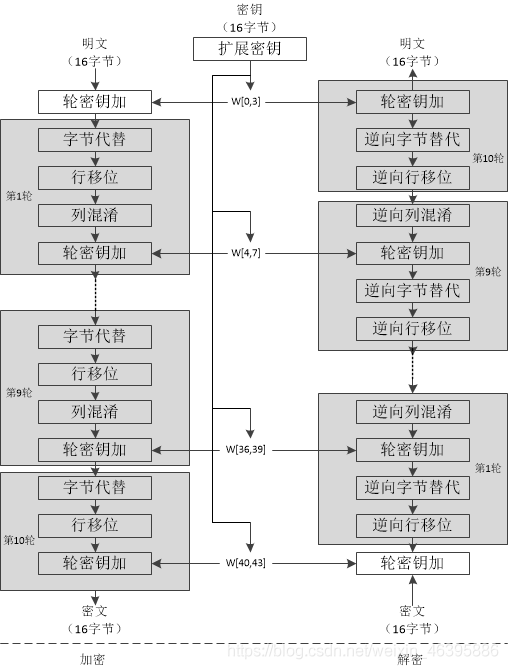
然后我们乘了之后会发现结果并不对。事实上，这里表示的并不是简单的矩阵乘法，而是 G F ( 2 8 ) GF(2^{8}) GF(28)上的多项式模乘。

列混合的定义是：MixColumn(State)是将状态矩阵的每一列看成 G F ( 2 8 ) GF(2^{8}) GF(28)上的一个多项式，且与一个固定的多项式 c ( x ) = { 03 } x 3 + { 01 } x 2 + { 01 } x + { 02 } c(x)=\lbrace 03\rbrace x^{3}+\lbrace 01\rbrace x^{2}+\lbrace 01\rbrace x+\lbrace 02\rbrace c(x)={03}x3+{01}x2+{01}x+{02}相乘后模 x 4 + 1 x^{4}+1 x4+1。例如：对于状态矩阵的某一列 ( a 0 a 1 a 2 a 3 ) \begin{pmatrix} a_{0} \\ a_{1}\\ a_{2}\\ a_{3} \end{pmatrix} ⎝⎜⎜⎛​a0​a1​a2​a3​​⎠⎟⎟⎞​ 看成多项式 a 3 x 3 + a 2 x 2 + a 1 x + a 0 a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0} a3​x3+a2​x2+a1​x+a0​，列混合就是计算 ( a 3 x 3 + a 2 x 2 + a 1 x + a 0 ) c ( x ) ( m o d ( x 4 + 1 ) ) (a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0})c(x)\pmod{(x^{4}+1)} (a3​x3+a2​x2+a1​x+a0​)c(x)(mod(x4+1))。这样的定义也才是符合"AES的加解密过程都可以用有限域中的计算表示出来"这句话嘛。

那问题来了，这个多项式相乘的计算怎么就成上述的矩阵形式？这就关乎 x 4 + 1 x^{4}+1 x4+1这个多项式了。对于任意 x i x^{i} xi，有 x i m o d ( x 4 + 1 ) = x i ( m o d 4 ) x^{i}mod(x^4+1)=x^{i\pmod{4}} ximod(x4+1)=xi(mod4)。例如： x 6 ≡ x 2 ( m o d x 4 + 1 ) x^{6}\equiv x^{2}\pmod{x^{4}+1} x6≡x2(modx4+1)。根据这个事实，我们可以计算多项式相乘再取模的结果（在计算时， x 6 x^{6} x6就等于 x 2 x^{2} x2， x 5 x^{5} x5就等于 x x x， x 4 x^{4} x4就等于1）： b 3 x 3 + b 2 x 2 + b 1 x + b 0 = ( a 3 x 3 + a 2 x 2 + a 1 x + a 0 ) ( { 03 } x 3 + { 01 } x 2 + { 01 } x + { 02 } ) = ( a 3 ∗ 03 ) x 6 + ( a 3 ∗ 01 + a 2 ∗ 03 ) x 5 + ( a 3 ∗ 01 + a 2 ∗ 01 + a 1 ∗ 03 ) x 4 + ( a 3 ∗ 02 + a 2 ∗ 01 + a 1 ∗ 01 + a 0 ∗ 03 ) x 3 + ( a 2 ∗ 02 + a 1 ∗ 01 + a 0 ∗ 01 ) x 2 + ( a 1 ∗ 02 + a 0 ∗ 01 ) x + a 0 ∗ 02 = ( a 3 ∗ 02 + a 2 ∗ 01 + a 1 ∗ 01 + a 0 ∗ 03 ) x 3 + ( a 3 ∗ 03 + a 2 ∗ 02 + a 1 ∗ 01 + a 0 ∗ 01 ) x 2 + ( a 3 ∗ 01 + a 2 ∗ 03 + a 1 ∗ 02 + a 0 ∗ 01 ) x + ( a 3 ∗ 01 + a 2 ∗ 01 + a 1 ∗ 03 + a 0 ∗ 02 ) b_{3}x^{3}+b_{2}x^{2}+b_{1}x+b_{0}=(a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0})(\lbrace 03\rbrace x^{3}+\lbrace 01\rbrace x^{2}+\lbrace 01\rbrace x+\lbrace 02\rbrace)=(a_{3}*03)x^{6}+(a_{3}*01+a_{2}*03)x^{5}+(a_{3}*01+a_{2}*01+a_{1}*03)x^{4}+(a_{3}*02+a_{2}*01+a_{1}*01+a_{0}*03)x^{3}+(a_{2}*02+a_{1}*01+a_{0}*01)x^{2}+(a_{1}*02+a_{0}*01)x+a_{0}*02\\ =(a_{3}*02+a_{2}*01+a_{1}*01+a_{0}*03)x^{3}+(a_{3}*03+a_{2}*02+a_{1}*01+a_{0}*01)x^{2}+(a_{3}*01+a_{2}*03+a_{1}*02+a_{0}*01)x+(a_{3}*01+a_{2}*01+a_{1}*03+a_{0}*02) b3​x3+b2​x2+b1​x+b0​=(a3​x3+a2​x2+a1​x+a0​)({03}x3+{01}x2+{01}x+{02})=(a3​∗03)x6+(a3​∗01+a2​∗03)x5+(a3​∗01+a2​∗01+a1​∗03)x4+(a3​∗02+a2​∗01+a1​∗01+a0​∗03)x3+(a2​∗02+a1​∗01+a0​∗01)x2+(a1​∗02+a0​∗01)x+a0​∗02=(a3​∗02+a2​∗01+a1​∗01+a0​∗03)x3+(a3​∗03+a2​∗02+a1​∗01+a0​∗01)x2+(a3​∗01+a2​∗03+a1​∗02+a0​∗01)x+(a3​∗01+a2​∗01+a1​∗03+a0​∗02) 把上述结果写成矩阵形式，不正是 ( b 0 b 1 b 2 b 3 ) = ( 02 03 01 01 01 02 03 01 01 01 02 03 03 01 01 02 ) ( a 0 a 1 a 2 a 3 ) \begin{pmatrix} b_{0}\\b_{1}\\b_{2}\\b_{3} \end{pmatrix}= \begin{pmatrix} 02 & 03 & 01 & 01\\ 01 & 02 & 03 & 01\\ 01 & 01 & 02 & 03\\ 03 & 01 & 01 & 02 \end{pmatrix} \begin{pmatrix} a_{0}\\a_{1}\\a_{2}\\a_{3} \end{pmatrix} ⎝⎜⎜⎛​b0​b1​b2​b3​​⎠⎟⎟⎞​=⎝⎜⎜⎛​02010103​03020101​01030201​01010302​⎠⎟⎟⎞​⎝⎜⎜⎛​a0​a1​a2​a3​​⎠⎟⎟⎞​ 所以现在你懂了这个矩阵式子表达的意思了吧。

那这个矩阵如何计算呢？对于上面的矩阵，我们有 b 0 = 02 ∗ a 0 + 03 ∗ a 1 + 01 ∗ a 2 + 01 ∗ a 3 b_{0}=02*a_{0}+03*a_{1}+01*a_{2}+01*a_{3} b0​=02∗a0​+03∗a1​+01∗a2​+01∗a3​。这里的02要转化成 G F ( 2 8 ) GF(2^{8}) GF(28)上的多项式 x x x。（因为02=00000010，写成多项式就是 x x x）同理，03，01和每个 a i a_{i} ai​都要写成 G F ( 2 8 ) GF(2^{8}) GF(28)上的多项式，乘法和加法都是模 m ( x ) = x 8 + x 4 + x 3 + x + 1 m(x)=x^{8}+x^{4}+x^{3}+x+1 m(x)=x8+x4+x3+x+1上的加法和乘法（这是AES选的 G F ( 2 8 ) GF(2^{8}) GF(28)上的不可约多项式）。

模 m ( x ) m(x) m(x)的加法很简单，就直接异或。乘法计算就比较复杂了。其实多项式相乘本就比较麻烦，这里还要模 m ( x ) m(x) m(x)，而且这个 m ( x ) m(x) m(x)很不友好，不像模 ( x 4 + 1 ) (x^{4}+1) (x4+1)那么有特点，所以这个多项式模乘需要寻找更好的方法。这里就介绍一种较为方便的方法。我们观察上面的矩阵，发现每个 a i a_{i} ai​只需乘01、02、03这3个数，并不用乘其他数，所以只要知道如何乘01，02，03即可。

01表示成多项式就是1，对任何 a i a_{i} ai​， 01 ∗ a i = a i 01*a_{i}=a_{i} 01∗ai​=ai​，再模 m ( x ) m(x) m(x)依旧是 a i a_{i} ai​。

02表示多项式 x x x，对任何 a i a_{i} ai​， a i ∗ 02 ( m o d m ( x ) ) a_{i}*02\pmod{m(x)} ai​∗02(modm(x))相当于先把 a i a_{i} ai​表示的二进制串左移1位。移位后，若首位上是1，则再将该二进制串的后8位异或0x1b得到结果；若首位上是0，取后8位就是结果。例如： a = 0 x 23 a=0x23 a=0x23， 转化乘二进制就是00100011， 0 x 23 ∗ 0 x 02 0x23*0x02 0x23∗0x02应该这么计算：先左移1位成为001000110，首位（最左边）上是0，所以后8位01000110=0x46就是结果。再如 a = 0 x a 3 a=0xa3 a=0xa3，转化成二进制是10100011，计算 0 x a 3 ∗ 0 x 02 0xa3*0x02 0xa3∗0x02：左移一位得101000110，首位是1，则取后8位异或0x1b得01011101，即0x5d。

为什么是这样算？很简单，由于02表示多项式x， a i ∗ 02 a_{i}*02 ai​∗02相当于 a i a_{i} ai​的多项式乘x，也就是多项式系数不变，每一项次数加1，这不就是相当于左移一位嘛。再一步，要模 m ( x ) = x 8 + x 4 + x 3 + x + 1 m(x)=x^{8}+x^{4}+x^{3}+x+1 m(x)=x8+x4+x3+x+1：如果乘完之后的多项式次数小于8，就不用模了，这就是上面说的首位为0的情况；如果乘完之后多项式次数等于8，就要模 m ( x ) m(x) m(x)，但是稍加分析会发现此时的多项式一定是小于 2 m ( x ) 2m(x) 2m(x)，所以模 m ( x ) m(x) m(x)的余式就相当于减 m ( x ) m(x) m(x)的结果，我们知道， G F ( 2 8 ) GF(2^{8}) GF(28)上的减就是异或， m ( x ) m(x) m(x)的后8位表示成16进制就是0x1b，所以异或0x1b，此时对应着上面的首位是1的情况

知道了01和02的乘法，03=01+02，可以利用分配律计算出03。

例如： 03 × a 3 = ( 01 + 02 ) × a 3 = 01 × a 3 + 02 × a 3 = a 3 + 5 d = f e 03\times a3=(01+02)\times a3=01\times a3+02\times a3=a3+5d=fe 03×a3=(01+02)×a3=01×a3+02×a3=a3+5d=fe.

在AES解密的时候，也可以通过这种方法计算。

我们知道加密过程每一轮的轮函数包括：字节替换、行移位、列混合、轮密钥加，并且顺序是固定的。需要指出的是，解密时的轮函数的顺序是：逆行移位、逆字节替换、轮密钥加、逆列混合。如果不理解的看下图便很明白！ 参考： AES加解密算法详解