手动求导，顾名思义，通过求导的一些公式，我们提前算好导数表达式，再带入公式求解。 假设我们以一个输入为3个变量的函数 f f f为例： f ( x 1 , x 2 , x 3 ) = 3 ∗ ( x 1 2 + x 2 ∗ x 3 ) f(x_1, x_2, x_3) = 3*(x_1^2+x_2*x_3) f(x1​,x2​,x3​)=3∗(x12​+x2​∗x3​) 我们定义输入的三个值为 （ x 1 = 2 , x 2 = 3 , x 3 = 4 ） （x_1=2, x_2=3, x_3=4） （x1​=2,x2​=3,x3​=4），那手动微分是怎么计算？首先，分别对 x 1 , x 2 , x 3 x_1, x_2, x_3 x1​,x2​,x3​求导，再带入输入值，得到如下结果： ∂ f ( x 1 , x 2 , x 3 ) ∂ x 1 = 3 ∗ 2 ∗ x 1 = 12 \frac{\partial f(x_1, x_2, x_3)}{\partial x_1} = 3*2*x_1 = 12 ∂x1​∂f(x1​,x2​,x3​)​=3∗2∗x1​=12 ∂ f ( x 1 , x 2 , x 3 ) ∂ x 2 = 3 ∗ x 3 = 12 \frac{\partial f(x_1, x_2, x_3)}{\partial x_2} = 3*x_3 = 12 ∂x2​∂f(x1​,x2​,x3​)​=3∗x3​=12 ∂ f ( x 1 , x 2 , x 3 ) ∂ x 3 = 3 ∗ x 2 = 9 \frac{\partial f(x_1, x_2, x_3)}{\partial x_3} = 3*x_2 = 9 ∂x3​∂f(x1​,x2​,x3​)​=3∗x2​=9

符号微分通过求导规则来计算导数值，给定一个函数，通过规则一步一步求解，常见的求导规则有如下：

d ( f + g ) d x = d f d x + d g d x \frac{d(f+g)}{dx} = \frac{df}{dx} + \frac{dg}{dx} dxd(f+g)​=dxdf​+dxdg​

符号微分的主要缺陷就是：

数值微分主要基于导数的极限定义，例如给定一个多元函数 f : R n → R f: R^n \to R f:Rn→R，我们可以估计函数梯度 ∇ f = ( ∂ f ∂ x 1 , . . . , ∂ f ∂ x n ) \nabla f = (\frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n}) ∇f=(∂x1​∂f​,...,∂xn​∂f​)公式如下： ∂ f ( x ) ∂ x i ≈ lim ⁡ h → 0 f ( x + h e i ) − f ( x ) h \frac{\partial f(x)}{\partial x_i} \approx \lim_{h \to 0} \frac{f(x+he_i)-f(x)}{h} ∂xi​∂f(x)​≈h→0lim​hf(x+hei​)−f(x)​ 为了避免截断误差，一般使用中心差分，如下公式： ∂ f ( x ) ∂ x i ≈ lim ⁡ h → 0 f ( x + h e i ) − f ( x − h e i ) 2 h \frac{\partial f(x)}{\partial x_i} \approx \lim_{h \to 0}\frac{f(x+he_i)-f(x-he_i)}{2h} ∂xi​∂f(x)​≈h→0lim​2hf(x+hei​)−f(x−hei​)​ h h h是一个很小的数，一般设置为 h = 1 e − 6 h=1e-6 h=1e−6

自动微分是一个有效的计算偏导方法，对任意函数的一点，自动微分可以自动计算偏导数。自动微分有两种计算方式：前向模式和反向模式，接下来我们用函数 f ( x 1 , x 2 ) = l n ( x 1 ) + x 1 x 2 − s i n ( x 2 ) f(x_1, x_2) = ln(x_1) + x_1x_2 - sin(x_2) f(x1​,x2​)=ln(x1​)+x1​x2​−sin(x2​)为例，分别对自动微分的前向模式和方向模式做一个对比。

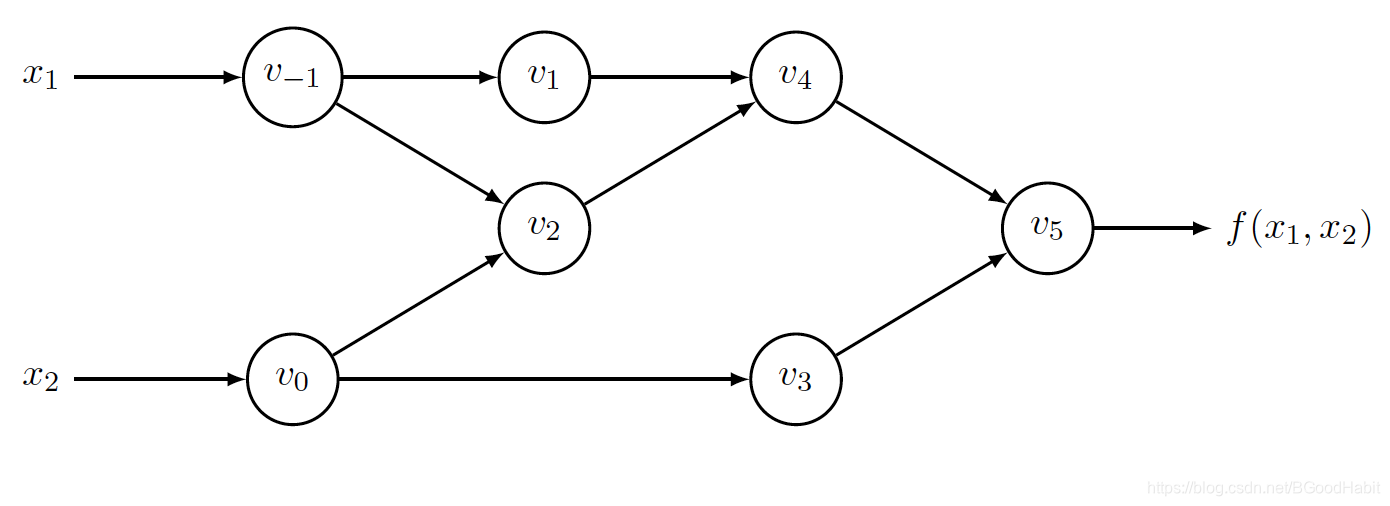
对函数 f ( x 1 , x 2 ) = l n ( x 1 ) + x 1 x 2 − s i n ( x 2 ) f(x_1, x_2) = ln(x_1) + x_1x_2 - sin(x_2) f(x1​,x2​)=ln(x1​)+x1​x2​−sin(x2​)构造图如下： 每个中间变量 v i v_i vi​，计算对 x 1 x_1 x1​的偏导数记做： v ˙ = ∂ v i ∂ x 1 v˙= \frac{\partial v_i}{\partial x_1} v˙=∂x1​∂vi​​ 接下来，我们看自动微分的前向模式计算细节，我们按照输入 ( x 1 , x 2 ) = ( 2 , 5 ) (x_1, x_2)=(2,5) (x1​,x2​)=(2,5)为例：

自动微分的反向模式通过从输出反向计算各变量的偏导数，我们定义变量 v ‾ i = ∂ y j ∂ v i \overline{v}_i = \frac{\partial y_j}{\partial v_i} vi​=∂vi​∂yj​​，还是回到例子 y = f ( x 1 , x 2 ) = l n ( x 1 ) + x 1 x 2 − s i n ( x 2 ) y=f(x_1,x_2)=ln(x_1) + x_1x_2 - sin(x_2) y=f(x1​,x2​)=ln(x1​)+x1​x2​−sin(x2​)，从上述构造的图可以看出，变量 v 0 v_0 v0​通过影响 v 2 和 v 3 v_2和v_3 v2​和v3​来影响 y y y，所以， v 0 v_0 v0​对 y y y影响可以通过如下公式计算： ∂ y ∂ v 0 = ∂ y ∂ v 2 ∂ v 2 ∂ v 0 + ∂ y ∂ v 3 ∂ v 3 ∂ v 0 \frac{\partial y}{\partial v_0} = \frac{\partial y}{\partial v_2}\frac{\partial v_2}{\partial v_0}+\frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_0} ∂v0​∂y​=∂v2​∂y​∂v0​∂v2​​+∂v3​∂y​∂v0​∂v3​​ 或者 v 0 ‾ = v 2 ‾ ∂ v 2 ∂ v 0 + v 3 ‾ ∂ v 3 ∂ v 0 \overline{v_0} = \overline{v_2}\frac{\partial v_2}{\partial v_0}+\overline{v_3}\frac{\partial v_3}{\partial v_0} v0​​=v2​​∂v0​∂v2​​+v3​​∂v0​∂v3​​ 在反向模式里，我们首先以 v 5 ‾ = y ‾ = ∂ y ∂ y = 1 \overline{v_5}=\overline{y}=\frac{\partial y}{\partial y}=1 v5​​=y​=∂y∂y​=1开始，在最后我们得到 ∂ y ∂ x 1 = x 1 ‾ 和 ∂ y ∂ x 2 = x 2 ‾ \frac{\partial y}{\partial x_1}=\overline{x_1} 和 \frac{\partial y}{\partial x_2}=\overline{x_2} ∂x1​∂y​=x1​​和∂x2​∂y​=x2​​，只需要一次反向计算。 相对前向模式，反向模式最大的优势是需要更少的计算，对于函数 f : R n → R f: R^n \to R f:Rn→R这样有 n n n个输入，反向模式只需要一次计算就可以得到所有的梯度 ∇ f = ( ∂ y ∂ x 1 , . . . , ∂ y ∂ x n ) \nabla f = (\frac{\partial y}{\partial x_1},...,\frac{\partial y}{\partial x_n}) ∇f=(∂x1​∂y​,...,∂xn​∂y​)，而前向计算需要算 n n n次前向计算。我们来看下在反向计算函数 f ( x 1 , x 2 ) f(x_1,x_2) f(x1​,x2​)过程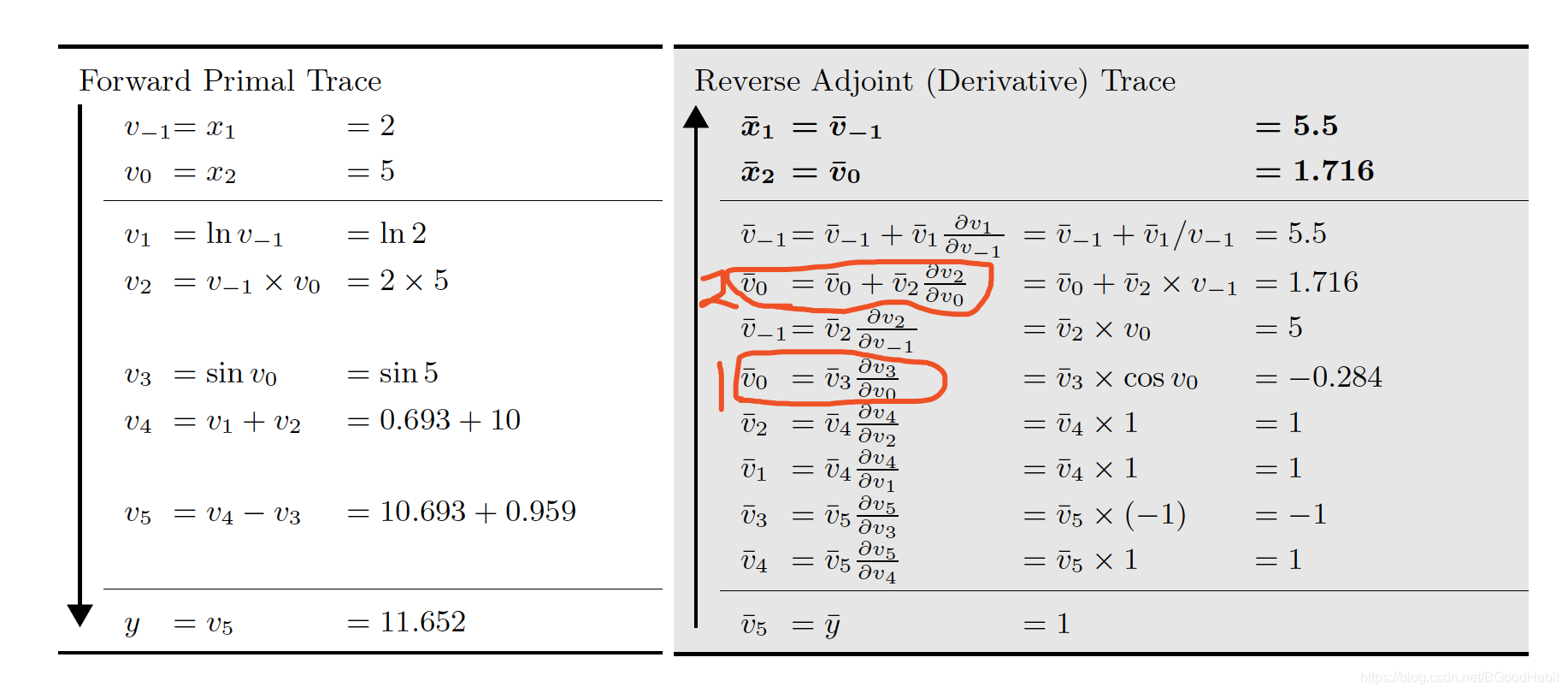

从下往上计算，其中 v 5 ‾ , v 4 ‾ , v 3 ‾ , v 1 ‾ , v 2 ‾ \overline{v_5}, \overline{v_4}, \overline{v_3}, \overline{v_1}, \overline{v_2} v5​​,v4​​,v3​​,v1​​,v2​​计算很容易求解得到，接下来我们来看 v 0 ‾ \overline{v_0} v0​​的计算，首先从构造的图来看， v 0 v_0 v0​作用于 v 3 v_3 v3​和 v 2 v_2 v2​, 而 v 3 = sin ⁡ v 0 v_3 = \sin{v_0} v3​=sinv0​，所以在反向模式里，如上图所示，标红的第一次计算 v 0 ‾ = ∂ y ∂ v 3 ∂ v 3 ∂ v 0 = v 3 ‾ ∂ v 3 ∂ v 0 \overline{v_0}=\frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_0}=\overline{v_3}\frac{\partial v_3}{\partial v_0} v0​​=∂v3​∂y​∂v0​∂v3​​=v3​​∂v0​∂v3​​，第二次计算 v 0 ‾ = ∂ y ∂ v 3 ∂ v 3 ∂ v 0 + ∂ y ∂ v 2 ∂ v 2 ∂ v 0 = v 0 ‾ + v 2 ‾ ∂ v 2 ∂ v 0 \overline{v_0}=\frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_0}+\frac{\partial y}{\partial v_2}\frac{\partial v_2}{\partial v_0}=\overline{v_0}+\overline{v_2}\frac{\partial v_2}{\partial v_0} v0​​=∂v3​∂y​∂v0​∂v3​​+∂v2​∂y​∂v0​∂v2​​=v0​​+v2​​∂v0​∂v2​​，同理，可得到 v ‾ − 1 \overline{v}_{-1} v−1​的结果

对于一个函数 f : R n → R m f : R^n \to R^m f:Rn→Rm，假设计算函数 f f f的所有operation操作总和记做 o p s ( f ) ops(f) ops(f)，则计算一个 m × n m×n m×n的雅可比导数矩阵，自动微分的前向计算需要 n c nc nc次 o p s ( f ) ops(f) ops(f)操作，反向模式需要 m c mc mc次 o p s ( f ) ops(f) ops(f)操作，其中 c < 6 c < 6 c