线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

您所在的位置：网站首页 › 角度大小的表示方法 › 线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

2024-07-09 23:42| 来源: 网络整理| 查看: 265

0 参考的知识点和目录

1 向量

1.1 向量的概念

1.2 向量如何表示

1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段

2 矩阵

2.1 矩阵就是多个列向量的集合/合并（& 而不是 +），矩阵就是多个列向量的一种简化书写方式？

2.2 矩阵的加法 =等价于= 向量的加法

2.3 矩阵的数乘 =等价于= 向量的数乘

2.4 矩阵的点乘 =等价于= 列向量（或者行向量）的点乘

3 矩阵的特点

3.1 矩阵里不同位置的元素，影响范围是指定的有规律的

3.1.1 矩阵里数字的位置和影响范围

3.2 矩阵的本质是旋转和缩放

3.2.1 各种缩放/旋转的矩阵效果

3.2.2 矩阵里数字的效果

0 参考的知识点和目录

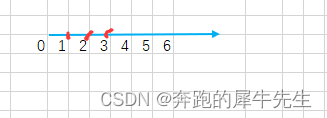
1 向量 1.1 向量的概念向量/数组：一组有序的数对应概念标量/数：一个数字，单个的数

1.2 向量如何表示

常规的代数表示方法

比如，这样的向量 [1,5] [1,2,3] [1,3,5,7,9]

一维的几何方法表示

一般的表示方法就是代数表示方法，基本就是原样列举： [1,2,3] 和 [1,3,2] 几何表示，比如用坐标轴上的点，表示向量/数组中的多个数字元素。但是这好像没啥意义，只是简单的用一条线上的不同点，表示了这个离散的数组，而且在坐标轴上还看不出来次序呢。比如下图，[1,2,3] 和 [1,3,2] 就不好区分

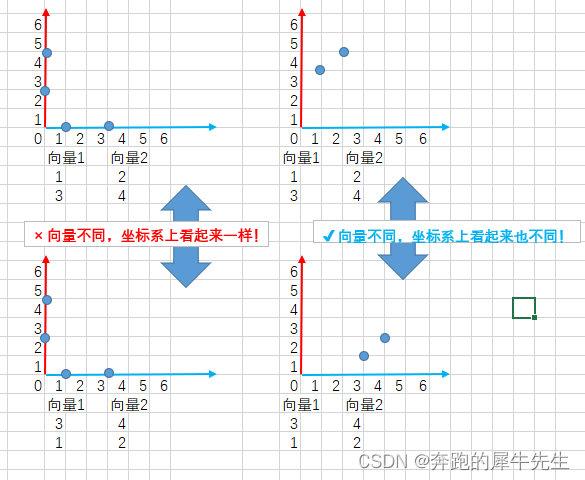
二维的坐标轴表示

如果是2维的，比如是2个向量呢用一根数量轴表示，全叠一起了，更不行把比如表示1个2维向量 [1,3]比如表示2个2维向量 [1,3] 和 [2,4]比如表示2个2维向量 [3,1] 和 [4,2]

方式1：

如果把1个向量的全部元素全部标记在1个坐标轴上，不但有时候没法区分1个向量，有时候也无法区别2个向量。

方式2：

如果把1个向量的不同元素，映射为不同坐标轴上的点，那么向量本身就是成用多个坐标轴表示的一个有向线段。这个有向线段，起点永远是原点，终点就是向量坐标（向量的元素）只要向量的元素，或元素排序不同，最终向量的图形显示就会不同！显然这个表示方法更好！

1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段

所以数学家们选的这个向量表示方法确实很巧妙，向量空间=张成空间

向量空间必须有原点所有的向量都从原点出发每个向量都是起点是原点，终点就是向量坐标（向量的元素）的一条有向线段简化来看，终点（终点的坐标组）其实就可以代表向量了

2 矩阵=向量组

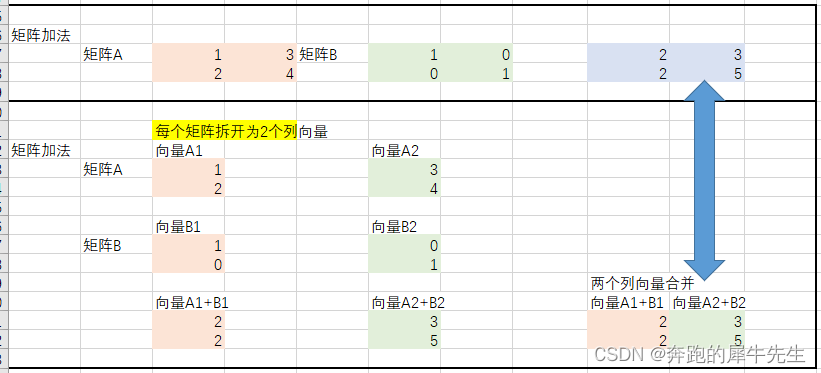
某些场合，列向量可以基本等价于行向量。乘法时不行。

矩阵就是多个列向量的集合矩阵就是向量组矩阵就是多个列向量的简要写法矩阵完全可以拆分为多个列向量，只能用拆分为多个列向量的方法反之，列向量可以合并为矩阵,只能用 and这种符号因为矩阵 = 列向量1 & 列向量2 & ..... 按顺序从左到右合并的关系，而不是向量相加的关系

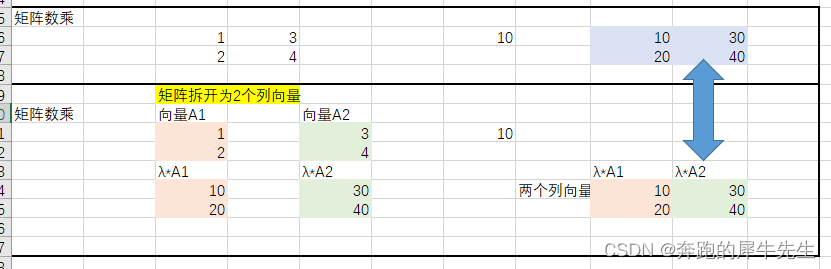
$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} = \begin{bmatrix} a11 \\ a21 \end{bmatrix} and \begin{bmatrix} a12 \\ a22\end{bmatrix}$

但是只能用合并/and 来形容，而不能用加法来形如多向量合并为矩阵这个过程

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} = \begin{bmatrix} a11 \\ a21 \end{bmatrix} + (?) \begin{bmatrix} a12 \\ a22\end{bmatrix}$

矩阵 ≠ 列向量1 & 列向量2 & .....

矩阵 ≠ 列向量1+列向量2+ .....

2.1 矩阵就是多个列向量的集合/合并（& 而不是 +），矩阵就是多个列向量的一种简化书写方式？对，矩阵就是向量组

矩阵的列向量

矩阵的每一列向量都代表这个方向的基底ei 走到了对应列向量的位置。比如这个矩阵 $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ ，它实际是 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 和 $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$ 这2个列向量组成的。第1个列向量 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 是第1个列向量对应的基 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ，伸缩旋转到 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 的位置第2个列向量 $\begin{bmatrix} 2\\ 4 \end{bmatrix}$ 是第2个列向量对应的基 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ ，伸缩旋转到 $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$ 的位置

2.2 矩阵的加法 =等价于= 向量的加法

简化书写，浓缩书写

矩阵是把多个列向量写在一起的简化形式也就是说以下是等价的：如果把矩阵拆为多个列向量矩阵相加，等于多个列向量分别相加后，再次合并为矩阵

2.3 矩阵的数乘 =等价于= 向量的数乘如果把矩阵拆为多个列向量矩阵标量乘法，等于多个列向量分别标量相乘后，再次合并为矩阵

2.4 矩阵的点乘 =等价于= 列向量（或者行向量）的点乘矩阵的乘法，要特别注意，左乘和右乘下面是AX=b的情况需要把A拆为列向量矩阵乘法和列向量乘法是等价的

下面是XA=b的情况需要把A拆为行向量（反正要灵活一点）矩阵乘法和这里拆的行向量乘法也是等价的

3 矩阵的特点 3.1 矩阵里不同位置的元素，影响范围是指定的有规律的 3.1.1 矩阵里数字的位置和影响范围矩阵里的数字的位置矩阵拆分为列向量

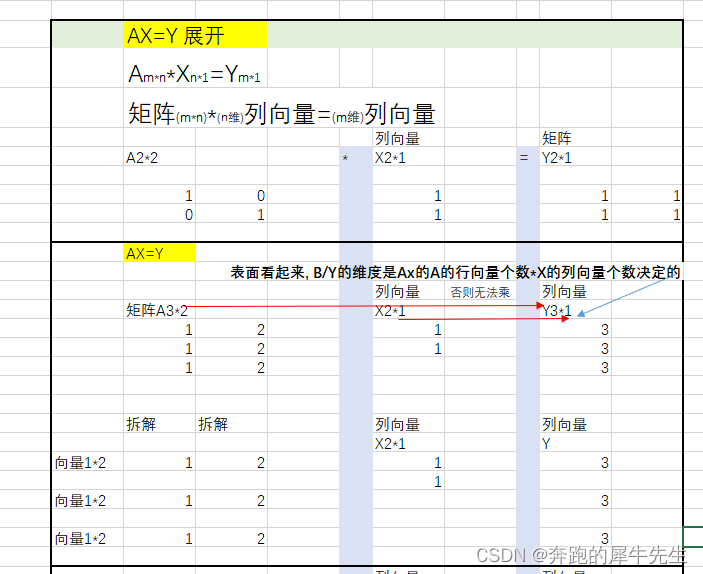
比如如果是 A*X=Y, x左乘矩阵A

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} * X=Y$

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} * \begin{bmatrix} b11 & b12 \\ b21 & b22\end{bmatrix} = \begin{bmatrix} a11*b11+a12*b21 & a11*b12+a12*b22 \\ a21*b11+a22*b21 & a21*b12+a22*b22\end{bmatrix}$

展开下

位置在a11的元素，会影响矩阵结果的，第1行第1个元素，第2个元素位置在a12的元素，会影响矩阵结果的，第1行第1个元素，第2个元素总结：第1行元素a11,a12 只会影响结果矩阵的第1行的内容位置在a21的元素，会影响矩阵结果的，第2行第1个元素，第2个元素位置在a22的元素，会影响矩阵结果的，第2行第1个元素，第2个元素总结：第2行元素a11,a12 只会影响结果矩阵的第2行的内容

所以

总结：矩阵A第1行元素只会影响结果矩阵Y(或b)的第1行的内容总结：矩阵A第2行元素只会影响结果矩阵Y(或b)的第2行的内容

$A*X=Y\rightarrow \begin{bmatrix} 2 & 0 \\ 0 & 3\end{bmatrix} *X=Y \rightarrow \begin{bmatrix} 2 & 0 \\ 0 & 3\end{bmatrix} *\begin{bmatrix} b11 & b12 \\ b21 & b22\end{bmatrix} =\begin{bmatrix} 2*b11 & 2*b12 \\ 3*b21 & 3*b22\end{bmatrix}$

A矩阵左上角2,只会影响b11 和b12A矩阵右下角3,只会影响b21 和b22

3.2 矩阵的本质是旋转和缩放 3.2.1 各种缩放/旋转的矩阵效果参考前面总结得各种特殊矩阵

线性代数的学习和整理7：各种特殊效果矩阵汇总_奔跑的犀牛先生的博客-CSDN博客行向量列向量[ 1 00 1]应该很多种把[ 1 00 2][ 5 01 0][] 零矩阵正交矩阵。https://blog.csdn.net/xuemanqianshan/article/details/132390306?spm=1001.2014.3001.5502

3.2.2 矩阵里数字的效果矩阵里的数字0矩阵里的数字1，表示不进行缩放矩阵里的数字2等，表示缩放矩阵里的数字-3 表示缩放-3倍，并且反向

比如下面这个矩阵：单位矩阵，单位矩阵如果放左边，就是表示对矩阵的第1行元素*1，对第2行元素*1，其实就是什么都不做。

1 0

0 1

【本文地址】

线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

今日新闻

推荐新闻

线性代数的学习和整理6：如何表示向量/矩阵？ 矩阵就是向量组，矩阵的本质是什么？

线性代数的学习和整理6：如何表示向量/矩阵？ 矩阵就是向量组，矩阵的本质是什么？

今日新闻

推荐新闻

线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？