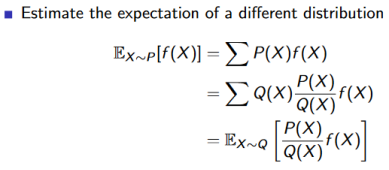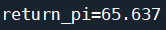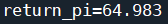强化学习 |
您所在的位置:网站首页 › 蒙特卡洛方法例题 › 强化学习 |
强化学习
|
参考: (1)强化学习(第二版) (2)强化学习精要-核心算法与TensorFlow实现 (3)https://www.cnblogs.com/pinard/p/9492980.html (4)https://deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver 一、蒙特卡洛(MC)方法 无论是在策略迭代还是在价值迭代中,都利用了状态转移概率来求解价值函数,并根据价值函数来寻找最优策略。我们将知道状态转移概率的问题称为“基于模型”的问题(Model-based Problem)。但是,在很多问题当中,我们是无法获得状态转移概率信息的,将这类型的问题称为“无模型”问题(Model-free Problem)。蒙特卡洛算法就是用于解决“无模型”问题,其思想和GPI(广义策略迭代)相同,包括策略评估和策略改进两个部分。 2、蒙特卡洛预测 给定一个策略,在不知道状态转移概率的情况下,蒙特卡洛算法是如何来学习其价值函数的呢?那就是通过经验。我们知道一个状态的价值是从该状态开始的期望回报,即未来的折扣收益累积值的期望。一个很自然的想法就是对所有经过这个状态之后产生的回报进行平均。随着越来越多的回报被观察到,根据大数定律,该平均值就会收敛于期望值,我们就用这种方法来估计价值函数。由于只通过状态价值函数我们是无法进行后期的策略改进的(因为不知道状态转移概率),所以我们实际上的估计目标是动作价值函数。 这里涉及到两种估计方法:(1)首次访问型MC预测算法(first-visit)。(2)每次访问型MC预测算法(every-visit)。 下面对这两种方法进行解释: 假设给定在策略$\pi$下的多幕数据,在每幕数据中每次状态-动作对(s,a)的出现都称为对(s,a)的一次访问。当然,在同一幕中(s,a)可能会被多次访问到。在这种情况下,我们称(s,a)的第一次访问为首次访问。首次访问型MC算法用(s,a)在所有幕中首次访问的回报的平均值估计$q_{\pi}\left(s,a\right)$,而每次访问型MC算法则用(s,a)在所有幕中所有访问的回报的平均值估计$q_{\pi}\left(s,a\right)$。 两种方法的比较:当(s,a)的访问次数足够多时,两种方法都能收敛,首次访问方法获得的(s,a)的价值函数方差较小,比每次访问方法收敛得更快。但当幕数较少时,每次访问方法可能会获得更好的效果。 下面是首次访问型MC预测算法:
为了节省存储量,在遍历每一幕时,我们使用增量式的更新方法来计算均值:$Q(s,a)=Q(s,a)+\frac{1}{N(s,a)}\left( G_{t}-Q(s,a) \right)$ 增量式更新的推导过程:$\mu_{k}=\frac{1}{k}\sum_{j=k}^{k}{x_{j}}=\frac{1}{k}\left( x_{k} + \sum_{j=1}^{k-1}{x_{j}} \right)=\frac{1}{k}\left( x_{k}+\left( k-1 \right)\mu_{k-1} \right)=\mu_{k-1}+\frac{1}{k}\left( x_{k}-\mu_{k-1} \right)$ 现在,我们考虑一个问题,如果采用确定性策略,那么一些(s,a)可能永远不会被访问到,也就无法根据经验改善$q_{\pi}\left( s,a \right)$的估计。这会不利于我们找到最优策略。因此,我们提出试探性出发假设,即每个(s,a)都有非零的概率可以作为一幕的起点,这样就保证了在采样的幕个数趋向于无穷的时候,每一个(s,a)都会被访问到无数次。可以看出,在试探性出发假设中还隐含了另一个假设,即无限幕假设。我们之所以提出这两个假设就是为了保证对于任意的$\pi$,蒙特卡洛算法都能精确地计算对应的$q_{\pi}$。 3、蒙特卡洛控制
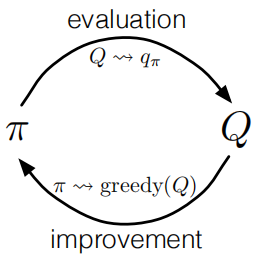
如上图所示,这是经典策略迭代流程,蒙特卡洛算法也可以使用这种方法。根据上文我们提出的两个很强的假设,可以保证蒙特卡罗算法的最终收敛。但是在实际操作中,我们是无法实现这两个假设的,因此,为了得到可行的算法,必须想办法去掉这两个假设。 首先,我们来设法去掉无限幕假设:(1)在每次策略评估中尽量确保对$q_{\pi}$的逼近。可以设置一个较小的误差值来作为判定标准(这一想法在策略迭代的算法实现中已经有所体现)。(2)不再追求$q_{\pi}$的收敛。我们可以在$q_{\pi}$尚未收敛的情况下进行策略评估。这种思想在GPI中已经提及到了。对于蒙特卡洛算法来说,自然可以逐幕交替进行评估与改进。 下面是基于试探性出发的蒙特卡洛算法(蒙特卡洛ES算法):
然后,我们来设法去掉试探性出发假设:(1)同轨策略方法(on-policy)。(2)离轨策略方法(off-policy)。 下面来详细介绍这两种方法: (1)同轨策略方法 在同轨策略中,用于生成采样数据序列的策略和用于实际决策的待改进的策略是相同的。其实,我们上面提到的蒙特卡洛ES算法就是同轨策略方法的一个例子。现在,我们要提出一个不再依赖试探性出发假设的同轨策略的蒙特卡洛控制方法。即在同轨策略方法中,我们使用“软性”策略。“软性”策略是指,对于任意$s\in \mathcal{S}$以及$a\in \mathcal{A}$,都有$\pi\left( a|s \right)>0$,但它们会逐渐地逼近一个确定性策略。在具体算法实现当中,我们使用$\epsilon-$贪心策略,即选择非贪心动作的概率为$\frac{\epsilon}{\left| \mathcal{A}\left( s \right) \right|}$,选择贪心动作的概率为$1-\epsilon+\frac{\epsilon}{\left| \mathcal{A}\left( s \right) \right|}$。这种策略既保证了对(s,a)的探索又尽可能地靠近了贪心策略。 下面是同轨策略的首次访问型MC控制算法:
(2)离轨策略方法 在同轨策略中,用于生成采样数据序列的策略和用于实际决策的待改进的策略是不同的。用来学习的策略称为目标策略($\pi$),用来生成行动样本的策略称为行动策略(b)。这样分离的好处在于当行动策略能对所有可能的动作进行采样时,目标策略可以使用确定策略(例如贪心策略)。 为了使用从b得到的多幕样本序列去预测$\pi$,我们要求在$\pi$下发生的每个动作都至少偶尔能在b下发生。换句话说,对于任意$\pi\left( a|s \right)>0$,要求$b\left( a|s \right)>0$。我们称其为覆盖假设。 因为要在一个分布(b)下去估计另一个分布($\pi$)的期望回报,所以我们引入重要性采样。 什么是重要性采样? 我们希望能够得到定义在服从P分布的X上的函数f(X)的期望,但是我们无法直接从P分布上进行采样,因此,我们引入另一个Q分布,从Q分布上进行采样,从而间接地求出f(X)在P分布上的期望。
当我们在Q分布上采样$\{ x_1,x_2,...,x_N \}$后,可以估计f(X)的期望,$E_{X\sim P}[f(X)]=\frac{1}{N}\sum_i^N{\frac{P\left( x_i \right)}{Q\left( x_i \right)}f\left( x_i \right)}$。其中$w^i=\frac{P\left( x_i \right)}{Q\left( x_i \right)}$称为重要性权重。这种方法称为普通重要性采样。还有一种方法称为加权重要性采样,即$E_{X\sim P}[f(X)]= \sum_i^N{\frac{w^i}{\sum_j^N{w^j}}f\left( x_i \right)}$。 这两种方法的区别在于: 普通重要性采样是真实期望的无偏估计,但是在P分布和Q分布相差较大时,会导致$\frac{P\left( x_i \right)}{Q\left( x_i \right)}f\left( x_i \right)$的方差较大,难以收敛。 加权重要性采样是真实期望的有偏估计,但是降低了$\frac{P\left( x_i \right)}{Q\left( x_i \right)}f\left( x_i \right)$的方差,易于收敛。 重要性采样在离轨策略中的应用: 在行动策略b下采样得到的样本序列:$\{ S_t,A_t,R_{t+1},...,S_{T-1},A_{T-1},R_T,S_T \}$,产生该样本序列的概率为$\prod_t^{T-1}{b\left( A_t|S_t \right)P\left( S_{t+1},R_{t+1}|S_t,A_t \right)}$。 在目标策略$\pi$下产生同样样本序列的概率为$\prod_t^{T-1}{\pi\left( A_t|S_t \right)P\left( S_{t+1},R_{t+1}|S_t,A_t \right)}$。 $\rho_{t:T-1}=\frac{\prod_t^{T-1}{\pi\left( A_t|S_t \right)P\left( S_{t+1},R_{t+1}|S_t,A_t \right)}}{\prod_t^{T-1}{b\left( A_t|S_t \right)P\left( S_{t+1},R_{t+1}|S_t,A_t \right)}}=\frac{\prod_t^{T-1}{\pi\left( A_t|S_t \right)}}{\prod_t^{T-1}{b\left( A_t|S_t \right)}}$,$\rho_{t:T-1}$即为重要性权重。 以每次访问型方法为例,$\tau\left( s,a \right)$表示(s,a)在每一幕中出现时刻的集合,$T\left( t \right),t\in \tau\left( s,a \right)$表示时刻t所在幕的终止时刻,两种采样方式如下所示: 普通重要性采样:$Q\left( s,a \right) =\frac{\sum_{t\in \tau \left( s,a \right)}{\rho _{t+1:T\left( t \right) -1}G_t}}{\left| \tau \left( s,a \right) \right|}$ 加权重要性采样:$Q\left( s,a \right) =\frac{\sum_{t\in \tau \left( s,a \right)}{\rho _{t+1:T\left( t \right) -1}G_t}}{\sum_{t\in \tau \left( s,a \right)}{\rho_{t+1:T\left( t \right)-1}}}$ 下面是离轨策略MC预测算法:
在遍历每一幕时,我们仍旧使用增量式的更新方法来计算加权平均: 加权平均增量式更新的推导过程: $c_{k}=\sum_{i}^{k}{w_{i}}\\\mu_{k}=\frac{\sum_{i}^{k}{w_{i}x_{i}}}{c_{k}}=\frac{\sum_{i}^{k-1}{w_{i}x_{i}}+w_{k}x_{k}}{c_{k}}=\frac{c_{k-1}\mu_{k-1}}{c_{k}}+\frac{w_{k}x_{k}}{c_{k}}=\frac{\left( c_{k}-w_{k} \right)\mu_{k-1}}{c_{k}}+\frac{w_{k}x_{k}}{c_{k}}=\mu_{k-1}+\frac{w_{k}}{c_{k}}\left( x_{k}-\mu_{k-1} \right)$ 下面是离轨策略MC控制算法:
二、蒙特卡洛实例 1、游戏背景介绍 请参考:https://www.cnblogs.com/lihanlihan/p/15956427.html 2、代码实现 (1)同轨策略的首次访问型MC控制算法 import numpy as np import gym from gym.spaces import Discrete from contextlib import contextmanager import time class SnakeEnv(gym.Env): #棋格数 SIZE = 100 def __init__(self, dices): #动作上限列表 self.dices = dices #梯子 self.ladders = {82: 52, 52: 92, 26: 66, 98: 22, 14: 22, 96: 63, 35: 12, 54: 78, 76: 57} #状态空间 self.observation_space = Discrete(self.SIZE + 1) #动作空间 self.action_space = Discrete(len(dices)) #初始位置 self.pos = 1 def reset(self): self.pos = 1 return self.pos def step(self, a): step = np.random.randint(1, self.dices[a] + 1) self.pos += step #到达终点,结束游戏 if self.pos == 100: return 100, 100, 1, {} #超过终点位置,回退 elif self.pos > 100: self.pos = 200 - self.pos if self.pos in self.ladders: self.pos = self.ladders[self.pos] return self.pos, -1, 0, {} def reward(self, s): if s == 100: return 100 else: return -1 def render(self): pass class TableAgent(): def __init__(self, env): #状态空间数 self.s_len = env.observation_space.n #动作空间数 self.a_len = env.action_space.n #训练时使用ε-贪心策略,测试时使用贪心策略 self.pi = np.full([self.s_len, self.a_len], 1 / self.a_len) #状态-动作价值函数 self.value_q = np.zeros((self.s_len, self.a_len)) #q(s,a)采样数 self.value_n = np.zeros((self.s_len, self.a_len)) #打折率 self.gamma = 0.5 def play(self, state): return np.random.choice(a = np.arange(self.a_len), p = self.pi[state]) class MonteCarlo(): def __init__(self): pass def monte_carlo(self, agent, env, epsilon): for i in range(20000): #采样 state = env.reset() episode = [] while True: ac = agent.play(state) next_state, reward, terminate, _ = env.step(ac) episode.append((state, ac, reward)) state = next_state if terminate: break #计算(s,a)的长期回报 value = [] return_val = 0 for item in reversed(episode): return_val = return_val * agent.gamma + item[2] value.append((item[0], item[1], return_val)) states = {} f = 0 for item in reversed(value): #first-visit if not states.get((item[0], item[1]), False): states[(item[0], item[1])] = True d = agent.value_q[item[0]][item[1]] agent.value_n[item[0]][item[1]] += 1 agent.value_q[item[0]][item[1]] += (item[2] - agent.value_q[item[0]][item[1]]) / agent.value_n[item[0]][item[1]] f = max(f, abs(agent.value_q[item[0]][item[1]] - d)) max_act = np.argmax(agent.value_q[item[0], :]) agent.pi[item[0]] = epsilon / agent.a_len agent.pi[item[0]][max_act] += 1 - epsilon print(f) def eval_game(env, policy): state = env.reset() return_val = 0 for epoch in range(100): while True: if isinstance(policy, TableAgent): act = policy.play(state) elif isinstance(policy, list): act = policy[state] else: raise IOError('Illegal policy') state, reward, terminate, _ = env.step(act) return_val += reward if terminate: break return return_val / 100 @contextmanager def timer(name): start = time.time() yield end = time.time() print('{} cost:{}'.format(name, end - start)) def monte_carlo_demo(): env = SnakeEnv([3, 6]) agent = TableAgent(env) mc = MonteCarlo() with timer('耗时'): mc.monte_carlo(agent, env, 0.2) policy = [] for i in range(agent.s_len): policy.append(np.argmax(agent.pi[i])) print('贪心策略:', policy) monte_carlo_demo()运行结果:
利用eval_game函数测试贪心策略结果:
(2)离轨策略MC控制算法 import numpy as np import gym from gym.spaces import Discrete from contextlib import contextmanager import time class SnakeEnv(gym.Env): #棋格数 SIZE = 100 def __init__(self, dices): #动作上限列表 self.dices = dices #梯子 self.ladders = {82: 52, 52: 92, 26: 66, 98: 22, 14: 22, 96: 63, 35: 12, 54: 78, 76: 57} #状态空间 self.observation_space = Discrete(self.SIZE + 1) #动作空间 self.action_space = Discrete(len(dices)) #初始位置 self.pos = 1 def reset(self): self.pos = 1 return self.pos def step(self, a): step = np.random.randint(1, self.dices[a] + 1) self.pos += step #到达终点,结束游戏 if self.pos == 100: return 100, 100, 1, {} #超过终点位置,回退 elif self.pos > 100: self.pos = 200 - self.pos if self.pos in self.ladders: self.pos = self.ladders[self.pos] return self.pos, -1, 0, {} def reward(self, s): if s == 100: return 100 else: return -1 def render(self): pass class TableAgent(): def __init__(self, env): #状态空间数 self.s_len = env.observation_space.n #动作空间数 self.a_len = env.action_space.n #目标策略 self.pi = np.zeros(self.s_len) #行动策略 self.b = np.full([self.s_len, self.a_len], 1 / self.a_len) #动作价值函数 self.value_q = np.zeros((self.s_len, self.a_len)) #(s,a)采样数 self.c = np.zeros((self.s_len, self.a_len)) #打折率 self.gamma = 0.5 def play(self, state): #训练时使用策略b,测试时使用策略π return np.random.choice(a = np.arange(self.a_len), p = self.b[state]) class MonteCarlo(): def __init__(self): pass def monte_carlo(self, agent, env, epsilon): for i in range(20000): #采样 state = env.reset() episode = [] while True: ac = agent.play(state) next_state, reward, terminate, _ = env.step(ac) episode.append((state, ac, reward)) state = next_state if terminate: break #计算(s,a)的长期回报 value = [] return_val = 0 for item in reversed(episode): return_val = return_val * agent.gamma + item[2] value.append((item[0], item[1], return_val)) f = 0 w = 1 #every-visit for item in value: d = agent.value_q[item[0]][item[1]] agent.c[item[0]][item[1]] += w agent.value_q[item[0]][item[1]] += (w / agent.c[item[0]][item[1]]) * (item[2] - agent.value_q[item[0]][item[1]]) f = max(f, abs(agent.value_q[item[0]][item[1]] - d)) max_act = np.argmax(agent.value_q[item[0]]) agent.pi[item[0]] = max_act if item[1] != agent.pi[item[0]]: break w *= 1 / agent.b[item[0]][item[1]] #b使用ε-贪心策略 for state in range(agent.s_len): max_act = np.argmax(agent.value_q[state]) agent.b[state] = epsilon / agent.a_len agent.b[state][max_act] += 1 - epsilon print(f) def eval_game(env, policy): state = env.reset() return_val = 0 for epoch in range(100): while True: if isinstance(policy, TableAgent): act = policy.play(state) elif isinstance(policy, list): act = policy[state] else: raise IOError('Illegal policy') state, reward, terminate, _ = env.step(act) return_val += reward if terminate: break return return_val / 100 @contextmanager def timer(name): start = time.time() yield end = time.time() print('{} cost:{}'.format(name, end - start)) def monte_carlo_demo(): env = SnakeEnv([3, 6]) agent = TableAgent(env) mc = MonteCarlo() with timer('耗时'): mc.monte_carlo(agent, env, 0.5) print('目标策略:', list(agent.pi.astype(np.int32))) monte_carlo_demo()运行结果:
利用eval_game函数测试目标策略结果:
|
【本文地址】