自考《离散数学》题型总结 |
您所在的位置:网站首页 › 自考税法知识点总结 › 自考《离散数学》题型总结 |
自考《离散数学》题型总结
|
第一章:命题与命题公式
(2道选择或填空,1道解答题,共8分左右)
1、选择、填空:
(1)命题符号化(每年第一题):
例:①:2021年10月: 1. 设 p:今年是 2020 年,q:明年是 2021 年,命题“只有今年是 2020 年,明年才是 2021 年的符 号化为 A. p∧q B. p∨q C. p→q D. q→p
解析:一般做这类题型搞清楚谁是谁的前提就可以,例如明年是2021年的前提是今年是2020年,所以例①选D。 (2)求一个公式的矛盾式或永真式例:2021年4月:
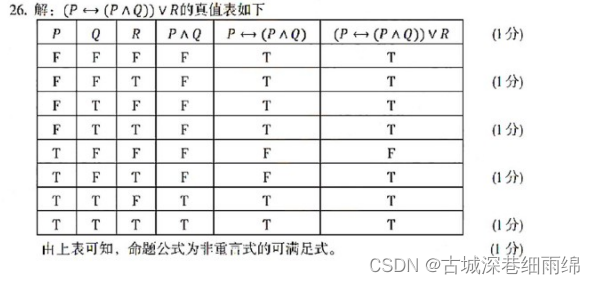
解析:一般做这类题型只需用等值演算法算出就可以,也可以用假设法设其中一个值为T或F,看整个公式能不能取真,如果能,则不是矛盾式,如果不管取T或F,公式都是F,则是矛盾式。实在不会也可以用真值表法,方法还是比较多的。 用等值演算法求得D最后得公式为:P∧¬Q∧Q,为矛盾式(永假式),所以选D。 ★(3)用真值表法求一个式子是否为可满足式(简答题第一题)例:
解析:这类题一般很好拿分,只要细心一点就没问题。
例:小赵、小钱、小孙、小李参加数学建模竞赛,根据下列情况,确定 4 人中获奖的是哪些人,未获奖的是哪 些人。需写出推导过程。 (1)只要小赵或小钱中一人未获奖,小孙和小李就都得奖; (2)小孙没获奖或小李没获奖是 不可能的; (3)小钱获奖了。 解析:做此类题首先把命题符号化再求他们的合取,用等值演算就可求出结果
2021年10月:
2021年4月:
解析:只需要记住小项打的的性质就可: 小项:每个小项当其真指派与编码相同时为T,其余都是F,所以任意两个小项的合取是永假,全体小项的析取为真,有2的n次方个小项。 大项:每个大项项当其真指派与编码相同时为F,其余都是T,所以任意两个大项的析取取是永真,全体小项的合取为假,有2的n次方个大项。 (2)求大小项的个数:2020年10月:
答案:1个 2020年8月: 答案:3个 解析:用等值演算法或者真值表法求就可以求出来,看清是求主合取还是主析取。以2020年10月为例:
2021年10月:
2021年4月: |
【本文地址】