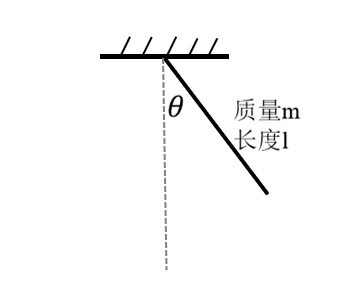
对于连续系统而言，最通用的方式是用一个微分方程来描述系统的特性： x ˙ = f ( x , u ) (1) \begin{align} \dot{x} &= f(x, u) \end{align}\tag{1} x˙​=f(x,u)​(1) 其中， x x x是系统的状态（state），u是系统的输入（input）。对于一个机器人系统来说， x x x通常定义成 x = [ q v ] (2) \begin{align} x &= \begin{bmatrix} q \\ v \end{bmatrix} \end{align}\tag{2} x​=[qv​]​(2) 其中， q q q是系统的configuration， v v v是系统速度。 q q q所张成的空间叫做configuration space，整个state space是由 q q q和 v v v一起构成的流形（manifold）。这个系统描述只有在smooth的时候才是成立的，在某些时候，如四足点着地了，则方程不成立。

ps：在课上教授提了一句， q q q并不一定是属于 R n \mathbb{R}^n Rn的，但是 v v v一定是。比如对于单摆系统来说， q q q是单摆的角度，是属于 − π -\pi −π到 π \pi π的，因此它所张成的空间是一个圆（因为对于单摆系统来说，转满 π \pi π之后则单摆会到的又是 − π -\pi −π的空间了，因此这是一个自己包着自己的compact manifold）。但是对于 v v v来说，它的范围是负无穷到正无穷，因此是属于实数空间的。两者一起构成的state space因此是一个圆柱流形。二阶倒立摆的configuration space是一个圆环流形（torus）。

对于如图1所示的单摆系统， m l 2 θ ¨ + m g l sin ⁡ ( θ ) = τ (3) \begin{align} m l^2 \ddot{\theta} + m g l \sin(\theta) = \tau \end{align}\tag{3} ml2θ¨+mglsin(θ)=τ​(3) 其中， l l l是单摆的长度， θ \theta θ是单摆的角度， τ \tau τ是输入的力矩。通过变换可以得出如下方程 x ˙ = [ θ ˙ θ ¨ ] = [ θ ˙ − g l sin ⁡ θ + 1 m l 2 u ] = f ( x , u ) (4) \begin{align} \dot{x} &= \begin{bmatrix} \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{\theta} \\ -\frac{g}{l} \sin{\theta} + \frac{1}{m l^2} u \end{bmatrix} = f(x,u) \end{align}\tag{4} x˙​=[θ˙θ¨​]=[θ˙−lg​sinθ+ml21​u​]=f(x,u)​(4)

许多系统，特别是机电系统（mechanical systems）都可以写成如下形式 x ˙ = f 0 ( x ) + G ( x ) u (5) \begin{align} \dot{x} = f_{0} (x) + G(x) u \end{align}\tag{5} x˙=f0​(x)+G(x)u​(5) 这是连续性系统方程的一种特殊的形式，控制输入通过仿射矩阵 G G G来直接作用于系统。对于单摆系统来说， f 0 ( x ) = [ θ ˙ − g l sin ⁡ ( θ ) ]     G ( x ) = [ 0 1 m l 2 ] (6) \begin{align} f_{0}(x) = \begin{bmatrix} \dot{\theta} \\ - \frac{g}{l} \sin(\theta) \end{bmatrix} \ \ \ G(x) = \begin{bmatrix} 0 \\ \frac{1}{ml^2} \end{bmatrix} \end{align}\tag{6} f0​(x)=[θ˙−lg​sin(θ)​]   G(x)=[0ml21​​]​(6)

ps：课上教授提到，如果系统存在一些u和x的复杂耦合关系使系统无法写成这种标准形式，仍然可以通过一些数学上的trick，通过引入新的状态 x x x，这个x中包含有原本的 x x x和 u u u中的耦合部分，则可以变换成这种控制仿射系统。

搞机械臂相关的同学肯定不会陌生下面这种形式的系统方程（可以有许多种表达式，但都是等价的）。 M ( q ) v ˙ + C ( q , u ) = B ( q ) u (7) \begin{align} M(q) \dot{v} + C(q,u) = B(q) u \end{align}\tag{7} M(q)v˙+C(q,u)=B(q)u​(7) 其中， M ( q ) M(q) M(q) 是系统的质量矩阵, C ( q , u ) C(q,u) C(q,u) 是dynamics bias (科氏力和重力)， B ( q ) B(q) B(q) 是输入矩阵， q q q 是configuration， v v v 是速度。 v v v不一定是 q q q的导数，它们可能存在如下关系 q ˙ = G ( q ) v (8) \begin{align} \dot{q} = G(q) v \end{align}\\\tag{8} q˙​=G(q)v​​(8) 对于上述单摆系统， M ( q ) = m l 2 M(q) = ml^2 M(q)=ml2, C ( q , u ) = q l sin ⁡ ( θ ) C(q,u) = q l \sin(\theta) C(q,u)=qlsin(θ), B = I B=I B=I, G = I G=I G=I。

ps：课上教授说，所有的机电系统都可以描述成这种形式，因为这是牛顿-欧拉方程的特殊表达方式而已。还不太理解。

线性系统具有如下形式 x ˙ = A ( t ) x + B ( t ) u (9) \begin{align} \dot{x} = A(t) x + B(t) u \end{align}\tag{9} x˙=A(t)x+B(t)u​(9) 由于线性系统控制理论相较来说已经比较成熟了，因此我们通常将一个具有通用形式的(1)系统在当前状态处线性化，则有 A = ∂ f ∂ x A = \frac{\partial f}{\partial x} A=∂x∂f​ and B = ∂ f ∂ u B = \frac{\partial f} {\partial u} B=∂u∂f​。

平衡点的定义是，系统状态的变化量为0，因此如果系统处于该状态，那么将一直保持于此。 x ˙ = f ( x , u ) = 0 (10) \begin{align} \dot{x} = f(x,u) = 0 \end{align}\tag{10} x˙=f(x,u)=0​(10) 代数上这就是一个求根的问题。我们将单摆系统的状态方程带入（在输入 u u u为0时）， x ˙ = [ θ ˙ − g l sin ⁡ ( θ ) ] = [ 0 0 ] (11) \begin{align} \dot{x} = \begin{bmatrix} \dot{\theta} \\ -\frac{g}{l} \sin(\theta) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \end{align}\tag{11} x˙=[θ˙−lg​sin(θ)​]=[00​]​(11) 可以得到在 θ = 0 , π \theta=0,\pi θ=0,π 和 θ ˙ = 0 \dot{\theta}=0 θ˙=0时是系统的平衡点。

ps：通过提供系统输入u，可以改变系统平衡点，如我们令 u = m g l u=mgl u=mgl，则系统的平衡点会变到 π / 2 \pi/2 π/2。注意这个u只是说，当系统状态处于那个点时，我们提供这种输入可以让系统状态在该点平衡，而不是说，我只要一直提供这种u，就可以把系统状态转移到这个平衡点。

一个稳定的平衡点，在该点处受到微小的扰动后，应该是能够重新回到该平衡点的，考虑一维下的情况，一个3次多项式的系统方程。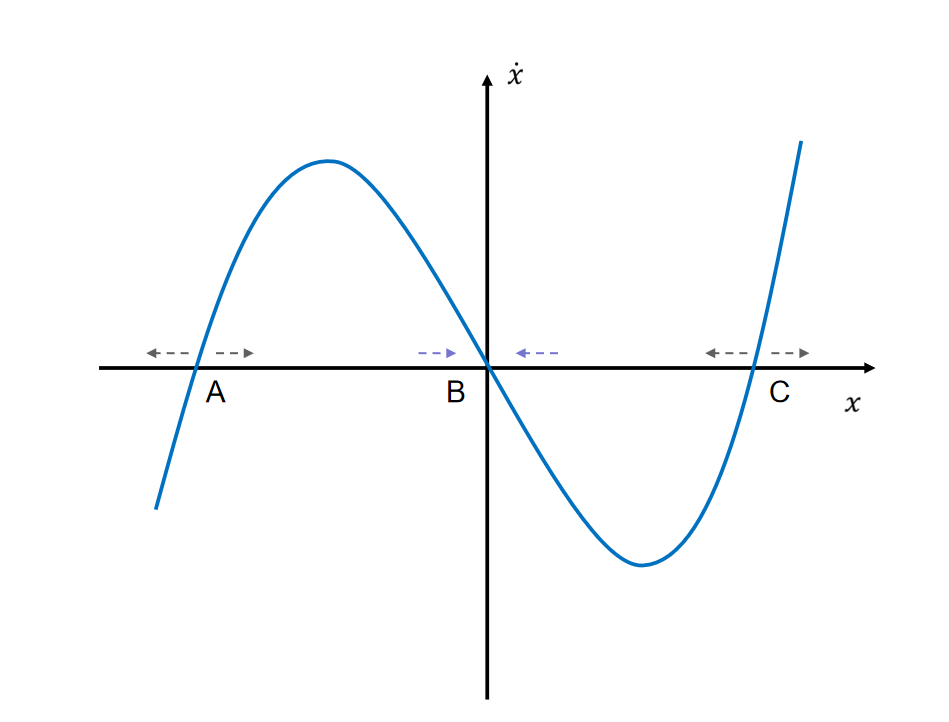

可以看出，从左到右系统有 A   B   C A\ B\ C A B C三个平衡点，在B点时，若我们将其扰动到相平面右边，从曲线中可以看出，此时系统的 x ˙ \dot{x} x˙是负的，因此此时 x x x会变小，则会回到相平面的原点。反观 A   C A \ C A C点，当我们向右扰动时， x ˙ \dot{x} x˙为正， x x x就有了继续往右走的趋势，因此无法回到平衡点，这两个平衡点即是不稳定的。

进一步地，我们可以总结，当平衡点处 ∂ f ∂ x < 0 \frac{\partial f}{\partial x}