树状数组(BIT) |
您所在的位置:网站首页 › 结构体bit定义及应用 › 树状数组(BIT) |
树状数组(BIT)
|
目录树状数组(BIT)—— 一篇就够了前言、内容梗概什么是 BIT ?起源与介绍BIT 的原理BIT 的询问,更新操作及其代码实现queryupdate模板BIT 的优缺点,比较与应用场景优缺点应用场景与比较树状数组的经典例题及其技巧模板题:单点修改,区间查询思路:代码:模板题:区间修改,区间查询思路:代码逆序对 简单版思路代码一代码二逆序对加强版: 翻转对思路代码二维BIT:区间查询,单点修改思路代码后记
树状数组(BIT)—— 一篇就够了
前言、内容梗概
本文旨在讲解: 树状数组的原理(起源,原理,模板代码与需要注意的一些知识点) 树状数组的优势,缺点,与比较(eg:线段树) 树状数组的经典例题及其技巧(普通离散化,二分查找离散化) 什么是 BIT ? 起源与介绍树状数组或二元索引树(英语:Binary Indexed Tree),又以其发明者命名为 \(\mathrm{Fenwick}\) 树。最早由 \(\mathrm{Peter\; M. Fenwick}\) 于1994年以 《A New Data Structure for Cumulative Frequency Tables[1]》为题发表在 《SOFTWARE PRACTICE AND EXPERIENCE》。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。它可以以 \(\mathcal{O(\log n)}\) 的时间得到任意前缀和(区间和)。 很多初学者肯定和我一样,只知晓 BIT 代码精炼,语法简明。对于原理好像了解,却又如雾里探花总感觉隔着些什么。 按照 Peter M. Fenwick 的说法,BIT 的产生源自整数与二进制的类比。 Each integer can be represented as sum of powers of two. In the same way, cumulative frequency can be represented as sum of sets of subfrequencies. In our case, each set contains some successive number of non-overlapping frequencies. 简单翻一下:每个整数可以用二进制来进行表示,在某些情况下,序列累和(这里没有翻译为频率)也可以用一组子序列累和来表示。在本例子中,每个集合都有一些连续不重叠的子序列构成。 实际上, BIT 也是采用类似的想法,将序列累和类比为整数的二进制拆分,每个前缀和拆分为多个不重叠序列和,再利用二进制的方法进行表示。这与 Integer 的位运算非常相似。 之所以命名为: Binary Indexed Tree,在论文中 Fenwick 有如下解释: In recognition of the close relationship between the tree traversal algorithms and the binary representation of an element index,the name "binar indexed tree" is proposed for the new structure. 也就是考虑到:树的遍历方法与二值表示之间的紧密联系,因此将其命名为二元索引树。 BIT 的原理在介绍原理之前先对于一些关键的符号做出定义: \[\begin{array} x\hline 符号 & 解释 \\ \hline f[i] & 原数组第 i 位的值 \\ tree[i] & \mathrm{BIT}中定义的子序列和数组,tree[i]代表某一序列的和\\ c[i] & 代表 \sum_{k=1}^{k=i} f[i], 即前缀和\\ \hline \end{array} \]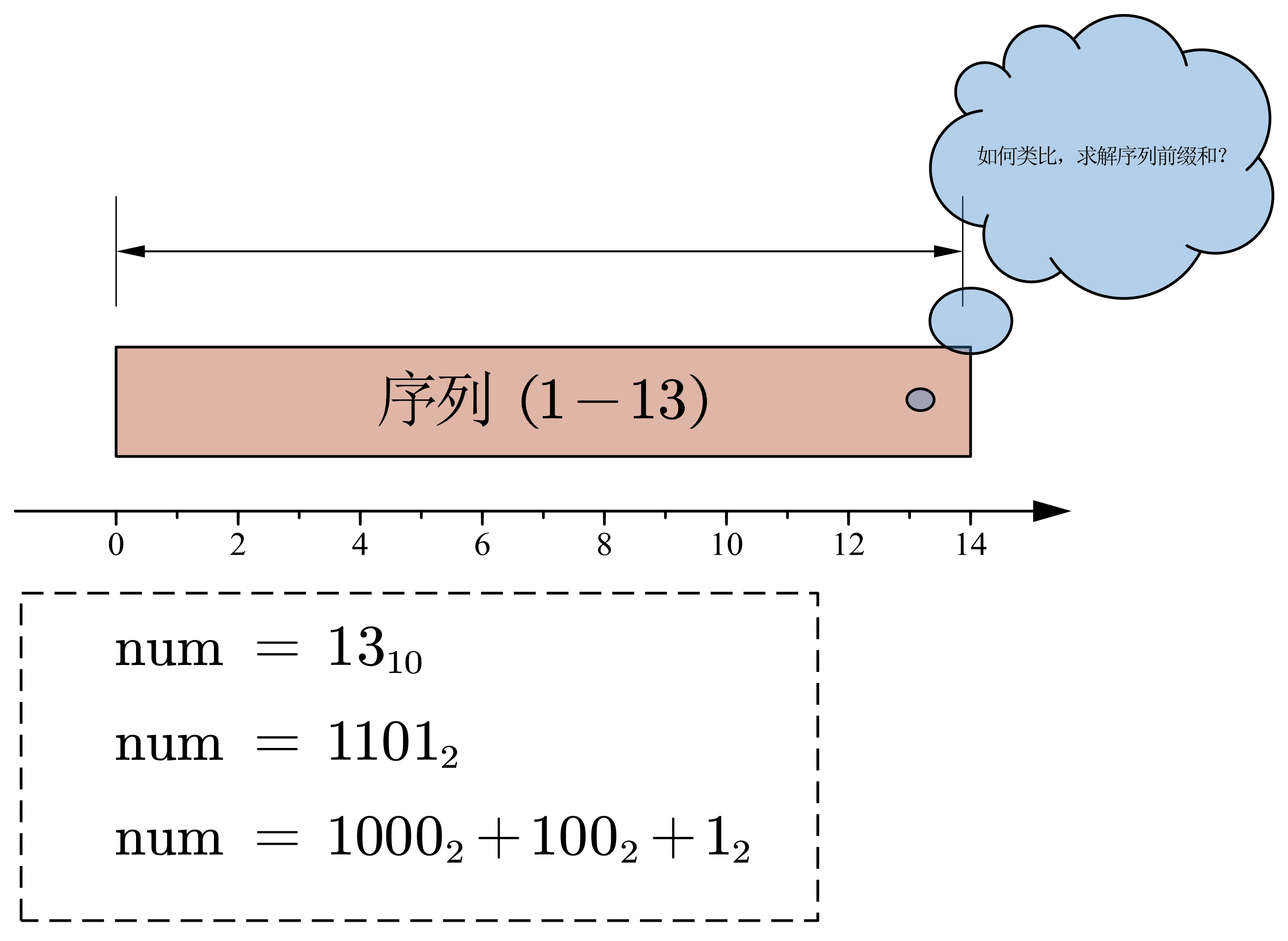 第一步:思考整数二进制拆分与序列前缀和的类比
第一步:思考整数二进制拆分与序列前缀和的类比
在学习 BIT 时,很容易忽略 BIT 设计的思想,而仅仅停留在对于其代码简洁精炼的赞叹上,所以第一步我们将体会 BIT 是如何类比;如何设计;如何实现的。 如上图所示:我们给定一个整数: \(num = 13\) 我们尝试将 \(num\) 用二进制进行表示: \(1101_2 = 1000_2 + 100_2 + 1_2\) 。可以看到 \(num\) 可以由\(3\)个二进制数组成。且拆分的个数总是 \(\mathcal{O(\log_2n)}\) 级的,因此我猜想Fenwick便开始思考如何将一个子序列,借助二进制的特点快速的表示出来。 
首先,依据最简单的拆分方法(即与二进制拆分相同)如图左示。显然这个方法具有缺陷,某些序列会被重复计算,而有些序列则没有被包含在内,因此解决问题的关键,同时也是 BIT 的核心思想便是如何基于编号,构件一个不重叠的子序列集合。 如右图所示,该拆分方案能很好的实现不重叠的子序列集合,我们尝试将其列出以发现其中的规律: \[\begin{aligned} &num = 13 =1101_2 \\ &子序列_1 = f[1](f[0001_2]) + f[2] +\cdots + f[8](f[1000_2]) \quad len(1000_2)\\ &子序列_2 = f[9](f[1001_2]) + f[10]+\cdots + f[12](f[1100_2]) \quad len(0100_2)\\ &子序列_3 = f[13](f[1101_2]) \quad len(0001_2) \end{aligned} \]经过观察: \(子序列_1\) 表示的范围在 \([0001_1, 1000_2] \rightarrow [0000_2 + 1, 0000_2 + 1000_2]\)。 \(子序列_2\) 的表示范围在 \([1001_2, 1100_2] \rightarrow [1000_2 + 1, 1000_2 + 0100_2]\)。 \(子序列_3\) 的表示范围在 \([1101_2, 1101_2] \rightarrow [1100_2 + 1, 1100_2 + 0001_2]\)。设某编号的二进制为 \(\mathrm{XXX}bit\mathrm{XXX}_2\) ,设 \(bit\) 为当前需要考虑的位\((bit=1)\),\(\mathrm{X}\) 为\(0 \;or\; 1\) ,则其表示的范围是: \([XXX0000_2 + 1, XXX0000_2 + bit000_2]\) ,换一句话说:假如序列编号在 \(bit\) 位为1,则其代表的子序列具有如下性质: 子序列的基准量为:\(base = 将二进制编号中bit及其之后所有位置0代表的值\quad eg: num=1101_2,bit=第3位(1-index), 则base = 1000_2\) 子序列的偏移量:\(offset=1 f[i]; BIT bit(f, n); for (int i = 0; i < q; ++ i){ int type; cin >> type; if (type == 1){ int i, x; cin >> i >> x; bit.add(i, (ll) x); }else { int l, r; cin >> l >> r; cout > q; BIT bit1, bit2; for (int i = 1; i > f[i]; bit1.init(n), bit2.init(f, n); for (int i = 0; i < q; ++ i){ int type; cin >> type; if (type == 1){ int l, r, x; cin >> l >> r >> x; bit2.add(l, (ll) -1 * (l - 1) * x), bit2.add(r + 1, (ll) r * x); bit1.add(l, (ll) x), bit1.add(r + 1, (ll) -1 * x); }else { int i; cin >> i; cout ans = 0 BIT: 0, 1, 0, 0 >1, sum(1) = 0, ans += 1 - sum(1) -> ans = 1 BIT: 1, 1, 0, 0 >3, sum(3) = 2, ans += 2 - sum(3) -> ans = 1 BIT: 1, 1, 1, 0 >4, sum(4) = 3, ans += 3 - sum(4) -> ans = 1实际上,便是借助 BIT 高效计算前缀和的性质实现了快速打标记,先统计在我之前有多少个标记(这些都是合法对),再将自己所在位置的标记加 \(1\)。 因此,很容易写出这段代码: 代码一 // 仅保留核心代码 int reversePairs(vector& nums) { int n = nums.size(); if (n == 0) return 0; int mx = *max_element(nums.begin(), nums.end()); BIT bit(mx); // 因为最大只到最大值的位置 int ans(0); for (int i = 0; i < n; ++ i){ ans += (i - bit.sum(nums[i])); bit.add(nums[i], 1); } return ans; }但是这个代码有非常严重的问题,首先假如 mx = 1e9 就会出现段错误;或者假如 nums[i] < 0 则会出现访问越界的问题,但是实际上题目中说明了:数组最多只有 50000个元素,也就是我们需要想办法将坐标离散化,保留其大小顺序即可。 代码二 #define lb lower_bound #define all(x) x.begin(), x.end() const int maxn = 5e4 + 50; struct node{ int v, id; }f[maxn]; // 离散化结构体 int arr[maxn]; bool cmp(const node&a, const node &b){ return a.v < b.v; } class Solution { public: int reversePairs(vector& nums) { int n = nums.size(); if (n == 0) return 0; BIT bit(n); for (int i = 1; i |
【本文地址】