连续体结构拓扑优化方法介绍 |
您所在的位置:网站首页 › 结构优化步骤 › 连续体结构拓扑优化方法介绍 |
连续体结构拓扑优化方法介绍
|
连续体结构拓扑优化方法介绍
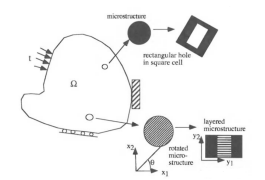
材料的有效利用一直是人类追求的目标,也是许多研究领域不变的话题,并伴随着结构优化理论和方法的产生而发展。早期结构优化主要是针对尺寸的优化问题,设计域形状是固定的。后来随着结构优化问题的提出,形状优化方法[1]应运而生。在航空和汽车制造行业,经常应用尺寸和形状优化技术设计结构和零件,形状优化方法也常被用来进行电磁、电化学和声学零件的设计,目前已经有许多成功的算法可以处理这类非线性和有限维的问题[2,3]。 形状优化方法是以边界变分为基础,在结构设计中仍占有重要的位置,设计变量直接控制着结构内外边界的形状。但是其主要的缺点是最终设计结果的拓扑与初始给定的拓扑相同,即便如此,在优化过程中还需要多次重新划分有限元网格,如要在设计过程中改变结构的拓扑,则将使设计问题更加复杂[1]。 为了更有效利用材料,弥补形状优化固定拓扑的局限性,拓扑优化问题被提了出来,对于一个新的设计问题,在优化过程中它要求能够产生新的孔,其拓扑和形状没有先验信息给出,优化算法必须在所谓的参考域内确定材料的最优分布,这种分布能极小化给定的目标函数,并满足强加的约束,因此,拓扑优化问题可以被看作是材料的分配问题,需要确定参考域中每一点材料的特征。由于它的复杂性,拓扑优化是结构优化中更具挑战性的研究课题。 连续体结构拓扑优化的重要发展源于1981年Cheng和Olhoff[4,5]的工作,他们在研究最大刚度变厚板最优设计时,发现最优解中包含许多各种尺寸的加强筋,具有非光滑的特征,这意味着最优设计中必须引入复合材料,拓展最优设计空间。这导致了随后一系列研究进展,包括1984年Lurie等[6]用G-收敛理论解释拓扑优化过程中的非光滑现象;Kohn和Strang等[7]引入松弛概念来处理拓扑优化中的病态变分问题,并论证了这种松弛和均匀化之间的关系;Murat和Tartar[8]引入了特征函数来处理拓扑优化的问题,并指出用均匀化进行松弛处理的必要性;Rozvany等[9]研究了在设计加强筋板中引进松弛的含义。这些研究工作直接导致了1988年Bendsoe和Kikuchi[10]提出了连续体结构拓扑优化的均匀化方法,标志着连续体拓扑优化进入蓬勃发展的阶段。 自从均匀化方法被提出以来,在过去的近三十年中,又有多种连续体结构拓扑优化方法被提出,如“带惩罚指数的固体各向同性微结构模型”(SIMP: Solid Isotropic Microstructures with Penalization)方法[11,12]、结构进化法(ESO)[13,14]、冒泡法(Bubble Method)[15]以及水平集方法(Level Set Method)[16,17]等各种各样的方法。这些方法已经在工程技术领域有着广泛的应用。 1)均匀化方法 均匀化方法的数学理论是20世纪70年代在预测与复合材料等效的均匀化材料的宏观特性时提出来的,其在许多工程领域都有应用,如:多孔介质的流体流动、复合材料中的电磁场等[18]。在均匀化方法中,借助周期微结构的复合材料,将拓扑优化问题转化为复合材料微结构的参数的尺寸设计问题,应用一定的最优化准则或者数学规划法来寻找多孔介质的最优配置。微结构的引入,解决了原来拓扑优化中材料分配中只能在离散集合{0,1}上取值的问题,使其可以在区间[01]上取值,这种设计空间的拓展,保证了拓扑优化最优解的存在。在Bendsøe和Kikuchi[10]1988年首次将均匀化方法成功用于连续体结构的拓扑优化设计中,建立了以结构柔度最小为目标函数,结构体积为约束的连续体结构的拓扑优化设计模型,均匀化方法得到广泛的应用。Suzuki和Kikuchi[19],Guedes和Kikuchi[20],Hassani和Hinton[21],Fernandes等[22]对此方法进行不断完善和发展,并由Diaz和KiKuchi[23]和Ma等[24]进一步推广至特征频率问题的结构拓扑优化,Nishiwaki等[25]将均匀化理论应用于柔性机构的拓扑优化设计中。但这种方法也存在其不足,在优化过程中需要确定微结构和微结构的方向,这样有时显得过于繁琐,同时优化结果中常包含多孔介质材料,也难以制造。同时,因为设计变量多,敏度计算复杂,使得优化求解效率也不高。
[3]Michell A G M. The limit of economy of material in framestructures. Philosophical Magazine, 1904, 8 (6): 589~597 [4]Cheng Gd, Olhoff N. An investigationconcerning optimal design of solid elastic plates. International Journal ofsolids and structures, 1981,17: 305~323 [5]Cheng Gd, Olhoff N. Regularizedformulation for optimal design of axisymmetric plates. International Journal ofsolids and structures, 1982, 18: 153~170 [6]Lurie K A , Cherkaev A V , Fedorov AV. On the existence of solution to some problems of optimal design for bars andplates. Journal of optimization theory and applications, 1984, 42(9): 247~281 [7]Kohn R V, Strang G. Optimal designand relaxation of variational problems. Communication in pure and applicationmathematics, 1986, Part I, 39:1~25, Part II, 39: 139~182, Part III, 39: 353~377 [8]Murat F, Tartar L. Optimalityconditions and homogenization. Nonlinear variational problems, Pitmanpublishing program, Boston, 1985 [9]Rozvany G I N, Ong T G, Seto W T.Least-weight design of perforated elastic plates. International Journal ofsolids and structures, 1987, Part I, 23: 521~536, Part II, 23: 537~550 [10]Bendsoe M P, Kikuchi N. Generatingoptimal topologies in structural design using a homogenization method. Computermethods in applied mechanics and engineering, 1988,71: 197~24 [11]Sigmund O. A 99 topologyoptimization code written in Matlab. Structural and multidisciplinaryoptimization, 2001, 21: 120~718 [12]Bendsøe M P, Sigmund O. Topology optimization:Theory, Methods, and Applications.Springer, New York, 2003 [13] Xie Y M, Steven G P. A simple evolutionaryprocedure for structural optimization. Computers & Structures, 1993, 49(5): 885~896 [14] Xie Y M, Steven G P. Evolutionarystructural optimization. Springer, 1997 [15] Eschenauer H A, Kobelev H A,Schumacher A. Bubble method for topology and shape optimization of structures.Structural optimization, 1994, 8: 142~151 [16] Michael Y W, Xiaoming Wang, Dongming Guo. Alevel set for structural topology optimization. Computer Methods in AppliedMechanics and Engineering, 2003, 192: 227~246 [17] Allaire G, Jouve F, ToaderA M. Structural optimization using sensitivity analysis and a level-set method.Journal of Computational Physics, 2004, 194: 363~393. [18] Hassani B, Hilton E, A review ofhomogenization and topology optimization I-homogenization theory for media withperiodic. Computers and structures,1998, 69: 707~717 [19]Suzuki K, Kikuchi N. Ahomogenization method for shape and topology optimization. Computer methods inapplied mechanics and engineering, 1991, 93: 291~318 [20]Guedes J M, Kikuchi N. Preprocessing and Postprocessing for Materials Based on the Homogenization Method with AdaptiveFinite Element Method. Computer Methods in Applied Mechanics and Engineering,1990, 83: 143~198 [21]Hassani B, Hinton E. Homogenization andStructural Topology Optimization Theory, practice and Software. Springer, London, 1999 [22]Fernandes P, Guedes J M, Rodrigues H. TopologyOptimization of Three-Dimensional linear Elastic Structure with a Constraint on“perimeter”. Computer Methods in Applied Mechanics and Engineering, 1999, 73:583~594 [23]Diaz A, Kikuchi N. Solutions to shape andtopology eigenvalue optimization problem using a homogenization method.International Journal for Numerical Methods in Engineering, 1992, 35: 1487~1502 [24]Ma Z D, Kikuchi N, Cheng H C. Topological designfor vibrating structures. Computational Methods in Applied Mechanics andEngineering, 1995, 121: 259~280 [25]Nishiwaki S, Frecker M I, Min S, Kikichi N.Topology optimization of compliant mechanisms using the homogenization method.International Journal for Numerical Methods in Engineering, 1998, 42: 535~559 [26]Bendsoe M P, Sigmund O. Materialinterpolations in topology optimization. Archive of applied mechanics, 1999, 69:635~654 [27]Sigmund O, Pertersson J. Numericalinstabilities in topology optimization: A survey on procedures dealing withcheckerboards, mesh-dependencies and local minima. Structure optimization,1998, 16: 68~75, [28] Eschenauer H A, Olhoff N. Topologyoptimization of continuum structures: a review. Applied mechanics reviews,2001, 54, 4: 331~390 [29]QuerinO., Steven G., Xie Y., Evolutionary structural optimization (ESO) using abi-directional algorithm. Engineering Computations. 1998, 15(8): 1031-1048 [30]孙圣权, 张大可, 徐云岳等, 基于应力突变率的双向进化结构优化方法. 机械设计与研究. 2008, 24(2): 6-9 [31] AnsolaR., Vegueria E., Canales J., 3D compliant mechanisms synthesis by a finiteelement addition procedure. Finite Elements in Analysis and Design. 2010,46(9): 760-769 [32]LiQ., Steven G.P., Querin O.M., Shape and topology design for heat conduction byEvolutionary Structural Optimization. International Journal of Heat and MassTransfer. 1999, 42(17): 3361-3371 [33]XieY.M., Steven G.P., Evolutionary structural optimization for dynamic problems.Computers & Structures. 1996, 58(6): 1067-1073 [34]顾松年, 徐斌, 荣见华等, 结构动力学设计优化方法的新进展. 机械强度. 2005, 27(2): 156-162 [35]Osher S J, Sethian J A. Frontspropagating with curvature dependent speed: Algorithms based on theHamilton-Jacobi formulation. Journal of computational physics, 1988, 79: 12~49 [36]Sethian J A, Wiegmann A. Structuralboundary design via level set and immersed interface methods. Journal ofcomputational physics, 2000, 163(2): 489~528 [37]Wang M Y, Wang X M. ‘Color’level sets: a multiphase method for structural topology optimization withmultiple materials. Computer Methods in Applied Mechanics and Engineering,2004, 193: 469~496 [38]Wang M Y, Chen S K, Wang XM. Design of multi-material compliant mechanisms using level set methods.Journal of Mechanical Design, 2005, 127: 941~956 [39]Allaire G, Jouve F. A level-setmethod for vibration and multiple loads structural optimization. ComputerMethods in Applied Mechanics and Engineering, 2005, 194(30-33): 3269~3290 [40]Belytschko T, Xiao S P,Parimi C. Topology optimization with implicitly function and regularization.International Journal for Numerical Methods in Engineering, 2003, 57: 1177~1196 [41]Haber E. A multilevel,level-set method for optimizing eigenvalues in shape design problems. Journalof Computational Physics, 2004, 198: 518~534 [42]Amstutz S, Andra H. A newalgorithm for topology optimization using a level-set method. Journal ofComputational Physics, 2006, 216: 573~588 [43]Xia Q, Wang M Y, Wang S Y.Semi-Lagrange method for level-set structural topology and shape optimization.Structural and Multidisciplinary Optimization, 2006, 31: 419~429 [44]Chen J Q, Shapiro V, SureshK. Shape optimization with topological changes and parametric control.International Journal for Numerical Methods in Engineering, 2007, 71: 313~346 [45]Wang S Y, Wang M Y. Radial basis functions and level set methodfor structural topology optimization. International Journal for NumericalMethods in Engineering, 2006, 65: 2060~2090 [46]Luo Z, Wang M Y, Wang S Y.A level set-based parameterization method for structural shape and topologyoptimization. International Journal for Numerical Methods in Engineering, 2008,76(1): 1~26 [47] Wei P, Wang M Y. Apiecewise constant level set method for structural shape and topologyoptimization. in 7th World Congress of Structural and MultidisciplinaryOptimization, Seoul,Korea, 2007 |
【本文地址】
 2)SIMP方法 为提高均匀化方法的优化效率,许多学者纷纷致力于对均匀化方法的改进,其中最具代表性的就是固体各向同性材料惩罚法(SIMP),简称密度惩罚法[11,12]。由于该种方法容易现,计算效率高,已经成为最重要的拓扑优化方法,著名的拓扑优化软件Hyperworks.Optistruct就是采用该种方法。该种方法的基本思想就是假定单元的密度和材料物理属性(如:许用应力、弹性模量)之间的某种对应关系,以连续变量的密度函数形式显式地表达这种对应关系。变密度法基于各向同性材料,不需引入微结构、不需均匀化过程,它以每个单元的相对密度作为设计变量,每个单元有唯一的设计变量。这种做法一度受到质疑,因为没有相应的物理材料满足材料特性是其密度的幂函数。而Bendsoe和Sigmund[26]证明了其物理意义。为保证解的存在性,在算法实施时密度惩罚通常和边界结构长度约束、密度总变分约束或滤波技术结合[27]。其和均匀化方法的差别在于密度惩罚法接受中间密度值作为优化的工具,而均匀化方法接受中间密度值作为有效的设计特征,可以用微结构实现[28]。目前密度惩罚法已经被广泛应用于多约束、多物理场、多材料问题的拓扑优化设计。
2)SIMP方法 为提高均匀化方法的优化效率,许多学者纷纷致力于对均匀化方法的改进,其中最具代表性的就是固体各向同性材料惩罚法(SIMP),简称密度惩罚法[11,12]。由于该种方法容易现,计算效率高,已经成为最重要的拓扑优化方法,著名的拓扑优化软件Hyperworks.Optistruct就是采用该种方法。该种方法的基本思想就是假定单元的密度和材料物理属性(如:许用应力、弹性模量)之间的某种对应关系,以连续变量的密度函数形式显式地表达这种对应关系。变密度法基于各向同性材料,不需引入微结构、不需均匀化过程,它以每个单元的相对密度作为设计变量,每个单元有唯一的设计变量。这种做法一度受到质疑,因为没有相应的物理材料满足材料特性是其密度的幂函数。而Bendsoe和Sigmund[26]证明了其物理意义。为保证解的存在性,在算法实施时密度惩罚通常和边界结构长度约束、密度总变分约束或滤波技术结合[27]。其和均匀化方法的差别在于密度惩罚法接受中间密度值作为优化的工具,而均匀化方法接受中间密度值作为有效的设计特征,可以用微结构实现[28]。目前密度惩罚法已经被广泛应用于多约束、多物理场、多材料问题的拓扑优化设计。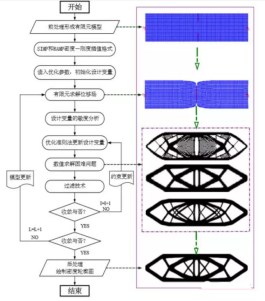 3)ESO方法 ESO方法由Xie和Steven[13]在1993年提出,是近年来兴起的一种基于进化策略的优化方法。该方法采用有限元法对设计空间进行离散化处理,离散网格所对应的单元作为设计变量,并采用“零”和“非零”对其进行编码,在位移、应力、频率、临界压力和刚度的约束下,通过设计合适的准则评估单元对目标函数变化的贡献值,并以此为依据对材料单元进行增删,从而逐渐逼近最佳的结构布局形式。相较于SIMP方法,ESO法能够获得清晰的0-1材料分布。最初的ESO方法亦可称为“硬杀法”(Hard Kill),即直接删除应变能密度最低的单元。随后,该方法被进一步改进为双向进化结构优化法(BESO: Bi-directional EvolutionaryStructural Optimization)[29,30],按照设定的规则删除和复活单元,实现结构拓扑的变化。尽管最初的ESO方法多依赖于直觉性,但随着研究的深入,类似于变密度法中的共轭梯度分析法和过滤技术也逐步被引入[31],以增强算法和优化结果的稳定性。ESO方法符合工程直观性,应用简单方便,目前已被成功用于解决不同类型的拓扑优化问题[32-34]。 4) 水平集方法 均匀化方法、SIMP方法以及进化结构法都是属于基于材料分布的拓扑优化方法,而冒泡法则属于基于几何边界的拓扑优化方法。基于几何边界的拓扑优化方法分为两类:隐式边界描述方法和显式边界描述方法,冒泡法属于典型的显式边界描述方法,而水平集方法则属于典型的隐式边界描述方法,同显式边界描述方法相比,隐式边界描述具有很多优点,如:不需要重新划分网格,能够同时描述结构的拓扑和形状变化等。 水平集方法是Osher和Sethian[35]1988年在研究曲线(或曲面)以曲率相关的速度演化时候提出来的,是描述曲线(或曲面)演化过程的一种方法。其主要思想就是引入水平集函数,将移动界面作为的零等值面嵌入到高一维的水平集函数中。在演化过程中,演化曲线(或曲面)总是对应于该零等值线(或面),只要确定零等值线(或面)即可确定移动界面的位置。 由于水平集方法在模型描述方面有许多优点,2000年Sethian和Wiegmann[36]首先将水平集方法引入到结构拓扑优化领域中,用来进行等应力结构的设计,发展了一种高边界分辨率的刚性结构拓扑优化方法。Wang等[16,37,38]扩展了水平集拓扑形状优化的方法,将水平集方法和形状导数结合起来,通过结构边界的法向速度建立了Hamilton-Jacobi偏微分方程同形状导数之间的关系,采用逆风策略来求解水平集方程,实现结构边界的演化直至获得最优解。Allaire等[17,39]提出了一种相似的水平集拓扑形状优化方法,其边界速度场是从严格的形状敏度分析中推导出来的,边界的演化通过Hamilton-Jacobi方程来实现,其后又将该方法应用到结构特征频率问题拓扑优化以及柔性机构拓扑优化等方面。 为了提高水平集方法的优化收敛速度,提高效率,减少因为逆风差分格式中CFL条件的限制而增加的计算消耗,几种改进的水平集方法被提了出来,例如:Belytschko等[40]提出了规则化隐函数的水平集拓扑形状优化方法,其通过优化策略直接更新一个窄带上的水平集函数的结点值来实现边界演化。Haber等[41]将序列二次规划法和多级网格细化法结合提出了一种改进的水平集方法来进行结构特征频率形状优化。Amstutz和Andra[42]提出一种拓扑导数概念的水平集方法拓扑优化方法。Xia等[43]提出了一种半拉格朗日的水平集方法,摆脱步长限制,很好地提高了优化效率,但该方法稳定性比较差。Chen等[44]将R函数和B样条曲线函数结合提出一种隐式边界描述的具有参数控制和拓扑变化的形状优化方法。Wang S Y等[45]将径向基函数引入到水平集方法中,用参数化的径向基函数代替原来的离散水平集函数描述方法,将原来水平集优化方法中的Hamilton-Jacobi偏微分方程转换成了常微分方程,摆脱了CFL条件的步长限制,有效提高了求解效率。Luo Z等[46]在径向基函数方法的基础上采用紧支径向基函数(CS-RBF)建立了一种参数化的水平集方法,以插值函数扩展系数作为设计变量,并采用最优化准则法更新设计变量,有效解决了标准水平集方法存在的一些问题。Wei和Wang[47]基于分段水平集方法提出了新的分段水平集拓扑优化方法,但该种方法用来处理多材料问题的优化才更能体现其优势。
3)ESO方法 ESO方法由Xie和Steven[13]在1993年提出,是近年来兴起的一种基于进化策略的优化方法。该方法采用有限元法对设计空间进行离散化处理,离散网格所对应的单元作为设计变量,并采用“零”和“非零”对其进行编码,在位移、应力、频率、临界压力和刚度的约束下,通过设计合适的准则评估单元对目标函数变化的贡献值,并以此为依据对材料单元进行增删,从而逐渐逼近最佳的结构布局形式。相较于SIMP方法,ESO法能够获得清晰的0-1材料分布。最初的ESO方法亦可称为“硬杀法”(Hard Kill),即直接删除应变能密度最低的单元。随后,该方法被进一步改进为双向进化结构优化法(BESO: Bi-directional EvolutionaryStructural Optimization)[29,30],按照设定的规则删除和复活单元,实现结构拓扑的变化。尽管最初的ESO方法多依赖于直觉性,但随着研究的深入,类似于变密度法中的共轭梯度分析法和过滤技术也逐步被引入[31],以增强算法和优化结果的稳定性。ESO方法符合工程直观性,应用简单方便,目前已被成功用于解决不同类型的拓扑优化问题[32-34]。 4) 水平集方法 均匀化方法、SIMP方法以及进化结构法都是属于基于材料分布的拓扑优化方法,而冒泡法则属于基于几何边界的拓扑优化方法。基于几何边界的拓扑优化方法分为两类:隐式边界描述方法和显式边界描述方法,冒泡法属于典型的显式边界描述方法,而水平集方法则属于典型的隐式边界描述方法,同显式边界描述方法相比,隐式边界描述具有很多优点,如:不需要重新划分网格,能够同时描述结构的拓扑和形状变化等。 水平集方法是Osher和Sethian[35]1988年在研究曲线(或曲面)以曲率相关的速度演化时候提出来的,是描述曲线(或曲面)演化过程的一种方法。其主要思想就是引入水平集函数,将移动界面作为的零等值面嵌入到高一维的水平集函数中。在演化过程中,演化曲线(或曲面)总是对应于该零等值线(或面),只要确定零等值线(或面)即可确定移动界面的位置。 由于水平集方法在模型描述方面有许多优点,2000年Sethian和Wiegmann[36]首先将水平集方法引入到结构拓扑优化领域中,用来进行等应力结构的设计,发展了一种高边界分辨率的刚性结构拓扑优化方法。Wang等[16,37,38]扩展了水平集拓扑形状优化的方法,将水平集方法和形状导数结合起来,通过结构边界的法向速度建立了Hamilton-Jacobi偏微分方程同形状导数之间的关系,采用逆风策略来求解水平集方程,实现结构边界的演化直至获得最优解。Allaire等[17,39]提出了一种相似的水平集拓扑形状优化方法,其边界速度场是从严格的形状敏度分析中推导出来的,边界的演化通过Hamilton-Jacobi方程来实现,其后又将该方法应用到结构特征频率问题拓扑优化以及柔性机构拓扑优化等方面。 为了提高水平集方法的优化收敛速度,提高效率,减少因为逆风差分格式中CFL条件的限制而增加的计算消耗,几种改进的水平集方法被提了出来,例如:Belytschko等[40]提出了规则化隐函数的水平集拓扑形状优化方法,其通过优化策略直接更新一个窄带上的水平集函数的结点值来实现边界演化。Haber等[41]将序列二次规划法和多级网格细化法结合提出了一种改进的水平集方法来进行结构特征频率形状优化。Amstutz和Andra[42]提出一种拓扑导数概念的水平集方法拓扑优化方法。Xia等[43]提出了一种半拉格朗日的水平集方法,摆脱步长限制,很好地提高了优化效率,但该方法稳定性比较差。Chen等[44]将R函数和B样条曲线函数结合提出一种隐式边界描述的具有参数控制和拓扑变化的形状优化方法。Wang S Y等[45]将径向基函数引入到水平集方法中,用参数化的径向基函数代替原来的离散水平集函数描述方法,将原来水平集优化方法中的Hamilton-Jacobi偏微分方程转换成了常微分方程,摆脱了CFL条件的步长限制,有效提高了求解效率。Luo Z等[46]在径向基函数方法的基础上采用紧支径向基函数(CS-RBF)建立了一种参数化的水平集方法,以插值函数扩展系数作为设计变量,并采用最优化准则法更新设计变量,有效解决了标准水平集方法存在的一些问题。Wei和Wang[47]基于分段水平集方法提出了新的分段水平集拓扑优化方法,但该种方法用来处理多材料问题的优化才更能体现其优势。 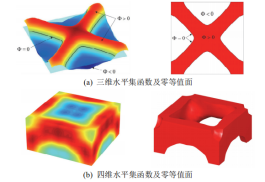 [1]Sokolowski J, Zolesio J P.Introduction to shape optimization: Shape sensitivity analysis. Springer-Verlag, New York, 1992 [2]Bendsoe M P. Optimization ofstructural topology, Shape and material. Springer-Verlag, Berlin, 1997
[1]Sokolowski J, Zolesio J P.Introduction to shape optimization: Shape sensitivity analysis. Springer-Verlag, New York, 1992 [2]Bendsoe M P. Optimization ofstructural topology, Shape and material. Springer-Verlag, Berlin, 1997