GPS定位算法(牛顿迭代+最小二乘 |
您所在的位置:网站首页 › 经纬度定位导航算法是什么意思 › GPS定位算法(牛顿迭代+最小二乘 |
GPS定位算法(牛顿迭代+最小二乘
|
第一步:准备数据与设置初始解 对于所有各颗可见卫星n,收集到它们在同一时刻的伪距测量值 同时,对于所有各颗可见卫星n,根据它们分星历计算出经过地球自转校正后的卫星空间位置坐标 在开始进行牛顿迭代之前,我们还需要给出接收机当前位置坐标的初始估计值 假如接收机在上一个定位时刻已经成功地解得定位结果,那么这次定位的初始估计值就自然可以采用上一个定位结果,包括接收机位置坐标与钟差值。如果我们还知道用户在上一个定位时刻的运动速度,那么据此推算出接收机当前位置的估计值也未尝不可。类似的,如果我们知道接收机适中的频漂,我们可以对钟差初始值进行类似的推算。这种情况对于接收机来说不仅最经常发生,而且通常也是最简单、最理想的一种。 然而,如果接收机在此前的近期一段时间内尚未实现定位,那么此刻对接收机来说是首次定位。对于首次定位,钟差初始值 (1)接收机一般允许用户输入其所在的位置和时间。如果用户确信其输入的位置坐标是大致正确的,那么该输入值就可以作为接收机位置坐标的初始估计值。这种外界输入值的含义其实是相当广泛的,它还可以是在接收机启动前就存留在接收机记忆单元中的定位值,也可以是由无线通信网络提供的辅助信息。 (2)接收机此时应该已经对多颗可见卫星进行了跟踪、测量,并计算了它们的空间位置。这样,我们可以计算出所有这些可见卫星位置坐标的平均值,然后将此平均值在地面的投影作为接收机位置坐标的初始估计值。 (3)接收机初始位置的各个坐标分量也可全部简单地设置为零。即便从零出发牛顿迭代法一般也只需几次迭代循环就可以得到收敛。 第二步:非线性方程组线性化 我们用k代表当前历元正在进行的牛顿迭代次数,即k-1是在当前历元已经完成的迭代次数,而k=1代表第一次迭代。 在当前历元的第k次牛顿迭代中,方程组
式1 的各个非线性方程可在 如图所示,
类似地,可以求出函数
式2 式1中左侧已经是一个关于
式3 其中 式4 而
式5 由G可见,雅可比矩阵G只是与各颗卫星相对于用户的几何位置有关,因而G通常被称为几何矩阵。 为了简化讨论,假设接收机时钟与GPS时间同步,而且该方程组的牛顿迭代法秩序迭代一次就得到收敛。考虑式3中的每一个方程式,其等号左边是单位观测矢量的反向与差值的内积,其中 与单位观测矢量反向的内积等于此位移在观测矢量反向上的投影。因此式3中的每一个方程式所代表的含义为:用户位移量在卫星观测反方向上的投影,等于由此位移引起的卫星与用户之间的距离变化量。伪距定位的过程,实际上是依据接收机到各个卫星的距离变化量来反推用户的运动位移矢量。
图2 用户位移在卫星观测方向上的投影 式3中的每个方程式关于接收机钟差的系数均为1,这是因为接收机钟差式各个卫星距离测量值中的公共偏差部分,它在定位计算中实际上是吸收向量b中各元素的平均值。 第3步:求解线性方程组 这一步的任务是利用最小二乘法求解GPS伪距定位线性矩阵方程式。套用最小二乘的求解公式,可得到最小二乘解为
如果各个卫星测量值的方差以及权重已被确定,那么也可以运用加权最小二乘法来求解。为了提高定位精度,一部分GPS接收机事实上采用加权最小二乘法作为GPS定位方程的求解算法。 第四步:更新非线性方程组的根 更新后的接收机坐标
第五步:判断牛顿迭代的收敛性 若牛顿迭代已经收敛到了所需要的精度,则牛顿迭代法可终止循环运算,并将当前这一次的迭代计算后的更新值作为接收机此时可的定位、定时结果;否则,k值增1,并返回至第二步再重复进行一次牛顿迭代计算。判断牛顿迭代是否收敛,一般可检查此次迭代计算得到的位移向量 牛顿迭代法有时会收敛到一个远离地球的天际一端。如果以上伪距定位计算给出的解与常识明显不符,那么GPS定位算法必须返回第一步,并恰当地调整接收机位置初始估计值,然后重新进行一次完成的牛顿迭代运算,使最后收敛至一个在地球表面附近的合理值为止。
|
【本文地址】
今日新闻 |
推荐新闻 |
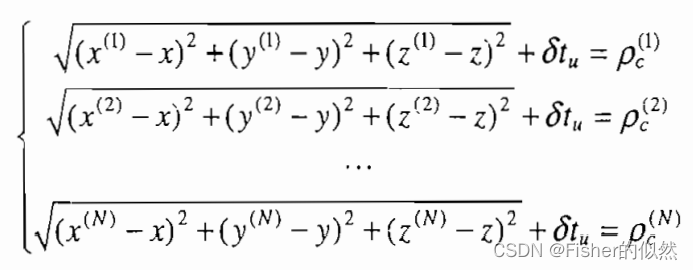
 图1 接收机指向卫星的观测矢量
图1 接收机指向卫星的观测矢量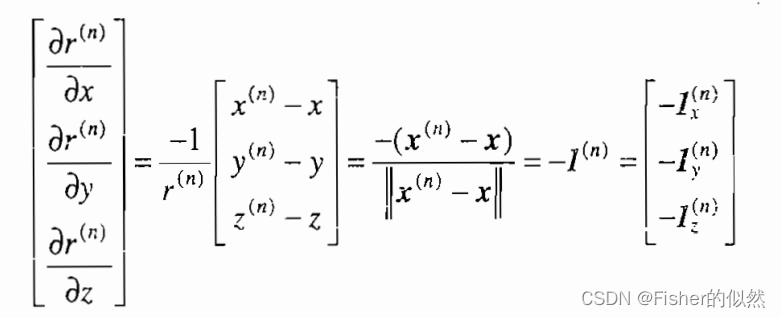

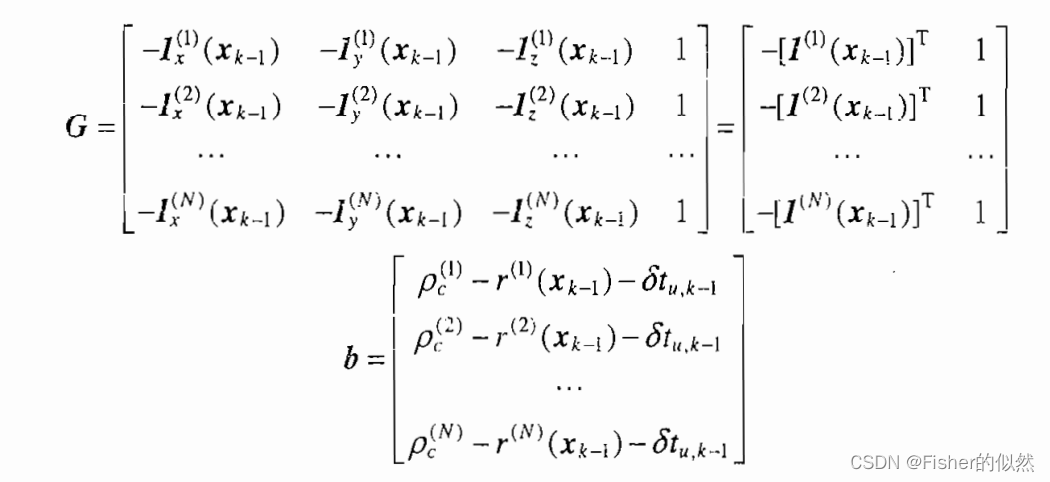
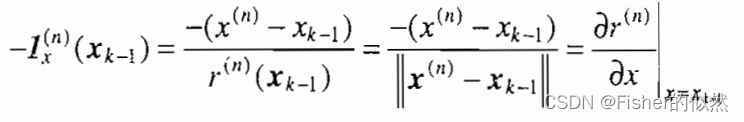

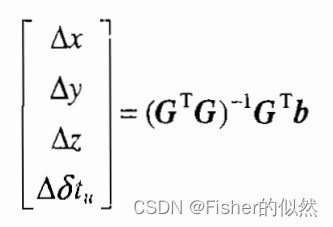
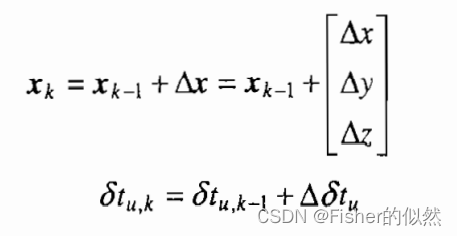
 的值是否已经小到一个预先设定的门限值。
的值是否已经小到一个预先设定的门限值。