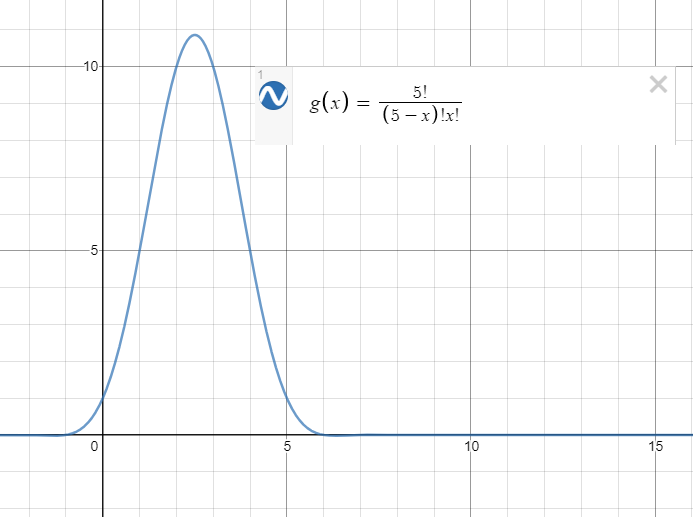
前排提示：本文数学公式较多，加载\(\LaTeX\)需要一定时间，可能会导致浏览器暂时卡顿，请耐心等待数学公式正常显示.

组合数学知识点的总结，本来准备写在一起的，结果发现字数有点多，导致\(\mathrm{markdown}\)编辑器频繁卡顿，那就分三篇发布好了.

\(\mathrm{Update}\)：目前第一篇就是组合基础和组合原理，预计第二篇基础高数，生成函数和特殊计数数列，第三篇多项式算法，至于会不会咕咕咕那就不知道了.

\(1.\) 用\(n!\)表示\(n\)的阶乘，\(n!=1\times 2\times \cdots \times n\)，用\(n^{\underline k}\)表示下降阶乘幂，简称下降幂，\(n^{\underline k}=n\times (n-1)\times \cdots \times (n-k+1)\)，用\(n^{\overline k}\)表示上升阶乘幂，简称上升幂，\(n^{\overline k}=n\times (n+1)\times \cdots\times (n+k-1)\).

\(2.\) 用\(\mathrm{A}_n^m\)表示从\(n\)个元素种选出\(m\)个组成的排列数量，称为排列数，\(\mathrm{A}_n^m=\frac{n!}{(n-m)!}\).

\(3.\) 用\(\mathrm{C}_n^m\)或\({n \choose m}\)表示从\(n\)个元素种选出\(m\)个组成的子集数量，称为组合数，\(\mathrm{C}_n^m={n\choose m}=\frac{n!}{m!(n-m)!}\).

\(4.\) 下降阶乘幂\(n^{\underline k}\)种\(n\)可以是任意实数，当我们将组合数\({r\choose k}\)定义改为\({r\choose k}=\frac{r^{\underline k}}{k!}\)时，称其为二项式系数，其中上指标可以为任意实数，下指标仍为整数，当下指标\(k>=1) if (b) Mul(res,a); return res; } inline int Inv(int x) { return fastpow( x , Mod - 2 ); } int inv[N],fac[N]; inline void Init(void) { inv[0] = fac[0] = 1; for (int i = 1; i = 1; i--) inv[i] = mul( inv[i+1] , i+1 ); } inline int C(int n,int m) { return ( m > n || n < 0 || m < 0 ) ? 0 : mul( fac[n] , mul( inv[m] , inv[n-m] ) ); } Lucas定理

当模数\(p\leq\max(m,n-m)\)时，组合数分母的\(m!(n-m)!\)就不存在逆元，此时我们需要用到\(\mathrm{Lucas}\)定理：

证明：

引理：\((1+x)^p\equiv1+x^p\pmod p,p\in \mathrm{Prime}\).

有费马小定理可知\((1+x)^p\equiv1+x\)，又因为\(x\equiv x^p\)，可知\((1+x)^p\equiv 1+x^p\).

用二项式定理展开上式中的三个二项式的幂：

左式取到\(x^m\)项系数为\({n\choose m}\)，右式取到\(x^m\)项系数当且仅当\(j=\left\lfloor\frac{m}{p}\right\rfloor,k=m\bmod p\)，对应项系数同余，所以就有：

回到上文，对于模数\(p\)较小时，只要\(p\)为质数，我们就可以运用\(\mathrm{Lucas}\)定理递归求解组合数，时间复杂度\(O(p)-O(\log_{p}n)\).

对于上指标确定的组合数，我们可以令\(f(x)={n\choose x}(n\in \N ^ +)\)，则函数\(f\)是单峰函数，其极值在\(x=\lfloor \frac{n}{2} \rfloor\)处取到.

两类阶乘幂可以提取因数\(-1\)进行互相转换：

从\(n\)个元素中选出\(m\)个排成圆圈的方案数，相当于线性排列时固定第一个数的方案。

一个循环排列可以对应\(m\)个线性排列，进而可以得到循环排列的计算公式：

若\(p\)为质数，则对于\(n\in[1,p-1]\)，有\(p\ |\ \binom{p}{n}\)。

证明：

\(1.\) 正整数解

求不定方程\(x_1+x_2+\cdots+x_k=n\)的正整数解的个数。

这个问题等价于把\(n\)个球放入\(k\)个盒子中，每个盒子中至少有\(1\)个球，由隔板法可知其方案数为\(\binom{n-1}{k-1}\)。

\(2.\) 非负整数解

求不定方程\(x_1+x_2+\cdots+x_k=n\)的非负整数解的个数。

我们可以新增\(k\)个球，这样问题就等价于把\(n+k\)个球放入\(k\)个盒子中，每个盒子中至少有\(1\)个球，由隔板法可知其方案数为\(\binom{n+k-1}{k-1}\)。

\(3.\) 下界限制

求不定方程\(x_1+x_2+\cdots+x_k=n\)的整数解的个数，满足\(x_1\geq a_1,x_2\geq a_2,\cdots,x_k\geq a_k\)。

这个问题等价于不定方程\(x_1+x_2+\cdots+x_k=n-a_1-a_2-\cdots-a_k\)的非负整数解个数，可以其方案数为$$\binom{n+k-1-\sum_{i=1}^{n}a_i}{k-1}$$

\(4.\) 上下界限制

求不定方程\(x_1+x_2+\cdots+x_k=n\)的整数解的个数，满足\(a_1\leq x_1\leq b_1,a_1\leq x_2\leq b_2,\cdots,a_k\leq x_k\leq b_k\)。

首先把限制转换为\(0\leq x_1\leq b_1-a_1,\cdots,0\leq x_k\leq b_k-a_k\)，运用容斥原理，答案即为：

多重集指含有重复元素的广义集合。设多重集\(S=\{n_1\times a_1,n_2\times a_2,\cdots,n_k\times a_k\}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)，\(...\)，\(n_k\)个\(a_k\)组成的集合，则\(S\)的全排列个数为

证明：

对于朴素全排列，显然有\(\left (\sum_{i=1}^k n\right )!\)种方案，而在多重集的排列过程中，每个\(a_i\)出现了\(n_i\)次，在这\(n_i\)个位置间各个\(a_i\)可以互相调换位置，有\(n_i!\)中方案，故除去每一个\(n_i\)可以调换位置的重复方案即为总排列数.

设多重集\(S=\{n_1\times a_1,n_2\times a_2,\cdots,n_k\times a_k\}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)，\(...\)，\(n_k\)个\(a_k\)组成的集合，从中取出\(r\left(r\leq\sum_{i=1}^{k}n_i\right)\)个元素可以组成不同集合个数为：

证明：

首先考虑\(r\leq\min\{n_i\}\)的情况，根据不定方程的非负整数解数量，可知答案为\({k+r-1\choose k-1}\).

然后可以考虑容斥原理，对于\(i\)，让选择\(a_i\)个数超出\(n_i\)成为一个性质，那么不具备任何性质的方案数即为上式.

定义离散函数的差分算子\((\Delta a)_i=a_i-a_{i-1}\)，则有：

证明：

容易在算子间定义四则运算，此处不再赘述.

定义平移算子\((\mathrm{E}a)_i=a_{i-1}\)，恒等算子\((\mathrm{I}a)_i=a_i\)，那么就有\(\Delta =\mathrm{I-E}\).

根据二项式定理展开：

取第\(i\)项就可以得到：

可以用多项式卷积算法求高阶差分序列的前\(n\)项.

对于组合数的下指标求和，即：

没有很好的封闭形式解，但是对于多组\((n,m)\)的询问，我们可以将\(n,m\)看作一个区间的左右端点，使用\(O(\max\{n_i,m_i\}\sqrt q)\)的莫队算法来求解.

考虑转移，对于\(m\rightarrow m+1\)，只需加上一个组合数\({n\choose m+1}\)即可. 对于\(n\rightarrow n+1\)，我们可以考虑用加法公式进行拆解：

于是区间移动可以\(O(1)\)处理了.

自然数幂和指的是这一类求和问题：

对于\(k\)比较小的情况，可以用组合恒等式推出通项公式.

对于\(k\)任意的情况，我们很难直接推出通项公式，但是可以通过多项式插值技巧求出答案，我们会在下文讨论这个问题.

鸽巢原理又称抽屉原理，形式化表述如下：

证明：

反证法，若不存在这样的盒子\(j\)，则对于任意的\(i\)都有\(a_i