【信号与系统】(八)连续系统的时域分析 |
您所在的位置:网站首页 › 线性相关系数计算公式例题 › 【信号与系统】(八)连续系统的时域分析 |
【信号与系统】(八)连续系统的时域分析
|
文章目录
相关函数1 互相关和自相关函数的定义2 相关与卷积的比较
相关函数
1 互相关和自相关函数的定义
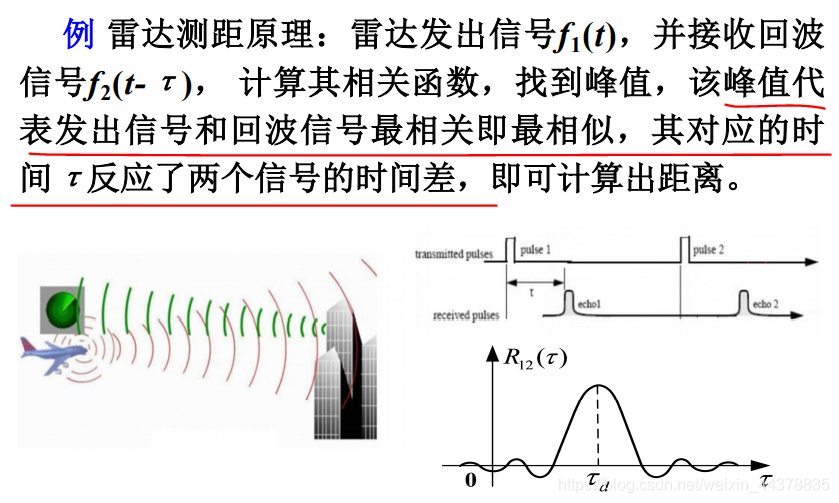
为比较某信号与另一延时 τ τ τ的信号之间的相似度,需要引入相关函数的概念。相关函数是鉴别信号的有力工具,被广泛应用于雷达回波的识别,通信同步信号的识别等领域。相关函数也称为相关积分,它与卷积的运算方法类似。 实函数 f 1 ( t ) f_1(t) f1(t)和 f 2 ( t ) f_2(t) f2(t),如为能量有限信号,它们之间的互相关函数定义为:
(注: R 12 , R 21 R_{12},R_{21} R12,R21下脚数字(12,21),前面数字代表的信号领先 τ τ τ) 互相关函数是两信号之间时间差
τ
τ
τ的函数。一般
R
12
(
τ
)
≠
R
21
(
τ
)
R_{12}(τ)≠ R_{21}(τ)
R12(τ)=R21(τ)。 如果
f
1
(
t
)
f_1(t)
f1(t)和
f
2
(
t
)
f_2(t)
f2(t)是同一信号,可记为
f
(
t
)
f(t)
f(t) ,这时无需区分
R
12
R_{12}
R12与
R
21
R_{21}
R21,用
R
(
τ
)
R(τ)
R(τ)表示,称为自相关函数。即 : 可见,实函数 f ( t ) f(t) f(t)的自相关函数是时移 τ τ τ的偶函数。 2 相关与卷积的比较
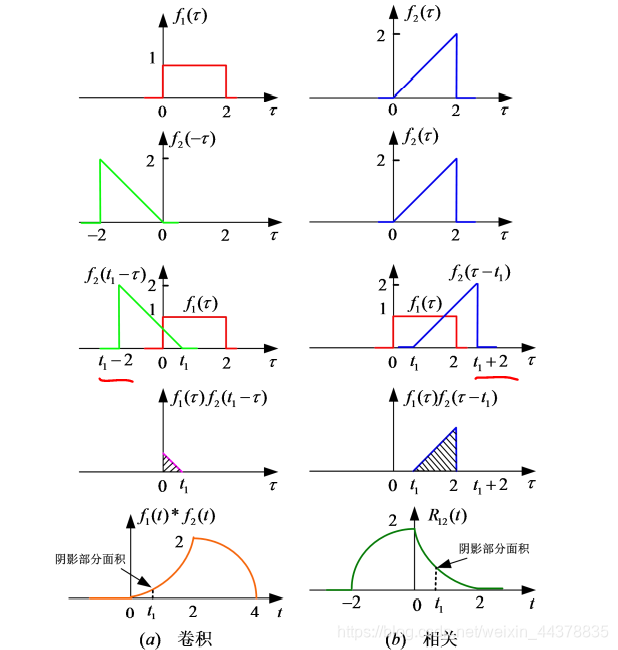
函数 f 1 ( t ) f_1(t) f1(t)和 f 2 ( t ) f_2(t) f2(t)卷积的表达式为: f 1 ( t ) ∗ f 2 ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( − ( τ − t ) ) d τ = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( t − τ ) d τ f_{1}(t) * f_{2}(t)=\int_{-\infty}^{\infty} f_{1}(\tau) f_{2}(-(\tau-t)) d \tau=\int_{-\infty}^{\infty} f_{1}(\tau) f_{2}(t-\tau) d \tau f1(t)∗f2(t)=∫−∞∞f1(τ)f2(−(τ−t))dτ=∫−∞∞f1(τ)f2(t−τ)dτ 为了便于与卷积函数进行比较,我们将互相关函数定义式中的变量 t t t和 τ τ τ进行互换,可将实函数 f 1 ( t ) f_1(t) f1(t)和 f 2 ( t ) f_2(t) f2(t)的互相关函数写为: R 12 ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( τ − t ) d τ R_{12}(t)=\int_{-\infty}^{\infty} f_{1}(\tau) f_{2}(\tau-t) d \tau R12(t)=∫−∞∞f1(τ)f2(τ−t)dτ 两种运算的不同之处:卷积开始时需要将 f 2 ( τ ) f_2(τ) f2(τ)反折为 f 2 ( − τ ) f_2(-τ) f2(−τ),而相关运算则不需反折,仍为 f 2 ( τ ) f_2(τ) f2(τ)。其他的移位、相乘和积分的运算方法相同
根据卷积的定义 由上式可知,若 f 1 ( t ) f_1(t) f1(t)和 f 2 ( t ) f_2(t) f2(t)均为实偶函数,则卷积与相关的形式完全相同 《工程信号与系统》作者:郭宝龙等 国家精品课程:信号与系统 ,中国大学MOOC,郭宝龙,朱娟娟 |
【本文地址】
今日新闻 |
推荐新闻 |

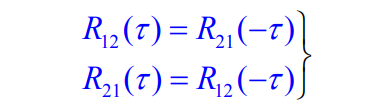
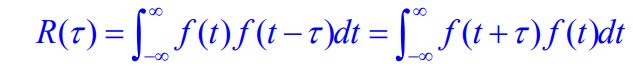 容易看出,对自相关函数有:
容易看出,对自相关函数有: 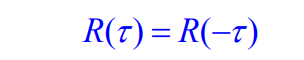
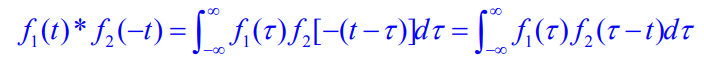 可见
可见