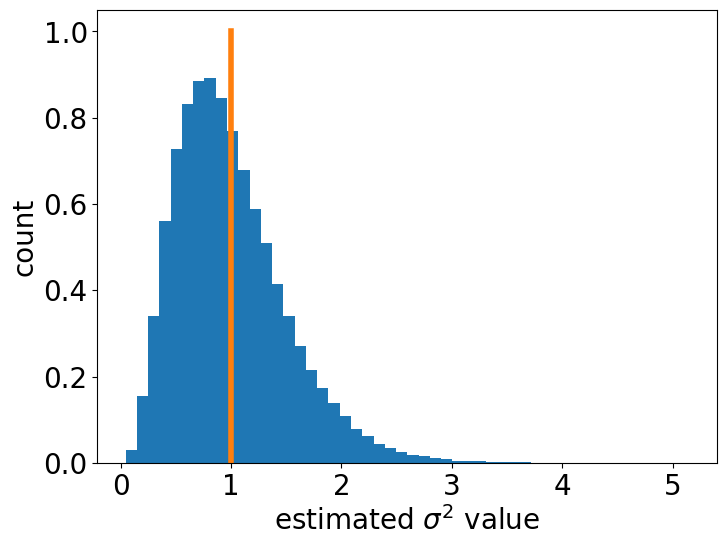
之前在文章线性回归系数的几个性质 中，我们证明了线性回归系数项的几个性质。在这篇短文中，我们介绍线性回归模型中误差项方差的估计。

我们先来回忆一下什么是线性回归的误差项。在文章线性回归系数的几个性质 中，我们指出，对于单变量的线性回归模型， y i = β 1 x i + β 0 + ϵ i ,   i = 1 ,   2 ,   ⋯   , n y_i = \beta_1 x_i + \beta_0 + \epsilon_i, \, i = 1, \, 2, \, \cdots, n yi​=β1​xi​+β0​+ϵi​,i=1,2,⋯,n， 其中 ϵ i \epsilon_i ϵi​ 为误差项 (error)，每个 ϵ i \epsilon_i ϵi​ 均是一个随机变量，独立且都服从 一个均值为0, 方差为 σ 2 \sigma^2 σ2 的概率分布。这篇短文介绍的就是对这个 σ 2 \sigma^2 σ2 的估计。

我们定义 S S R e s = ∑ i = 1 n e i 2 = ∑ i = 1 n ( y i − y i ^ ) 2 \displaystyle SS_{\mathrm{Res}} = \sum_{i = 1}^n e_i^2 = \sum_{i = 1}^n (y_i - \hat{y_i})^2 SSRes​=i=1∑n​ei2​=i=1∑n​(yi​−yi​^​)2。

首先，我们证明， S S R e s = ∑ i = 1 n y i 2 − n y ˉ 2 − β 1 ^ S x y SS_{\mathrm{Res}} = \sum_{i = 1}^n y_i^2 -n \bar{y}^2 - \hat{\beta_1} S_{xy} SSRes​=i=1∑n​yi2​−nyˉ​2−β1​^​Sxy​。

我们把 y i ^ = β 0 ^ + β 1 ^ ⋅ x i \displaystyle \hat{y_i} = \hat{\beta_0} + \hat{\beta_1} \cdot x_i yi​^​=β0​^​+β1​^​⋅xi​ 代入 S S R e s \displaystyle SS_{\mathrm{Res}} SSRes​ 的表达式。

我们有，

S S R e s = ∑ i = 1 n ( y i − y i ^ ) 2 = ∑ i = 1 n ( y i − ( β 0 ^ + β 1 ^ ⋅ x i ) ) 2 = ∑ i = 1 n y i 2 − 2 ∑ i = 1 n y i ( β 0 ^ + β 1 ^ ⋅ x i ) + ∑ i = 1 n ( β 0 ^ + β 1 ^ ⋅ x i ) 2 = ∑ i = 1 n y i 2 − 2 β 0 ^ ⋅ n y ˉ − 2 β 1 ^ ∑ i = 1 n x i y i + n β 0 ^ 2 + 2 β 0 ^ β 1 ^ ∑ i = 1 n x i + β 1 ^ 2 ∑ i = 1 n x i 2 = ∑ i = 1 n y i 2 − 2 ( y ˉ − β 1 ^ x ˉ ) n y ˉ − 2 β 1 ^ ∑ i = 1 n x i y i + n ( y ˉ − β 1 ^ x ˉ ) 2 + 2 ( y ˉ − β 1 ^ x ˉ ) β 1 ^ ∑ i = 1 n x i + β 1 ^ 2 ∑ i = 1 n x i 2 = ∑ i = 1 n y i 2 − 2 n y ˉ 2 + 2 n β 1 ^ x ˉ y ˉ − 2 β 1 ^ ∑ i = 1 n x i y i + n y ˉ 2 − 2 n β 1 ^ x ˉ y ˉ + n β 1 ^ 2 x ˉ 2 + 2 y ˉ β 1 ^ ∑ i = 1 n x i − 2 β 1 ^ 2 x ˉ ∑ i = 1 n x i + β 1 ^ 2 ∑ i = 1 n x i 2 = ∑ i = 1 n y i 2 − n y ˉ 2 − n β 1 ^ 2 x ˉ 2 + β 1 ^ 2 ∑ i = 1 n x i 2 − 2 β 1 ^ ∑ i = 1 n x i y i + 2 n β 1 ^ x ˉ y ˉ = ∑ i = 1 n y i 2 − n y ˉ 2 + β 1 ^ 2 ( ∑ i = 1 n x i 2 − n x ˉ 2 ) − 2 β 1 ^ ( ∑ i = 1 n x i y i − n x ˉ y ˉ ) = ∑ i = 1 n y i 2 − n y ˉ 2 + β 1 ^ 2 S x x − 2 β 1 ^ S x y = ∑ i = 1 n y i 2 − n y ˉ 2 + β 1 ^ ( S x y S x x ) S x x − 2 β 1 ^ S x y = ∑ i = 1 n y i 2 − n y ˉ 2 − β 1 ^ S x y \begin{aligned} \displaystyle SS_{\mathrm{Res}} &= \sum_{i = 1}^n (y_i - \hat{y_i})^2 = \sum_{i = 1}^n \big(y_i - (\hat{\beta_0} + \hat{\beta_1} \cdot x_i) \big)^2 \\ &= \sum_{i = 1}^n y_i^2 - 2 \sum_{i = 1}^n y_i (\hat{\beta_0} + \hat{\beta_1} \cdot x_i) + \sum_{i = 1}^n (\hat{\beta_0} + \hat{\beta_1} \cdot x_i)^2 \\ &= \sum_{i = 1}^n y_i^2 - 2 \hat{\beta_0} \cdot n \bar{y} - 2 \hat{\beta_1} \sum_{i = 1}^n x_i y_i + n \hat{\beta_0}^2 + 2 \hat{\beta_0} \hat{\beta_1} \sum_{i = 1}^n x_i + \hat{\beta_1}^2 \sum_{i = 1}^n x_i^2 \\ &= \sum_{i = 1}^n y_i^2 - 2 (\bar{y} - \hat{\beta_1} \bar{x}) n \bar{y} - 2 \hat{\beta_1} \sum_{i = 1}^n x_i y_i + n (\bar{y} - \hat{\beta_1} \bar{x})^2 + 2 (\bar{y} - \hat{\beta_1} \bar{x}) \hat{\beta_1} \sum_{i = 1}^n x_i + \hat{\beta_1}^2 \sum_{i = 1}^n x_i^2 \\ &= \sum_{i = 1}^n y_i^2 - 2 n \bar{y}^2 + 2n \hat{\beta_1} \bar{x} \bar{y} - 2 \hat{\beta_1} \sum_{i = 1}^n x_i y_i + n \bar{y}^2 - 2n \hat{\beta_1} \bar{x} \bar{y} + \\ & \hspace{5mm} n \hat{\beta_1}^2 \bar{x}^2 + 2 \bar{y} \hat{\beta_1} \sum_{i = 1}^n x_i - 2 \hat{\beta_1}^2 \bar{x} \sum_{i = 1}^n x_i + \hat{\beta_1}^2 \sum_{i = 1}^n x_i^2 \\ &= \sum_{i = 1}^n y_i^2 - n \bar{y}^2 - n \hat{\beta_1}^2 \bar{x}^2 + \hat{\beta_1}^2 \sum_{i = 1}^n x_i^2 - 2 \hat{\beta_1} \sum_{i = 1}^n x_i y_i + 2n \hat{\beta_1} \bar{x} \bar{y} \\ &= \sum_{i = 1}^n y_i^2 - n \bar{y}^2 + \hat{\beta_1}^2 \big( \sum_{i = 1}^n x_i^2 - n \bar{x}^2 \big) - 2 \hat{\beta_1} \big( \sum_{i = 1}^n x_i y_i - n \bar{x} \bar{y} \big) \\ &= \sum_{i = 1}^n y_i^2 - n \bar{y}^2 + \hat{\beta_1}^2 S_{xx} - 2 \hat{\beta_1} S_{xy} \\ &= \sum_{i = 1}^n y_i^2 - n \bar{y}^2 + \hat{\beta_1} \left( \frac{S_{xy} }{ S_{xx} } \right) S_{xx} - 2 \hat{\beta_1} S_{xy} \\ &= \sum_{i = 1}^n y_i^2 -n \bar{y}^2 - \hat{\beta_1} S_{xy} \end{aligned} SSRes​​=i=1∑n​(yi​−yi​^​)2=i=1∑n​(yi​−(β0​^​+β1​^​⋅xi​))2=i=1∑n​yi2​−2i=1∑n​yi​(β0​^​+β1​^​⋅xi​)+i=1∑n​(β0​^​+β1​^​⋅xi​)2=i=1∑n​yi2​−2β0​^​⋅nyˉ​−2β1​^​i=1∑n​xi​yi​+nβ0​^​2+2β0​^​β1​^​i=1∑n​xi​+β1​^​2i=1∑n​xi2​=i=1∑n​yi2​−2(yˉ​−β1​^​xˉ)nyˉ​−2β1​^​i=1∑n​xi​yi​+n(yˉ​−β1​^​xˉ)2+2(yˉ​−β1​^​xˉ)β1​^​i=1∑n​xi​+β1​^​2i=1∑n​xi2​=i=1∑n​yi2​−2nyˉ​2+2nβ1​^​xˉyˉ​−2β1​^​i=1∑n​xi​yi​+nyˉ​2−2nβ1​^​xˉyˉ​+nβ1​^​2xˉ2+2yˉ​β1​^​i=1∑n​xi​−2β1​^​2xˉi=1∑n​xi​+β1​^​2i=1∑n​xi2​=i=1∑n​yi2​−nyˉ​2−nβ1​^​2xˉ2+β1​^​2i=1∑n​xi2​−2β1​^​i=1∑n​xi​yi​+2nβ1​^​xˉyˉ​=i=1∑n​yi2​−nyˉ​2+β1​^​2(i=1∑n​xi2​−nxˉ2)−2β1​^​(i=1∑n​xi​yi​−nxˉyˉ​)=i=1∑n​yi2​−nyˉ​2+β1​^​2Sxx​−2β1​^​Sxy​=i=1∑n​yi2​−nyˉ​2+β1​^​(Sxx​Sxy​​)Sxx​−2β1​^​Sxy​=i=1∑n​yi2​−nyˉ​2−β1​^​Sxy​​

于是，我们就证明了 S S R e s = ∑ i = 1 n y i 2 − n y ˉ 2 − β 1 ^ S x y SS_{\mathrm{Res}} = \sum_{i = 1}^n y_i^2 -n \bar{y}^2 - \hat{\beta_1} S_{xy} SSRes​=i=1∑n​yi2​−nyˉ​2−β1​^​Sxy​。

下面我们来看残差平方和的期望，即 E [ S S R e s ] \displaystyle \mathbb{E} [ SS_{\mathrm{Res}} ] E[SSRes​] 。

E [ S S R e s ] = E [ ∑ i = 1 n y i 2 ] − n E [ y ˉ 2 ] − E [ β 1 ^ S x y ] \displaystyle \mathbb{E} [ SS_{\mathrm{Res}} ] = \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big] - n \mathbb{E} \big[ \bar{y}^2 \big] - \mathbb{E} \big[ \hat{\beta_1} S_{xy} \big] E[SSRes​]=E[i=1∑n​yi2​]−nE[yˉ​2]−E[β1​^​Sxy​]。

我们分项来求。

我们先来求 E [ ∑ i = 1 n y i 2 ] \displaystyle \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big] E[i=1∑n​yi2​]。我们知道， E [ y i ] = E [ β 1 x i + β 0 + ϵ i ] = β 1 x i + β 0 \displaystyle \mathbb{E} \big[ y_i \big] = \mathbb{E} \big[ \beta_1 x_i + \beta_0 + \epsilon_i \big] = \beta_1 x_i + \beta_0 E[yi​]=E[β1​xi​+β0​+ϵi​]=β1​xi​+β0​。注意这里我们用到了 E [ ϵ i ] = 0 \displaystyle \mathbb{E} \big[ \epsilon_i \big] = 0 E[ϵi​]=0。 而 V a r [ ϵ i ] = σ 2 \displaystyle \mathrm{Var} \big[ \epsilon_i \big] = \sigma^2 Var[ϵi​]=σ2。于是，我们知道 V a r [ y i ] = σ 2 \displaystyle \mathrm{Var} \big[ y_i \big] = \sigma^2 Var[yi​]=σ2。从而， E [ y i 2 ] = V a r [ y i ] + ( E [ y i ] ) 2 = ( β 1 x i + β 0 ) 2 + σ 2 \displaystyle \mathbb{E} \big[ y_i^2 \big] = \mathrm{Var} \big[ y_i \big] + (\mathbb{E} \big[ y_i \big])^2 = (\beta_1 x_i + \beta_0)^2 + \sigma^2 E[yi2​]=Var[yi​]+(E[yi​])2=(β1​xi​+β0​)2+σ2。 E [ ∑ i = 1 n y i 2 ] = ∑ i = 1 n ( ( β 1 x i + β 0 ) 2 + σ 2 ) = ∑ i = 1 n ( β 1 x i + β 0 ) 2 + n σ 2 \displaystyle \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big] = \sum_{i = 1}^n \big( (\beta_1 x_i + \beta_0)^2 + \sigma^2 \big) = \sum_{i = 1}^n (\beta_1 x_i + \beta_0)^2 + n \sigma^2 E[i=1∑n​yi2​]=i=1∑n​((β1​xi​+β0​)2+σ2)=i=1∑n​(β1​xi​+β0​)2+nσ2。

对于 E [ y ˉ 2 ] \displaystyle \mathbb{E} \big[ \bar{y}^2 \big] E[yˉ​2]，我们采用一样的方法。因为 E [ y ˉ ] = 1 n ∑ i = 1 n ( β 1 x i + β 0 ) = β 0 + β 1 x ˉ \displaystyle \mathbb{E} \big[ \bar{y} \big] = \frac{1}{n} \sum_{i = 1}^n (\beta_1 x_i + \beta_0) = \beta_0 + \beta_1 \bar{x} E[yˉ​]=n1​i=1∑n​(β1​xi​+β0​)=β0​+β1​xˉ。 V a r [ y ˉ ] = 1 n 2 ∑ i = 1 n V a r [ y i ] = 1 n 2 ⋅ n σ 2 = σ 2 n \displaystyle \mathrm{Var} \big[ \bar{y} \big] = \frac{1}{n^2} \sum_{i = 1}^n \mathrm{Var} \big[ y_i \big] = \frac{1}{n^2} \cdot n \sigma^2 = \frac{\sigma^2}{n} Var[yˉ​]=n21​i=1∑n​Var[yi​]=n21​⋅nσ2=nσ2​。 于是， E [ y ˉ 2 ] = V a r [ y ˉ ] + ( E [ y ˉ ] ) 2 = σ 2 n + ( β 0 + β 1 x ˉ ) 2 \displaystyle \mathbb{E} \big[ \bar{y}^2 \big] = \mathrm{Var} \big[ \bar{y} \big] + \big( \mathbb{E} \big[ \bar{y} \big] \big)^2 =\frac{\sigma^2}{n} + ( \beta_0 + \beta_1 \bar{x} )^2 E[yˉ​2]=Var[yˉ​]+(E[yˉ​])2=nσ2​+(β0​+β1​xˉ)2。

对于最后一项， E [ β 1 ^ S x y ] \mathbb{E} \big[ \hat{\beta_1} S_{xy} \big] E[β1​^​Sxy​]，因为 β 1 ^ = S x y S x x \displaystyle \hat{\beta_1} = \frac{S_{xy} }{ S_{xx} } β1​^​=Sxx​Sxy​​，而 S x x S_{xx} Sxx​ 是常数，所以我们须要求 E [ S x y 2 ] \displaystyle \mathbb{E} \big[ S_{xy}^2 \big] E[Sxy2​]。 注意到， S x y = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) = ∑ i = 1 n ( x i − x ˉ ) y i \displaystyle S_{xy} = \sum_{i = 1}^n (x_i - \bar{x}) (y_i - \bar{y}) =\sum_{i = 1}^n (x_i - \bar{x}) y_i Sxy​=i=1∑n​(xi​−xˉ)(yi​−yˉ​)=i=1∑n​(xi​−xˉ)yi​。

我们有 E [ ∑ i = 1 n ( x i − x ˉ ) y i ] = ∑ i = 1 n ( x i − x ˉ ) ⋅ E [ y i ] = ∑ i = 1 n ( x i − x ˉ ) ( β 0 + β 1 x i ) \displaystyle \mathbb{E} \big[ \sum_{i = 1}^n (x_i - \bar{x}) y_i \big] = \sum_{i = 1}^n (x_i - \bar{x}) \cdot \mathbb{E} \big[ y_i \big] = \sum_{i = 1}^n (x_i - \bar{x}) (\beta_0 + \beta_1 x_i) E[i=1∑n​(xi​−xˉ)yi​]=i=1∑n​(xi​−xˉ)⋅E[yi​]=i=1∑n​(xi​−xˉ)(β0​+β1​xi​)。 另外， V a r [ ∑ i = 1 n ( x i − x ˉ ) y i ] = ∑ i = 1 n ( x i − x ˉ ) 2 ⋅ V a r [ y i ] = ∑ i = 1 n ( x i − x ˉ ) 2 σ 2 \displaystyle \mathrm{Var} \big[ \sum_{i = 1}^n (x_i - \bar{x}) y_i \big] = \sum_{i = 1}^n (x_i - \bar{x})^2 \cdot \mathrm{Var} \big[ y_i \big] = \sum_{i = 1}^n (x_i - \bar{x})^2 \sigma^2 Var[i=1∑n​(xi​−xˉ)yi​]=i=1∑n​(xi​−xˉ)2⋅Var[yi​]=i=1∑n​(xi​−xˉ)2σ2。这里我们用到了 y i ,   i = 1 ,   2 ,   ⋯ n y_i, \, i = 1, \, 2, \, \cdots n yi​,i=1,2,⋯n 是非相关的 (uncorrelated)。 从而， E [ S x y 2 ] = E [ ( ∑ i = 1 n ( x i − x ˉ ) y i ) 2 ] = V a r [ ∑ i = 1 n ( x i − x ˉ ) y i ] + ( E [ ∑ i = 1 n ( x i − x ˉ ) y i ] ) 2 = ∑ i = 1 n ( x i − x ˉ ) 2 σ 2 + ( ∑ i = 1 n ( x i − x ˉ ) ( β 0 + β 1 x i ) ) 2 = S x x σ 2 + ( ∑ i = 1 n β 1 x i ( x i − x ˉ ) ) 2 = S x x σ 2 + β 1 2 S x x 2 \begin{aligned} \displaystyle \mathbb{E} \big[ S_{xy}^2 \big] &= \mathbb{E} \big[ \big( \sum_{i = 1}^n (x_i - \bar{x}) y_i \big)^2 \big] \\ &= \mathrm{Var} \big[ \sum_{i = 1}^n (x_i - \bar{x}) y_i \big] + \left( \mathbb{E} \big[ \sum_{i = 1}^n (x_i - \bar{x}) y_i \big] \right)^2 \\ &= \sum_{i = 1}^n (x_i - \bar{x})^2 \sigma^2 + \left( \sum_{i = 1}^n (x_i - \bar{x}) (\beta_0 + \beta_1 x_i) \right)^2 \\ &= S_{xx} \sigma^2 + \left( \sum_{i = 1}^n \beta_1 x_i (x_i - \bar{x}) \right)^2 \\ &= S_{xx} \sigma^2 + \beta_1^2 S_{xx}^2 \end{aligned} E[Sxy2​]​=E[(i=1∑n​(xi​−xˉ)yi​)2]=Var[i=1∑n​(xi​−xˉ)yi​]+(E[i=1∑n​(xi​−xˉ)yi​])2=i=1∑n​(xi​−xˉ)2σ2+(i=1∑n​(xi​−xˉ)(β0​+β1​xi​))2=Sxx​σ2+(i=1∑n​β1​xi​(xi​−xˉ))2=Sxx​σ2+β12​Sxx2​​

从而， E [ β 1 ^ S x y ] = S x x σ 2 + β 1 2 S x x 2 S x x = σ 2 + β 1 2 S x x \displaystyle \mathbb{E} \big[ \hat{\beta_1} S_{xy} \big] = \frac{ S_{xx} \sigma^2 + \beta_1^2 S_{xx}^2 }{ S_{xx}} = \sigma^2 + \beta_1^2 S_{xx} E[β1​^​Sxy​]=Sxx​Sxx​σ2+β12​Sxx2​​=σ2+β12​Sxx​。

我们把， E [ ∑ i = 1 n y i 2 ] ,   E [ y ˉ 2 ] ,   [ S x y 2 ] \displaystyle \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big], \, \mathbb{E} \big[ \bar{y}^2 \big], \, \big[ S_{xy}^2 \big] E[i=1∑n​yi2​],E[yˉ​2],[Sxy2​] 这三项代入 E [ S S R e s ] = E [ ∑ i = 1 n y i 2 ] − n E [ y ˉ 2 ] − E [ β 1 ^ S x y ] \displaystyle \mathbb{E} [ SS_{\mathrm{Res}} ] = \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big] - n \mathbb{E} \big[ \bar{y}^2 \big] - \mathbb{E} \big[ \hat{\beta_1} S_{xy} \big] E[SSRes​]=E[i=1∑n​yi2​]−nE[yˉ​2]−E[β1​^​Sxy​]。 我们有 E [ S S R e s ] = E [ ∑ i = 1 n y i 2 ] − n E [ y ˉ 2 ] − E [ β 1 ^ S x y ] = ∑ i = 1 n ( β 1 x i + β 0 ) 2 + n σ 2 − n ( σ 2 n + ( β 0 + β 1 x ˉ ) 2 ) − ( σ 2 + β 1 2 S x x ) = ( n − 2 ) σ 2 \begin{aligned} \displaystyle \mathbb{E} [ SS_{\mathrm{Res}} ] &= \mathbb{E} \big[ \sum_{i = 1}^n y_i^2 \big] - n \mathbb{E} \big[ \bar{y}^2 \big] - \mathbb{E} \big[ \hat{\beta_1} S_{xy} \big] \\ &= \sum_{i = 1}^n (\beta_1 x_i + \beta_0)^2 + n \sigma^2 - n \left( \frac{\sigma^2}{n} + ( \beta_0 + \beta_1 \bar{x} )^2 \right) - ( \sigma^2 + \beta_1^2 S_{xx} ) \\ &= (n - 2) \sigma^2 \end{aligned} E[SSRes​]​=E[i=1∑n​yi2​]−nE[yˉ​2]−E[β1​^​Sxy​]=i=1∑n​(β1​xi​+β0​)2+nσ2−n(nσ2​+(β0​+β1​xˉ)2)−(σ2+β12​Sxx​)=(n−2)σ2​

也就是说， S S R e s n − 2 \displaystyle \frac{ SS_{\mathrm{Res}} }{n - 2} n−2SSRes​​ 是 σ 2 \sigma^2 σ2 的一个无偏估计。

res np.mean(res)

1.0004110047596488

我们发现， S S R e s n − 2 \displaystyle \frac{ SS_{\mathrm{Res}} }{n - 2} n−2SSRes​​ 的均值非常接近 σ 2 \sigma^2 σ2

事实上， ( n − 2 ) S S R e s / σ 2 \displaystyle (n - 2) SS_{\mathrm{Res}} / \sigma^2 (n−2)SSRes​/σ2 服从的是 χ n − 2 2 \chi^2_{n - 2} χn−22​ 的分布 [1]。

[1] Introduction to linear regression analysis, Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining, John Wiley & Sons (2021)