K |
您所在的位置:网站首页 › 算法三个基本要素组成 › K |
K
|
文章目录
1.K-近邻算法小例子评价
2.K-近邻模型2.1 距离度量
L
p
L_p
Lp距离欧氏距离(Euclidean Distance)曼哈顿距离(Manhattan Distance)其它
2.2
k
\large k
k 值的选择不同k值的影响特例:
k
=
1
k=1
k=1(最近邻算法)特例:
k
=
N
k=N
k=Nk值选择
2.3 分类决策规则
3. 代码实现kNN的完整实现
4. 实际应用
1.K-近邻算法
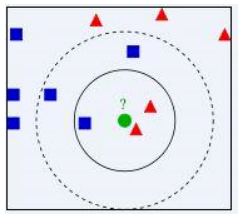
K近邻(K-Nearest Neighbor, KNN)是一种最经典和最简单的有监督学习方法之一。K-近邻算法是最简单的分类器,没有显式的学习过程或训练过程,是懒惰学习(Lazy Learning)。当对数据的分布只有很少或者没有任何先验知识时,K 近邻算法是一个不错的选择。 K近邻算法既能够用来解决分类问题,也能够用来解决回归问题。该方法有着非常简单的原理:当对测试样本进行分类时,首先通过扫描训练样本集,找到与该测试样本最相似的个训练样本,根据这个样本的类别进行投票确定测试样本的类别。也可以通过个样本与测试样本的相似程度进行加权投票。如果需要以测试样本对应每类的概率的形式输出,可以通过个样本中不同类别的样本数量分布来进行估计。 三个基本要素 k \large k k 值的选择、距离度量和分类决策规则 为什么不具有显式的学习过程或训练过程? 小例子 简单说就是如果测试样本在特征空间中的k个最邻近的样本中,大多数样本属于某个类别,则该测试样本也划分到这个类别,KNN里的K就是最邻近的K个数据样本。
要确定绿圆属于哪个类别,如果k=3,在其最近的3个样本中红色三角形数量最多,绿圆属于红色三角形类别,如果k=5,在其最近的5个样本中蓝色矩形数量最多,绿圆属于蓝色矩形类别,可见k的选择很重要(k的选择我们后面再讨论)。 评价在对测试样本进行预测时,因为只用到训练样本中与其最接近的K个 样本,K近邻算法的偏置(Bias)往往很低,而方差(Variance)则 很高。当训练集较小的时候,K近邻算法易出现过拟合。 2.K-近邻模型KNN中,当训练集、距离度量、k值及分类决策规则确定后,对于任何一个新的输入实例,它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类。 单元(cell):特征空间中对每个训练实例点x,距离该点比其他点更近的所有点组成的一个区域叫做单元。 类标记( classlabel):每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分。❎最近邻法将实例 x i \large x_i xi的类 y i \large y_i yi作为其单元中所有点的类标记( classlabel)。这样,每个单元的实例点的类别是确定的。图3.1是二维特征空间划分的一个例子。 2.1 距离度量 特征空间中两个实例点之间的距离是二者相似程度的反应,所以K近邻算法中一个重要的问题是计算样本之间的距离,以确定训练样本中哪些样本与测试样本更加接近。 在实际应用中,我们往往需要根据应用的场景和数据本身的特点来选择距离计算方法。当已有的距离方法不能满足实际应用需求时,还需要针对性地提出适合具体问题的距离度量方法。 L p L_p Lp距离
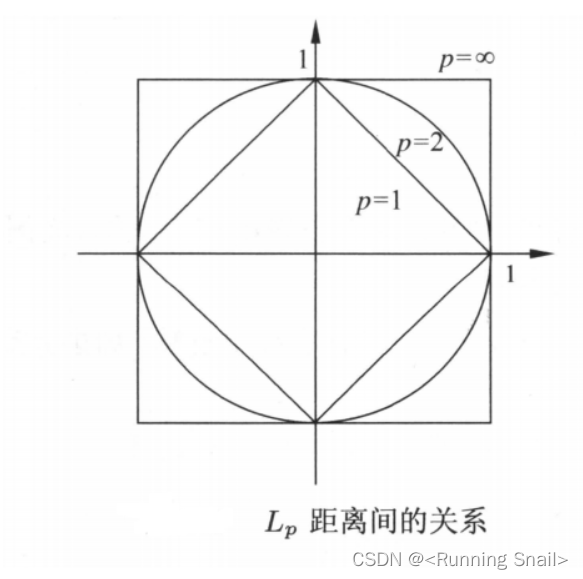
当 p = 2 p = 2 p=2,为欧氏距离(Euclidean Distance) 当 p = 1 p = 1 p=1,为曼哈顿距离(Manhattan Distance) 当 p = ∞ p = ∞ p=∞,为各个坐标距离的最大值 下图为二维空间中,与原点的 L p L_p Lp距离为1的点的图形( L p = 1 L_p = 1 Lp=1)
欧氏距离是最常见的距离度量,衡量的是多维空间中两个样本点之间的绝对距离。假设多维空间的维度为 N N N, x 1 = x 11 , x 12 , ⋯ , x 1 N \large x_1 = {x_{11},x_{12},\cdots, x_{1N}} x1=x11,x12,⋯,x1N 和 x 2 = x 21 , x 22 , ⋯ , x 2 N \large x_2 = {x_{21},x_{22},\cdots, x_{2N}} x2=x21,x22,⋯,x2N 是两个样本点,则 x 1 \large x_1 x1和 x 2 \large x_2 x2之间的欧氏距离计算公式为 L 2 ( x 1 , x 2 ) = ∑ n = 1 N ( x 1 n − x 2 n ) 2 \Large L_2(x_1, x_2) = \sqrt[]{\sum_{n=1}^{N}(x_{1n} - x_{2n})^2} L2(x1,x2)=∑n=1N(x1n−x2n)2 可见,欧氏距离由两个样本之间每一维度之差的平方和计算而来。当维度之间的取值范围差别太大时,欧氏距离容易被那些取值范围大的变量所主导,从而会大大降低模型的效果。因此,在实际应用K近邻算法来解决分类等问题时,如果采用欧氏距离作为相似度度量,最好提前对数据进行标准化转换。 曼哈顿距离(Manhattan Distance) 曼哈顿距离,也被称为出租车几何,是一种用来度量多维维实数空间内两个样本点之间距离的方法。假设多维空间的维度为 N N N, x 1 = x 11 , x 12 , ⋯ , x 1 N \large x_1 = {x_{11},x_{12},\cdots, x_{1N}} x1=x11,x12,⋯,x1N 和 x 2 = x 21 , x 22 , ⋯ , x 2 N \large x_2 = {x_{21},x_{22},\cdots, x_{2N}} x2=x21,x22,⋯,x2N 是两个样本点,则 x 1 \large x_1 x1和 x 2 \large x_2 x2之间的欧氏距离计算公式为 L 1 ( x 1 , x 2 ) = ∑ n = 1 N ∣ x 1 n − x 2 n ∣ \Large L_1(x_1, x_2) = \sum_{n=1}^{N}\left|x_{1n} - x_{2n}\right| L1(x1,x2)=∑n=1N x1n−x2n 曼哈顿距离等于两个样本之间每一维度之差的绝对值之和。曼哈顿距离的含义可以对应到规划为方框建筑的城市(如曼哈顿),两个地点的出租车最短行驶距离。在使用曼哈顿距离时,也需要考虑变量之间取值范围不同对结果的影响。 其它 当已有距离度量方法不能满足需求时,可以探索符合需求的距离度量方法。 实际的数据中,往往是离散型变量和连续型变量同时存在,如何计算这种混合变量下的样本相似度是一个开放性的问题。一种简单的方法是,在进行距离计算之前对样本中的离散型变量进行One-Hot编码,然后选取上述介绍的距离计算方法进行处理。 2.2 k \large k k 值的选择 不同k值的影响一般而言,从 k = 1 k = 1 k=1开始,随着的逐渐增大,K近邻算法的分类效果会逐渐提升;在增大到某个值后,随着的进一步增大,K近邻算法的分类效果会逐渐下降。 k值较小,相当于用较小的邻域中的训练实例进行预测,只有距离近的(相似的)起作用 单个样本影响大 “学习”的近似误差(approximation error)会减小,但估计误差(estimation error)会增大 噪声敏感 整体模型变得复杂,容易发生过拟合 k值较大,这时距离远的(不相似的)也会起作用 近似误差会增大,但估计误差会减小 整体的模型变得简单 特例: k = 1 k=1 k=1(最近邻算法)此时,KNN的泛化错误率上界为贝叶斯最优分类器错误率的两倍(证明见最后) 特例: k = N k=N k=NK近邻算法对每一个测试样本的预测结果将会变成一样(属于训练样例中最多的类)。 k值选择 一般k值较小。k通常取奇数,避免产生相等占比的情况。往往需要通过**交叉验证(Cross Validation)**等方法评估模型在不同取值下的性能,进而确定具体问题的K值。 2.3 分类决策规则 一般都是多数表决规则(majority voting rule),即把k个邻近的多数类别作为测试样本的类别 3. 代码实现 kNN的完整实现1)确定K的大小和距离计算方法 2)从训练样本中得到K个与测试最相似的样本 ①计算测试数据与各个训练数据之间的距离; ②按照距离的递增关系进行排序; ③选取距离最小的K个点; ④确定前K个点所在类别的出现频率; ⑤返回前K个点中出现频率最高的类别作为测试数据的预测分类。 3)根据K个组相似样本的类别,通过投票的方式来确定测试样本的类别 import csv import random import math import operator # 加载数据集 def loadDataset(filename, split, trainingSet = [], testSet = []): with open(filename, 'r') as csvfile: lines = csv.reader(csvfile) dataset = list(lines) for x in range(len(dataset)-1): for y in range(4): dataset[x][y] = float(dataset[x][y]) if random.random() |
【本文地址】
今日新闻 |
推荐新闻 |