一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇) |
您所在的位置:网站首页 › 简述bp算法的主要思想 › 一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇) |
一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇)
|
欢迎大家关注我们的网站和系列教程:http://www.tensorflownews.com/,学习更多的机器学习、深度学习的知识! 反向传播算法(Backpropagation Algorithm,简称BP算法)是深度学习的重要思想基础,对于初学者来说也是必须要掌握的基础知识!本文希望以一个清晰的脉络和详细的说明,来让读者彻底明白BP算法的原理和计算过程。 全文分为上下两篇,上篇主要介绍BP算法的原理(即公式的推导),介绍完原理之后,我们会将一些具体的数据带入一个简单的三层神经网络中,去完整的体验一遍BP算法的计算过程;下篇是一个项目实战,我们将带着读者一起亲手实现一个BP神经网络(不适用任何第三方的深度学习框架)来解决一个具体的问题。 读者在学习的过程中,有任何的疑问,欢迎加入我们的交流群(扫描文章最后的二维码即可加入),和大家一起讨论! 1. BP算法的推导
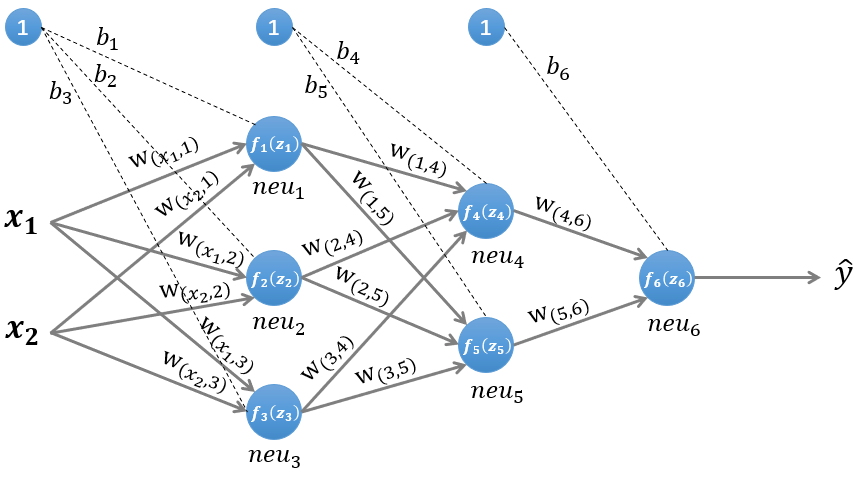
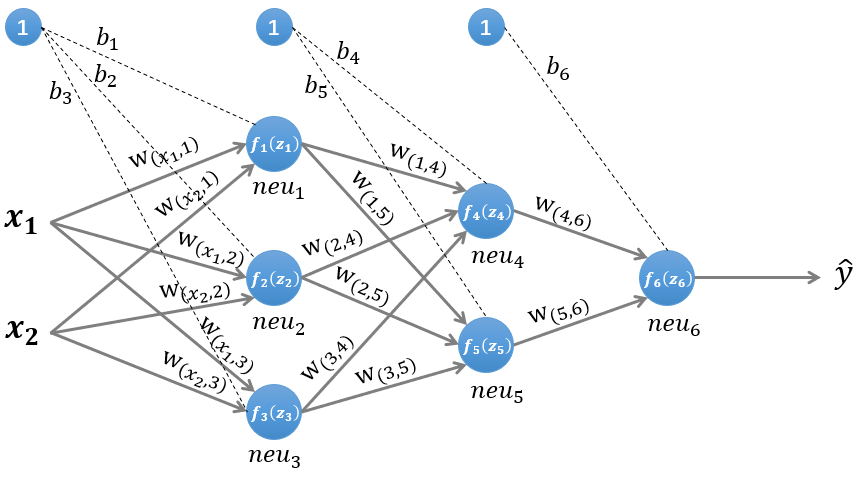
图1所示是一个简单的三层(两个隐藏层,一个输出层)神经网络结构,假设我们使用这个神经网络来解决二分类问题,我们给这个网络一个输入样本 ,通过前向运算得到输出 。输出值 的值域为 ,例如 的值越接近0,代表该样本是“0”类的可能性越大,反之是“1”类的可能性大。 1.1前向传播的计算 为了便于理解后续的内容,我们需要先搞清楚前向传播的计算过程,以图1所示的内容为例: 输入的样本为: a → = ( x 1 , x 2 ) \overrightarrow{a}=(x_ {1} , x_ {2} ) a =(x1,x2) 第一层网络的参数为: W ( 1 ) = [ w ( x 1 , 1 ) , w ( x 2 , 1 ) w ( x 1 , 2 ) , w ( x 2 , 2 ) w ( x 1 , 3 ) , w ( x 2 , 3 ) ] , b ( 1 ) = [ b 1 , b 2 , b 3 ] W^{(1)}=\left[\begin{array}{l}w_{\left(x_{1}, 1\right)}, w_{\left(x_{2}, 1\right)} \\ w_{\left(x_{1}, 2\right)}, w_{\left(x_{2}, 2\right)} \\ w_{\left(x_{1}, 3\right)}, w_{\left(x_{2}, 3\right)}\end{array}\right], \quad b^{(1)}=\left[b_{1}, b_{2}, b_{3}\right] W(1)=⎣⎡w(x1,1),w(x2,1)w(x1,2),w(x2,2)w(x1,3),w(x2,3)⎦⎤,b(1)=[b1,b2,b3] 第二层网络的参数为: W ( 2 ) = [ w ( 1 , 4 ) , w ( 2 , 4 ) , w ( 3 , 4 ) w ( 1 , 5 ) , w ( 2 , 5 ) , w ( 3 , 5 ) ] , b ( 2 ) = [ b 4 , b 5 ] W^{(2)}=\left[\begin{array}{l}w_{(1,4)}, w_{(2,4)}, w_{(3,4)} \\ w_{(1,5)}, w_{(2,5)}, w_{(3,5)}\end{array}\right], \quad b^{(2)}=\left[b_{4}, b_{5}\right] W(2)=[w(1,4),w(2,4),w(3,4)w(1,5),w(2,5),w(3,5)],b(2)=[b4,b5] 第三层网络的参数为: W 3 = [ w ( 4 , 6 ) , w ( 5 , 6 ) ] , b ( 3 ) = [ b 6 ] W^{3}=\left[w_{(4,6)}, w_{(5,6)}\right], \quad b^{(3)}=\left[b_{6}\right] W3=[w(4,6),w(5,6)],b(3)=[b6] 1.1.1 第一层隐藏层的计算
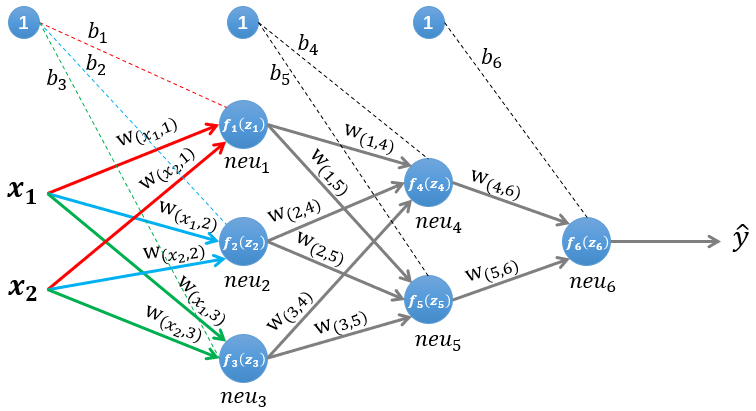
第一层有三个神经元: n e u 1 neu_1 neu1, n e u 2 neu_2 neu2, n e u 3 neu_3 neu3。该层的输入为: Z ( 1 ) = W ( 1 ) ∗ ( a ⃗ ) T + ( b ( 1 ) ) T Z^{(1)}=W^{(1)} *(\vec{a})^{T}+\left(b^{(1)}\right)^{T} Z(1)=W(1)∗(a )T+(b(1))T 以 n e u 1 neu_1 neu1神经元为例,则其输入为: z 1 = w ( x 1 , 1 ) ∗ x 1 + w ( x 2 , 1 ) ∗ x 2 + b 1 z_{1}=w_{\left(x_{1}, 1\right)} * x_{1}+w_{\left(x_{2}, 1\right)} * x_{2}+b_{1} z1=w(x1,1)∗x1+w(x2,1)∗x2+b1 同理有: z 2 = w ( x 1 , 2 ) ∗ x 1 + w ( x 2 , 2 ) ∗ x 2 + b 2 z 3 = w ( x 1 , 3 ) ∗ x 1 + w ( x 2 , 3 ) ∗ x 2 + b 3 \begin{aligned} &z_{2}=w_{\left(x_{1}, 2\right)} * x_{1}+w_{\left(x_{2}, 2\right)} * x_{2}+b_{2} \\ &z_{3}=w_{\left(x_{1}, 3\right)} * x_{1}+w_{\left(x_{2}, 3\right)} * x_{2}+b_{3} \end{aligned} z2=w(x1,2)∗x1+w(x2,2)∗x2+b2z3=w(x1,3)∗x1+w(x2,3)∗x2+b3 假设我们选择函数 f ( x ) f(x) f(x) 作为该层的激活函数 ( 图 1 中的激活函数都际了一个下标,一般情况下,同一层的激活函数都是一样的,不同层可以选择不同的激活函数),那么该层的输出为: f 1 ( z 1 ) , f 2 ( z 2 ) f_{1}(z_{1}), f_{2}\left(z_{2}\right) f1(z1),f2(z2) 和 f 3 ( z 3 ) f_{3}\left(z_{3}\right) f3(z3) 1.1.2 第二层隐藏层的计算
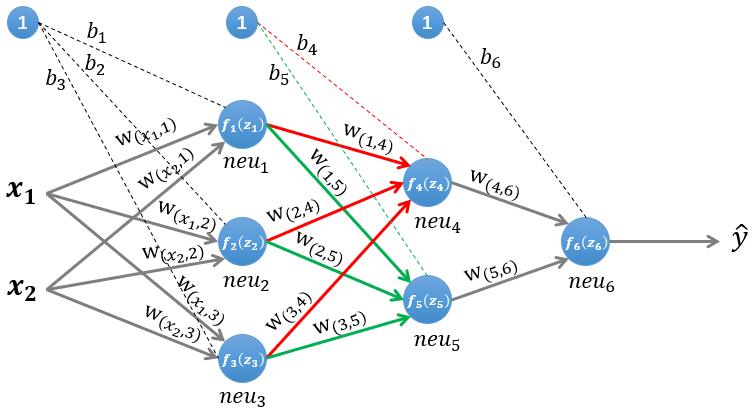
第二层隐藏层有两个神经元: n e u 4 neu_{4} neu4 和 n e u 5 neu_{5} neu5 。 该层的输入为: z ( 2 ) = W ( 2 ) ∗ [ z 1 , z 2 , z 3 ] T + ( b ( 2 ) ) T z^{(2)}=W^{(2)} *\left[z_{1}, z_{2}, z_{3}\right]^{T}+\left(b^{(2)}\right)^{T} z(2)=W(2)∗[z1,z2,z3]T+(b(2))T 即第二层的输入是第一层的输出乘以第二层的权重, 再加上第二层的偏置。因此得到 n e u 4 n e u_{4} neu4 和 n e u 5 n e u_{5} neu5 的输入分别为: z 4 = w ( 1 , 4 ) ∗ z 1 + w ( 2 , 4 ) ∗ z 2 + w ( 3 , 4 ) ∗ z 3 + b 4 z 5 = w ( 1 , 5 ) ∗ z 1 + w ( 2 , 5 ) ∗ z 2 + w ( 3 , 5 ) ∗ z 3 + b 5 \begin{aligned} &z_{4}=w_{(1,4)} * z_{1}+w_{(2,4)} * z_{2}+w_{(3,4)} * z_{3}+b_{4} \\ &z_{5}=w_{(1,5)} * z_{1}+w_{(2,5)} * z_{2}+w_{(3,5)} * z_{3}+b_{5} \end{aligned} z4=w(1,4)∗z1+w(2,4)∗z2+w(3,4)∗z3+b4z5=w(1,5)∗z1+w(2,5)∗z2+w(3,5)∗z3+b5 该层的输出分别为: f 4 ( z 4 ) f_{4}\left(z_{4}\right) f4(z4) 和 f 5 ( z 5 ) f_{5}(z_{5}) f5(z5)。 1.1.3 输出层的计算
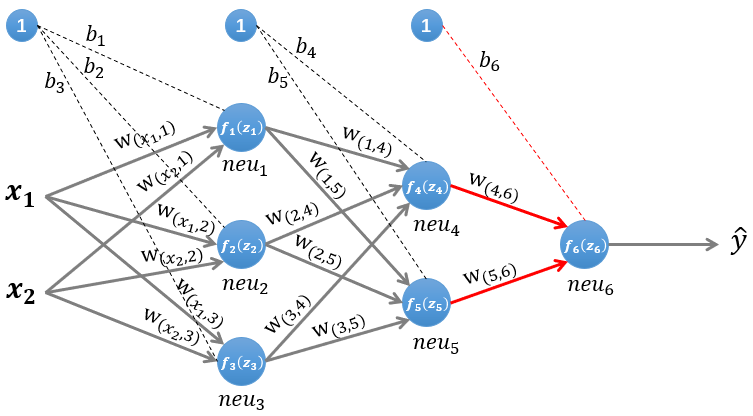
输出层只有一个神经元: n e u 6 neu_6 neu6。该层的输入为: z ( 3 ) = W ( 3 ) ∗ [ z 4 , z 5 ] T + ( b ( 3 ) ) T z^{(3)}=W^{(3)} *\left[z_{4}, z_{5}\right]^{T}+\left(b^{(3)}\right)^{T} z(3)=W(3)∗[z4,z5]T+(b(3))T 即: z 6 = w ( 4 , 6 ) ∗ z 4 + w ( 5 , 6 ) ∗ z 5 + b 6 z_{6}=w_{(4,6)} * z_{4}+w_{(5,6)} * z_{5}+b_{6} z6=w(4,6)∗z4+w(5,6)∗z5+b6 因为该网络要解决的是一个二分类问题,所以输出层的激活函数也可以使用一个 Sigmoid 型函数,神经网络最后的输出为: f 6 ( z 6 ) f_{6}\left(z_{6}\right) f6(z6) 。 1.2 反向传播的计算在 1.1 节里,我们已经了解了数据沿着神经网络前向传播的过程,这一节我们来介绍更重要的反向传播的计算过程。假设我们使用随机梯度下降的方式来学习神经网络的参数,损失函数定义为 L ( y , y ^ ) {L}({y}, \hat{{y}}) L(y,y^),其中y是该样本的真实类标。使用梯度下降进行参数的学习,我们必须计算出损失函数关于神经网络中各层参数(权重 w {w} w 和偏置 b b b) 的偏导数。
假设我们要对第k层隐藏层的参数 W ( k ) W^{(k)} W(k) 和 b ( k ) b^{(k)} b(k) 求偏导数, 即求 ∂ L ( y , y ^ ) ∂ W ( k ) \frac{\partial {L}({y}, \hat{y})}{\partial W^{(k)}} ∂W(k)∂L(y,y^) 和 ∂ L ( y , y ^ ) ∂ b ( k ) \frac{\partial {L}({y}, \hat{y})}{\partial b^{(k)}} ∂b(k)∂L(y,y^) 。假设 Z ( k ) Z^{(k)} Z(k) 代表第 k k k 层神经元的输入,即 z ( k ) = W ( k ) ∗ n ( k − 1 ) + b ( k ) z^{(k)}=W^{(k)} * n^{(k-1)}+b^{(k)} z(k)=W(k)∗n(k−1)+b(k),其中 n ( k − 1 ) n^{(k-1)} n(k−1) 为前一层神经元的输出,则根据链式法则有: ∂ L ( y , y ^ ) ∂ W ( k ) = ∂ L ( y , y ^ ) ∂ z ( k ) ∗ ∂ z ( k ) ∂ W ( k ) ∂ L ( y , y ^ ) ∂ b ( k ) = ∂ L ( y , y ^ ) ∂ z ( k ) ∗ ∂ z ( k ) ∂ b ( k ) \begin{aligned} &\frac{\partial {L}({y}, \hat{{y}})}{\partial W^{(k)}}=\frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k)}} * \frac{\partial z^{(k)}}{\partial W^{(k)}} \\ &\frac{\partial {L}({y}, \hat{{y}})}{\partial b^{(k)}}=\frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k)}} * \frac{\partial z^{(k)}}{\partial b^{(k)}} \end{aligned} ∂W(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂W(k)∂z(k)∂b(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂b(k)∂z(k) 因此,我们只需要计算偏导数 ∂ L ( y , y ^ ) ∂ z ( k ) 、 ∂ z ( k ) ∂ W ( k ) \frac{\partial {L}({y}, \hat{y})}{\partial z^{(k)}} 、 \frac{\partial z^{(k)}}{\partial W^{(k)}} ∂z(k)∂L(y,y^)、∂W(k)∂z(k) 和 ∂ z ( k ) ∂ b ( k ) \frac{\partial z^{(k)}}{\partial b^{(k)}} ∂b(k)∂z(k)。 1.2.1 计算偏导数 ∂ z ( k ) ∂ W ( k ) \frac{\partial z^{(k)}}{\partial W^{(k)}} ∂W(k)∂z(k)前面说过,第 k k k层神经元的输入为: z ( k ) = W ( k ) ∗ n ( k − 1 ) + b ( k ) z^{(k)}=W^{(k)} * n^{(k-1)}+b^{(k)} z(k)=W(k)∗n(k−1)+b(k),因此可以得到: ∂ z ( k ) ∂ W ( k ) = [ ∂ ( W 1 : ( k ) ∗ n ( k − 1 ) + b ( k ) ) ∂ W ( k ) ⋮ ∂ ( W m : ( k ) ∗ n ( k − 1 ) + b ( k ) ) ∂ W ( k ) ] ⟹ 初 等 变 换 ( n k − 1 ) T \frac{\partial z^{(k)}}{\partial W^{(k)}}=\left[\begin{array}{c} \frac{\partial\left(W_{1:}^{(k)} * n^{(k-1)}+b^{(k)}\right)}{\partial W^{(k)}} \\ \vdots \\ \frac{\partial\left(W_{m:}^{(k)} * n^{(k-1)}+b^{(k)}\right)}{\partial W^{(k)}} \end{array}\right] \stackrel{初等变换}\Longrightarrow{{(n^{k-1})}^{T}} ∂W(k)∂z(k)=⎣⎢⎢⎢⎡∂W(k)∂(W1:(k)∗n(k−1)+b(k))⋮∂W(k)∂(Wm:(k)∗n(k−1)+b(k))⎦⎥⎥⎥⎤⟹初等变换(nk−1)T 上式中, W m : ( k ) W_{m:}^{(k)} Wm:(k)代表第k层神经元的权重矩阵 W ( k ) W^{(k)} W(k)的第m行, W m n ( k ) W_{m n}{ }^{(k)} Wmn(k)代表第 k k k层神经元的权重矩阵 W ( k ) W^{(k)} W(k)的第m行中的第n列。 我们以1.1节中的简单神经网络为例,假设我们要计算第一层隐藏层的神经元关于权重矩阵的导数,则有: ∂ z ( 1 ) ∂ W ( 1 ) = ( x 1 , x 2 ) T = ( x 1 x 2 ) \frac{\partial z^{(1)}}{\partial W^{(1)}}=\left(x_{1}, x_{2}\right)^{T}=\left(\begin{array}{l}{x_{1}}\\{x_{2}}\end{array}\right) ∂W(1)∂z(1)=(x1,x2)T=(x1x2) 1.2.2 计算偏导数 ∂ z ( k ) ∂ b ( k ) \frac{\partial z^{(k)}}{\partial b^{(k)}} ∂b(k)∂z(k)因为偏置 b b b 是一个常数项,因此偏导数的计算也很简单: ∂ z ( k ) ∂ b ( k ) = [ ∂ ( W 1 : ( k ) ∗ n ( k − 1 ) + b 1 ) ∂ b 1 ⋯ ∂ ( W 1 : ( k ) ∗ n ( k − 1 ) + b 1 ) ∂ b m ⋮ ⋯ ⋮ ∂ ( W m : ( k ) ∗ n ( k − 1 ) + b m ) ∂ b 1 ⋯ ∂ ( W m : ( k ) ∗ n ( k − 1 ) + b m ) ∂ b m ] \frac{\partial z^{(k)}}{\partial b^{(k)}}=\left[\begin{array}{ccc} \frac{\partial\left(W_{1:}{ }^{(k)} * n^{(k-1)}+b_{1}\right)}{\partial b_{1}} & \cdots & \frac{\partial\left(W_{1:}{ }^{(k)} * n^{(k-1)}+b_{1}\right)}{\partial b_{m}} \\ \vdots & \cdots & \vdots \\ \frac{\partial\left(W_{m:}^{(k)} * n^{(k-1)}+b_{m}\right)}{\partial b_{1}} & \cdots & \frac{\partial\left(W_{m:}{ }^{(k)} * n^{(k-1)}+b_{m}\right)}{\partial b_{m}} \end{array}\right] ∂b(k)∂z(k)=⎣⎢⎢⎢⎡∂b1∂(W1:(k)∗n(k−1)+b1)⋮∂b1∂(Wm:(k)∗n(k−1)+bm)⋯⋯⋯∂bm∂(W1:(k)∗n(k−1)+b1)⋮∂bm∂(Wm:(k)∗n(k−1)+bm)⎦⎥⎥⎥⎤ 依然以第一层隐藏层的神经元为例,则有: ∂ z ( 1 ) ∂ b ( 1 ) = [ 1 0 0 0 1 0 0 0 1 ] \frac{\partial z^{(1)}}{\partial b^{(1)}}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] ∂b(1)∂z(1)=⎣⎡100010001⎦⎤ 1.2.3 计算偏导数 ∂ L ( y , y ^ ) ∂ z ( k ) \frac{\partial {L}({y}, \hat{y})}{\partial z^{(k)}} ∂z(k)∂L(y,y^)偏导数 ∂ L ( y , y ^ ) ∂ z ( k ) \frac{\partial {L}(\mathbf{y}, \hat{y})}{\partial z^{(k)}} ∂z(k)∂L(y,y^) 又称为误差项 (error term,也称为“灵敏度”),一般用 δ \delta δ 表示,例如 δ ( 1 ) = ∂ L ( y , y ^ ) ∂ z ( 1 ) \boldsymbol{\delta}^{(1)}=\frac{\partial {L}({y}, \hat{y})}{\partial z^{(1)}} δ(1)=∂z(1)∂L(y,y^) 是第一层神经元的误差项,其值的大小代表了第一层神经元对于最终总误差的影响大小。 根据第一节的前向计算,我们知道第 k + 1 k+\mathbf{1} k+1 层的输入与第 k k k 层的输出之间的关系为: z ( k + 1 ) = W ( k + 1 ) ∗ n ( k ) + b k + 1 z^{(k+1)}=W^{(k+1)} * n^{(k)}+b^{k+1} z(k+1)=W(k+1)∗n(k)+bk+1 又因为 n ( k ) = f k ( z ( k ) ) n^{(k)}=\boldsymbol{f}_{\boldsymbol{k}}\left(\boldsymbol{z}^{(\boldsymbol{k})}\right) n(k)=fk(z(k)),根据链式法则,我们可以得到 δ ( k ) \boldsymbol{\delta}^{(\boldsymbol{k})} δ(k) 为: δ ( k ) = ∂ L ( y , y ^ ) ∂ z ( k ) = ∂ n ( k ) ∂ z ( k ) ∗ ∂ z ( k + 1 ) ∂ n ( k ) ∗ ∂ L ( y , y ^ ) ∂ z ( k + 1 ) = ∂ n ( k ) ∂ z ( k ) ∗ ∂ z ( k + 1 ) ∂ n ( k ) ∗ δ ( k + 1 ) = f k ′ ( z ( k ) ) ∗ ( ( W ( k + 1 ) ) T ∗ δ ( k + 1 ) ) \begin{aligned} \delta^{(k)} &=\frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k)}} \\ &=\frac{\partial n^{(k)}}{\partial z^{(k)}} * \frac{\partial z^{(k+1)}}{\partial n^{(k)}} * \frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k+1)}}\\ &=\frac{\partial n^{(k)}}{\partial z^{(k)}} * \frac{\partial z^{(k+1)}}{\partial n^{(k)}} * \delta^{(k+1)} \\ &=f_{k}^{\prime}\left(z^{(k)}\right) *\left(\left(W^{(k+1)}\right)^{T} * \delta^{(k+1)}\right) \end{aligned} δ(k)=∂z(k)∂L(y,y^)=∂z(k)∂n(k)∗∂n(k)∂z(k+1)∗∂z(k+1)∂L(y,y^)=∂z(k)∂n(k)∗∂n(k)∂z(k+1)∗δ(k+1)=fk′(z(k))∗((W(k+1))T∗δ(k+1)) 由上式我们可以看到,第 k k k 层神经元的误差项 δ ( k ) \boldsymbol{\delta}^{(\boldsymbol{k})} δ(k) 是由第 k + 1 k+1 k+1 层的误差项乘以第 k + 1 {k}+{1} k+1 层的权重,再乘以第 k {k} k 层激活函数的导数(梯度)得到的。这就是误差的反向传播。 现在我们已经计算出了偏导数 ∂ L ( y , y ^ ) ∂ z ( k ) , ∂ z ( k ) ∂ W ( k ) \frac{\partial {L}(y, \hat{y})}{\partial z^{(k)}}, \frac{\partial z^{(k)}}{\partial W^{(k)}} ∂z(k)∂L(y,y^),∂W(k)∂z(k) 和 ∂ z ( k ) ∂ b ( k ) \frac{\partial z^{(k)}}{\partial b^{(k)}} ∂b(k)∂z(k), 则 ∂ L ( y , y ^ ) ∂ W ( k ) \frac{\partial {L}({y}, \hat{y})}{\partial W^{(k)}} ∂W(k)∂L(y,y^) 和 ∂ L ( y , y ^ ) ∂ b ( k ) \frac{\partial {L}(y, \hat{y})}{\partial b^{(k)}} ∂b(k)∂L(y,y^) 可分别表示为: ∂ L ( y , y ^ ) ∂ W ( k ) = ∂ L ( y , y ^ ) ∂ z ( k ) ∗ ∂ z ( k ) ∂ W ( k ) = δ ( k ) ∗ ( n ( k − 1 ) ) T ∂ L ( y , y ^ ) ∂ b ( k ) = ∂ L ( y , y ^ ) ∂ z ( k ) ∗ ∂ z ( k ) ∂ b ( k ) = δ ( k ) \begin{aligned} &\frac{\partial {L}({y}, \hat{{y}})}{\partial W^{(k)}}=\frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k)}} * \frac{\partial z^{(k)}}{\partial W^{(k)}}=\delta^{(k)} *\left(n^{(k-1)}\right)^{T} \\ &\frac{\partial {L}({y}, \hat{{y}})}{\partial b^{(k)}}=\frac{\partial {L}({y}, \hat{{y}})}{\partial z^{(k)}} * \frac{\partial z^{(k)}}{\partial b^{(k)}}=\delta^{(k)} \end{aligned} ∂W(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂W(k)∂z(k)=δ(k)∗(n(k−1))T∂b(k)∂L(y,y^)=∂z(k)∂L(y,y^)∗∂b(k)∂z(k)=δ(k) 单纯的公式推导看起来有些枯燥,下面我们将实际的数据带入图1所示的神经网络中,完整的计算一遍。 2. 图解BP算法
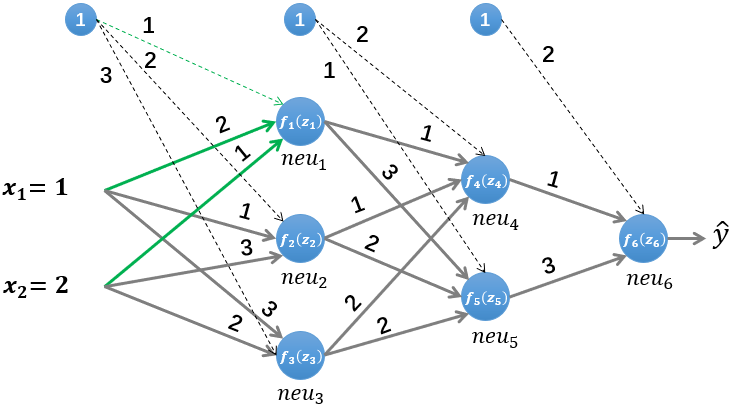
我们依然使用如图5所示的简单的神经网络,其中所有参数的初始值如下: 输入的样本为(假设其真实类标为“1”): a → = ( x 1 , x 2 ) = ( 1 , 2 ) \overrightarrow{{a}}=\left(x_{1}, x_{2}\right)=(1,2) a =(x1,x2)=(1,2) 第一层网络的参数为: W ( 1 ) = [ w ( x 1 , 1 ) , w ( x 2 , 1 ) w ( x 1 , 2 ) , w ( x 2 , 2 ) w ( x 1 , 3 ) , w ( x 2 , 3 ) ] = [ 2 1 1 3 3 2 ] , b ( 1 ) = [ b 1 , b 2 , b 3 ] T = [ 1 , 2 , 3 ] T W^{(1)}=\left[\begin{array}{l} w_{\left(x_{1}, 1\right)}, w_{\left(x_{2}, 1\right)} \\ w_{\left(x_{1}, 2\right)}, w_{\left(x_{2}, 2\right)} \\ w_{\left(x_{1}, 3\right)}, w_{\left(x_{2}, 3\right)} \end{array}\right]=\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right], \quad b^{(1)}=\left[b_{1}, b_{2}, b_{3}\right]^{T}=[1,2,3]^{T} W(1)=⎣⎡w(x1,1),w(x2,1)w(x1,2),w(x2,2)w(x1,3),w(x2,3)⎦⎤=⎣⎡213132⎦⎤,b(1)=[b1,b2,b3]T=[1,2,3]T 第二层网络的参数为: W ( 2 ) = [ w ( 1 , 4 ) , w ( 2 , 4 ) , w ( 3 , 4 ) w ( 1 , 5 ) , w ( 2 , 5 ) , w ( 3 , 5 ) ] = [ 1 1 2 3 2 2 ] , b ( 2 ) = [ b 4 , b 5 ] T = [ 2 , 1 ] T W^{(2)}=\left[\begin{array}{l} w_{(1,4)}, w_{(2,4)}, w_{(3,4)} \\ w_{(1,5)}, w_{(2,5)}, w_{(3,5)} \end{array}\right]=\left[\begin{array}{lll} 1 & 1 & 2 \\ 3 & 2 & 2 \end{array}\right], \quad b^{(2)}=\left[b_{4}, b_{5}\right]^{T}=[2,1]^{T} W(2)=[w(1,4),w(2,4),w(3,4)w(1,5),w(2,5),w(3,5)]=[131222],b(2)=[b4,b5]T=[2,1]T 第三层网络的参数为: W 3 = [ w ( 4 , 6 ) , w ( 5 , 6 ) ] = [ 1 , 3 ] , b ( 3 ) = [ b 6 ] = [ 2 ] W^{3}=\left[w_{(4,6)}, w_{(5,6)}\right]=[1,3], \quad b^{(3)}=\left[b_{6}\right]=[2] W3=[w(4,6),w(5,6)]=[1,3],b(3)=[b6]=[2] 假设所有的激活函数均为 Logistic 函数: f ( k ) ( x ) = 1 1 + e − x f^{(k)}(x)=\frac{1}{1+e^{-x}} f(k)(x)=1+e−x1 。使用均方误差函数作为损失函数: L ( y , y ^ ) = E ( y − y ^ ) 2 {L}({y}, \hat{{y}})={E}({y}-\hat{{y}})^{2} L(y,y^)=E(y−y^)2 为了方便求导,我们将损失函数简化为: L ( y , y ^ ) = 1 2 ∑ ( y − y ^ ) 2 。 {L}({y}, \hat{{y}})=\frac{1}{2} \sum({y}-\hat{{y}})^{2} 。 L(y,y^)=21∑(y−y^)2。 2.1 前向传播我们首先初始化神经网络的参数,计算第一层神经元:
f 1 ( z 1 ) = 1 1 + e − z 1 = 0.993307149075715 f_{1}\left(z_{1}\right)=\frac{1}{1+e^{-z_{1}}}=0.993307149075715 f1(z1)=1+e−z11=0.993307149075715 上图中我们计算出了第一层隐藏层的第一个神经元的输入 z 1 z_{1} z1 和输出 f 1 ( z 1 ) f_{1}\left(z_{1}\right) f1(z1),同理可以计算第二 个和第三个神经元的输入和输出:
f 2 ( z 2 ) = 1 1 + e − z 2 = 0.999876605424014 f_{2}\left(z_{2}\right)=\frac{1}{1+e^{-z_{2}}}=0.999876605424014 f2(z2)=1+e−z21=0.999876605424014 z 3 = w ( x 1 , 3 ) ∗ x 1 + w ( x 2 , 3 ) ∗ x 2 + b 3 = 3 ∗ 1 + 2 ∗ 2 + 3 = 10 \begin{aligned} z_{3} &=w_{\left(x_{1}, 3\right)} * x_{1}+w_{\left(x_{2}, 3\right)} * x_{2}+b_{3} \\ &=3 * 1+2 * 2+3=10 \end{aligned} z3=w(x1,3)∗x1+w(x2,3)∗x2+b3=3∗1+2∗2+3=10 f 3 ( z 3 ) = 1 1 + e − z 3 = 0.999954602131298 \begin{aligned} f_{3}\left(z_{3}\right)=& \frac{1}{1+e^{-z_{3}}}=0.999954602131298 \end{aligned} f3(z3)=1+e−z31=0.999954602131298 接下来是第二层隐藏层的计算,首先我们计算第二层的第一个神经元的输入 z 4 z_{4} z4 和输出 f 4 ( z 4 ) f_{4}\left(z_{4}\right) f4(z4) :
同样方法可以计算该层的第二个神经元的输入 z 5 z_{5} z5 和输出 f 5 ( z 5 ) f_{5}\left(z_{5}\right) f5(z5) :
f 5 ( z 5 ) = 1 1 + e − z 5 = 0.999874045072167 f_{5}\left(z_{5}\right)=\frac{1}{1+e^{-z_{5}}}=0.999874045072167 f5(z5)=1+e−z51=0.999874045072167 最后计算输出层的输入 z 6 z_{6} z6 和输出 f 6 ( z 6 ) f_{6}\left(z_{6}\right) f6(z6) :
首先计算输出层的误差项 δ 3 \delta_{3} δ3,我们的误差函数为 L ( y , y ^ ) = 1 2 ∑ ( y − y ^ ) 2 {L}({y}, \hat{{y}})=\frac{1}{2} \sum({y}-\hat{{y}})^{2} L(y,y^)=21∑(y−y^)2,由于该样本的类标为“1",而预测值为 0.997520293823002 0.997520293823002 0.997520293823002,因此误差为 0.002479706176998 0.002479706176998 0.002479706176998,输出层的误差项为: δ 3 = ∂ L ( y , y ^ ) ∂ z ( 3 ) = ∂ L ( y , y ^ ) ∂ n ( 3 ) ∗ ∂ n ( 3 ) ∂ z ( 3 ) = [ − 0.002479706176998 ] ∗ f ( 3 ) ′ ( z 3 ) = [ 0.002473557234274 ] ∗ [ − 0.002479706176998 ] = [ − 0.000006133695153 ] \begin{aligned} \delta_{3}&=\frac{\partial {L}({y}, \hat{y})}{\partial z^{(3)}}=\frac{\partial {L}({y}, \hat{{y}})}{\partial n^{(3)}} * \frac{\partial n^{(3)}}{\partial z^{(3)}}=[-0.002479706176998] * f^{(3)\prime}\left(z^{3}\right) \\ &=[0.002473557234274] *[-0.002479706176998] \\ &=[-0.000006133695153] \end{aligned} δ3=∂z(3)∂L(y,y^)=∂n(3)∂L(y,y^)∗∂z(3)∂n(3)=[−0.002479706176998]∗f(3)′(z3)=[0.002473557234274]∗[−0.002479706176998]=[−0.000006133695153] 接着计算第二层隐藏层的误差项,根据误差项的计算公式有: δ ( 2 ) = ∂ L ( y , y ^ ) ∂ z ( 2 ) = f ( 2 ) ′ ( z ( 2 ) ) ∗ ( ( W ( 3 ) ) T ∗ δ ( 3 ) ) = [ f 4 ′ ( z 4 ) 0 0 f 5 ′ ( z 5 ) ] ∗ ( [ 1 3 ] ∗ [ − 0.000006133695153 ] ) = [ 0.002483519419601 0 0.000125939063189 ] ∗ [ − 0.000006133695153 − 0.000018401085459 ] = [ − 0.000000015233151 − 0.000000002317415 ] \begin{aligned} \delta^{(2)}&=\frac{\partial {L}({y}, \hat{y})}{\partial z^{(2)}}=f^{(2)\prime}\left(z^{(2)}\right) *\left(\left(W^{(3)}\right)^{T} * \delta^{(3)}\right) \\ &=\left[\begin{array}{cc} f_{4}^{\prime}\left(z_{4}\right) & 0 \\ 0 & f_{5}^{\prime}\left(z_{5}\right) \end{array}\right] *\left(\left[\begin{array}{l} 1 \\ 3 \end{array}\right] *[-0.000006133695153]\right) \\ &=\left[\begin{array}{c} 0.002483519419601 \\ 0 & 0.000125939063189 \end{array}\right] *\left[\begin{array}{l} -0.000006133695153 \\ -0.000018401085459 \end{array}\right] \\ &=\left[\begin{array}{c} -0.000000015233151 \\ -0.000000002317415 \end{array}\right] \end{aligned} δ(2)=∂z(2)∂L(y,y^)=f(2)′(z(2))∗((W(3))T∗δ(3))=[f4′(z4)00f5′(z5)]∗([13]∗[−0.000006133695153])=[0.00248351941960100.000125939063189]∗[−0.000006133695153−0.000018401085459]=[−0.000000015233151−0.000000002317415] 最后是计算第一层隐藏层的误差项: δ ( 1 ) = ∂ L ( y , y ^ ) ∂ n ( 1 ) = f ( 1 ) ′ ( n ( 1 ) ) ∗ ( ( W ( 2 ) ) T ∗ δ ( 2 ) ) = [ f 1 ′ ( z 1 ) 0 0 0 f 2 ′ ( z 2 ) 0 0 0 f 3 ′ ( z 3 ) ] = [ 0.006648056670790 0 0 0 0.000123379349765 0 0 0 0.000045395807735 ] ∗ ( [ 1 1 2 3 2 2 ] T ∗ [ − 0.000000015233151 − 0.000000002317415 ] ) = [ − 0.000000000147490 − 0.000000000002451 − 0.000000000001593 ] \begin{aligned} \delta^{(1)}&=\frac{\partial {L}({y}, \hat{{y}})}{\partial n^{(1)}}=f^{(1)^{\prime}}\left(n^{(1)}\right) *\left(\left(W^{(2)}\right)^{T} * \delta^{(2)}\right) \\ &=\left[\begin{array}{ccc} f_{1}^{\prime}\left(z_{1}\right) & 0 & 0 \\ 0 & f_{2}^{\prime}\left(z_{2}\right) & 0 \\ 0 & 0 & f_{3}^{\prime}\left(z_{3}\right) \end{array}\right] \\ &=\left[\begin{array}{ccc} 0.006648056670790 & 0 & 0 \\ 0 & 0.000123379349765 & 0 \\ 0 & 0 & 0.000045395807735 \end{array}\right] \\ &*\left(\left[\begin{array}{lll} 1 & 1 & 2 \\ 3 & 2 & 2 \end{array}\right]^{T} *\left[\begin{array}{l} -0.000000015233151 \\ -0.000000002317415 \end{array}\right]\right) \\ &=\left[\begin{array}{l} -0.000000000147490 \\ -0.000000000002451 \\ -0.000000000001593 \end{array}\right] \end{aligned} δ(1)=∂n(1)∂L(y,y^)=f(1)′(n(1))∗((W(2))T∗δ(2))=⎣⎡f1′(z1)000f2′(z2)000f3′(z3)⎦⎤=⎣⎡0.0066480566707900000.0001233793497650000.000045395807735⎦⎤∗([131222]T∗[−0.000000015233151−0.000000002317415])=⎣⎡−0.000000000147490−0.000000000002451−0.000000000001593⎦⎤ 2.3 更新参数上一小节中我们已经计算出了每一层的误差项,现在我们要利用每一层的误差项和梯度来更新每一层的参数,权重 W W W和偏置 b b b的更新公式如下: W ( k ) = W ( k ) − α ( δ ( k ) ( n ( k − 1 ) ) T + W ( k ) ) b ( k ) = b ( k ) − α δ ( k ) \begin{gathered} W^{(k)}=W^{(k)}-\alpha\left(\delta^{(k)}\left(n^{(k-1)}\right)^{T}+W^{(k)}\right) \\ b^{(k)}=b^{(k)}-\alpha \delta^{(k)} \end{gathered} W(k)=W(k)−α(δ(k)(n(k−1))T+W(k))b(k)=b(k)−αδ(k) W ( 1 ) = W ( 1 ) − 0.1 ∗ ( δ ( 1 ) ( n ( 0 ) ) T + W ( 1 ) ) = [ 2 1 1 3 3 2 ] − 0.1 ∗ ( [ − 0.000000000147490 − 0.000000000002451 − 0.000000000001593 ] ∗ [ x 1 x 2 ] + [ 2 1 1 3 3 2 ] ) = [ 2 1 1 3 3 2 ] − 0.1 ∗ ( [ − 0.000000000147490 − 0.000000000002451 − 0.000000000001593 ] ∗ [ 1 2 ] + [ 2 1 1 3 3 2 ] ) = [ 2 1 1 3 3 2 ] − 0.1 ∗ [ 1.999999999852510 0.999999999705020 0.999999999997549 2.999999999995098 2.999999999998407 1.999999999996814 ] = [ 1.800000000014749 0.900000000029498 0.900000000000245 2.700000000000490 2.700000000000159 1.800000000000319 ] \begin{aligned} W^{(1)}&=W^{(1)}-0.1 *\left(\delta^{(1)}\left(n^{(0)}\right)^{T}+W^{(1)}\right) \\ &=\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right]-0.1 *\left(\left[\begin{array}{ll} -0.000000000147490 \\ -0.000000000002451 \\ -0.000000000001593 \end{array}\right] *\left[\begin{array}{ll} x_{1} & x_{2} \end{array}\right]+\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right]\right) \\ &=\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right]-0.1 *\left(\left[\begin{array}{ll} -0.000000000147490 \\ -0.000000000002451 \\ -0.000000000001593 \end{array}\right] *\left[\begin{array}{ll} 1 & 2 \end{array}\right]+\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right]\right) \\ &=\left[\begin{array}{ll} 2 & 1 \\ 1 & 3 \\ 3 & 2 \end{array}\right]-0.1 *\left[\begin{array}{ll} 1.999999999852510 & 0.999999999705020 \\ 0.999999999997549 & 2.999999999995098 \\ 2.999999999998407 & 1.999999999996814 \end{array}\right] \\ &=\left[\begin{array}{ll} 1.800000000014749 & 0.900000000029498 \\ 0.900000000000245 & 2.700000000000490 \\ 2.700000000000159 & 1.800000000000319 \end{array}\right] \end{aligned} W(1)=W(1)−0.1∗(δ(1)(n(0))T+W(1))=⎣⎡213132⎦⎤−0.1∗⎝⎛⎣⎡−0.000000000147490−0.000000000002451−0.000000000001593⎦⎤∗[x1x2]+⎣⎡213132⎦⎤⎠⎞=⎣⎡213132⎦⎤−0.1∗⎝⎛⎣⎡−0.000000000147490−0.000000000002451−0.000000000001593⎦⎤∗[12]+⎣⎡213132⎦⎤⎠⎞=⎣⎡213132⎦⎤−0.1∗⎣⎡1.9999999998525100.9999999999975492.9999999999984070.9999999997050202.9999999999950981.999999999996814⎦⎤=⎣⎡1.8000000000147490.9000000000002452.7000000000001590.9000000000294982.7000000000004901.800000000000319⎦⎤ b ( 1 ) = b ( 1 ) − α δ ( 1 ) = [ 1 , 2 , 3 ] T − 0.1 ∗ [ − 0.000000000147490 − 0.000000000002451 − 0.000000000001593 ] = [ 0.999999999985251 1.999999999999755 2.999999999999841 ] \begin{aligned} b^{(1)}&=b^{(1)}-\alpha \delta^{(1)}\\ &=[1,2,3]^{T}-0.1 *\left[\begin{array}{l}-0.000000000147490 \\ -0.000000000002451 \\ -0.000000000001593\end{array}\right]\\ &=\left[\begin{array}{l}0.999999999985251 \\ 1.999999999999755 \\ 2.999999999999841\end{array}\right]\\ \end{aligned} b(1)=b(1)−αδ(1)=[1,2,3]T−0.1∗⎣⎡−0.000000000147490−0.000000000002451−0.000000000001593⎦⎤=⎣⎡0.9999999999852511.9999999999997552.999999999999841⎦⎤ 通常权重 W W W的更新会加上一个正则化项来避免过拟合,这里为了简化计算,我们省去了正则化项。上式中的 是学习率,我们设其值为 0.1 0.1 0.1。参数更新的计算相对简单,每一层的计算方式都相同,因此本文仅演示第一层隐藏层的参数更新: 3. 小结至此,我们已经完整介绍了BP算法的原理,并使用具体的数值做了计算。在下篇中,我们将带着读者一起亲手实现一个BP神经网络(不适用任何第三方的深度学习框架),敬请期待!有任何疑问,欢迎加入我们一起交流! 本篇文章出自http://www.tensorflownews.com,对深度学习感兴趣,热爱Tensorflow的小伙伴,欢迎关注我们的网站! |
【本文地址】
今日新闻 |
推荐新闻 |

 z
1
=
w
(
x
1
,
1
)
∗
x
1
+
w
(
x
2
,
1
)
∗
x
2
+
b
1
=
2
∗
1
+
1
∗
2
+
1
=
5
\begin{aligned} z_{1} &=w_{\left(x_{1}, 1\right)} * x_{1}+w_{\left(x_{2}, 1\right)} * x_{2}+b_{1} \\ &=2 * 1+1 * 2+1 \\ &=5 \\ \end{aligned}
z1=w(x1,1)∗x1+w(x2,1)∗x2+b1=2∗1+1∗2+1=5
z
1
=
w
(
x
1
,
1
)
∗
x
1
+
w
(
x
2
,
1
)
∗
x
2
+
b
1
=
2
∗
1
+
1
∗
2
+
1
=
5
\begin{aligned} z_{1} &=w_{\left(x_{1}, 1\right)} * x_{1}+w_{\left(x_{2}, 1\right)} * x_{2}+b_{1} \\ &=2 * 1+1 * 2+1 \\ &=5 \\ \end{aligned}
z1=w(x1,1)∗x1+w(x2,1)∗x2+b1=2∗1+1∗2+1=5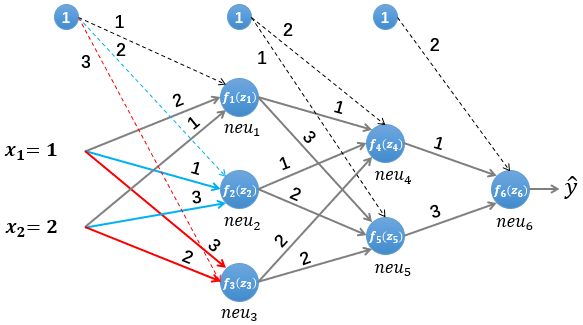 z
2
=
w
(
x
1
,
2
)
∗
x
1
+
w
(
x
2
,
2
)
∗
x
2
+
b
2
=
1
∗
1
+
3
∗
2
+
2
=
9
\begin{aligned} z_{2} &=w_{\left(x_{1}, 2\right)} * x_{1}+w_{\left(x_{2}, 2\right)} * x_{2}+b_{2} \\ &=1 * 1+3 * 2+2 \\ &=9 \end{aligned}
z2=w(x1,2)∗x1+w(x2,2)∗x2+b2=1∗1+3∗2+2=9
z
2
=
w
(
x
1
,
2
)
∗
x
1
+
w
(
x
2
,
2
)
∗
x
2
+
b
2
=
1
∗
1
+
3
∗
2
+
2
=
9
\begin{aligned} z_{2} &=w_{\left(x_{1}, 2\right)} * x_{1}+w_{\left(x_{2}, 2\right)} * x_{2}+b_{2} \\ &=1 * 1+3 * 2+2 \\ &=9 \end{aligned}
z2=w(x1,2)∗x1+w(x2,2)∗x2+b2=1∗1+3∗2+2=9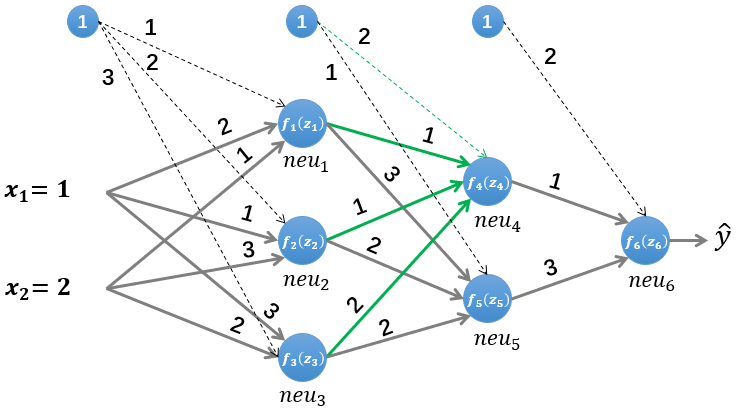 z
4
=
w
(
1
,
4
)
∗
f
1
(
z
1
)
+
w
(
2
,
4
)
∗
f
2
(
z
2
)
+
w
(
3
,
4
)
∗
f
3
(
z
3
)
+
b
4
=
1
∗
0.993307149075715
+
1
∗
0.999876605424014
+
2
∗
0.999954602131298
+
2
=
5.993092958762325
\begin{aligned} z_{4}&=w_{(1,4)} * f_{1}\left(z_{1}\right)+w_{(2,4)} * f_{2}\left(z_{2}\right)+w_{(3,4)} * f_{3}\left(z_{3}\right)+b_{4} \\ &=1 * 0.993307149075715+1 * 0.999876605424014+2 * 0.999954602131298+2 \\ &=5.993092958762325 \end{aligned}
z4=w(1,4)∗f1(z1)+w(2,4)∗f2(z2)+w(3,4)∗f3(z3)+b4=1∗0.993307149075715+1∗0.999876605424014+2∗0.999954602131298+2=5.993092958762325
f
4
(
z
4
)
=
1
1
+
e
−
z
4
=
0.997510281884102
f_{4}\left(z_{4}\right)=\frac{1}{1+e^{-z_{4}}}=0.997510281884102
f4(z4)=1+e−z41=0.997510281884102
z
4
=
w
(
1
,
4
)
∗
f
1
(
z
1
)
+
w
(
2
,
4
)
∗
f
2
(
z
2
)
+
w
(
3
,
4
)
∗
f
3
(
z
3
)
+
b
4
=
1
∗
0.993307149075715
+
1
∗
0.999876605424014
+
2
∗
0.999954602131298
+
2
=
5.993092958762325
\begin{aligned} z_{4}&=w_{(1,4)} * f_{1}\left(z_{1}\right)+w_{(2,4)} * f_{2}\left(z_{2}\right)+w_{(3,4)} * f_{3}\left(z_{3}\right)+b_{4} \\ &=1 * 0.993307149075715+1 * 0.999876605424014+2 * 0.999954602131298+2 \\ &=5.993092958762325 \end{aligned}
z4=w(1,4)∗f1(z1)+w(2,4)∗f2(z2)+w(3,4)∗f3(z3)+b4=1∗0.993307149075715+1∗0.999876605424014+2∗0.999954602131298+2=5.993092958762325
f
4
(
z
4
)
=
1
1
+
e
−
z
4
=
0.997510281884102
f_{4}\left(z_{4}\right)=\frac{1}{1+e^{-z_{4}}}=0.997510281884102
f4(z4)=1+e−z41=0.997510281884102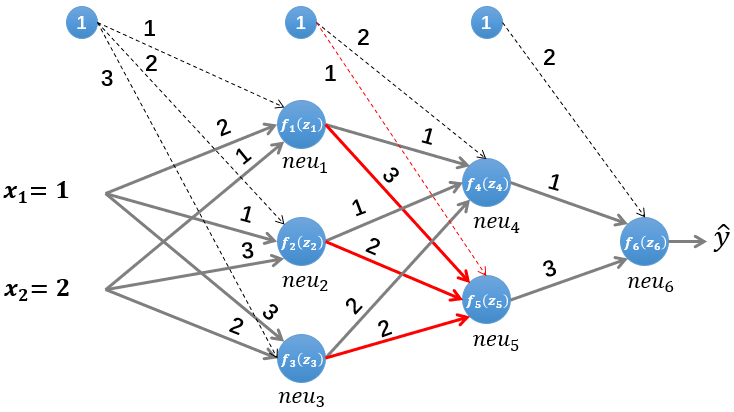 z
5
=
w
(
1
,
5
)
∗
f
1
(
z
1
)
+
w
(
2
,
5
)
∗
f
2
(
z
2
)
+
w
(
3
,
5
)
∗
f
3
(
z
3
)
+
b
5
=
3
∗
0.993307149075715
+
3
∗
0.999876605424014
+
2
∗
0.999954602131298
+
1
=
8.979460467761783
\begin{aligned} z_{5}&=w_{(1,5)} * f_{1}\left(z_{1}\right)+w_{(2,5)} * f_{2}\left(z_{2}\right)+w_{(3,5)} * f_{3}\left(z_{3}\right)+b_{5}\\ &=3 * 0.993307149075715+3 * 0.999876605424014+2 * 0.999954602131298+1 \\ &=8.979460467761783 \end{aligned}
z5=w(1,5)∗f1(z1)+w(2,5)∗f2(z2)+w(3,5)∗f3(z3)+b5=3∗0.993307149075715+3∗0.999876605424014+2∗0.999954602131298+1=8.979460467761783
z
5
=
w
(
1
,
5
)
∗
f
1
(
z
1
)
+
w
(
2
,
5
)
∗
f
2
(
z
2
)
+
w
(
3
,
5
)
∗
f
3
(
z
3
)
+
b
5
=
3
∗
0.993307149075715
+
3
∗
0.999876605424014
+
2
∗
0.999954602131298
+
1
=
8.979460467761783
\begin{aligned} z_{5}&=w_{(1,5)} * f_{1}\left(z_{1}\right)+w_{(2,5)} * f_{2}\left(z_{2}\right)+w_{(3,5)} * f_{3}\left(z_{3}\right)+b_{5}\\ &=3 * 0.993307149075715+3 * 0.999876605424014+2 * 0.999954602131298+1 \\ &=8.979460467761783 \end{aligned}
z5=w(1,5)∗f1(z1)+w(2,5)∗f2(z2)+w(3,5)∗f3(z3)+b5=3∗0.993307149075715+3∗0.999876605424014+2∗0.999954602131298+1=8.979460467761783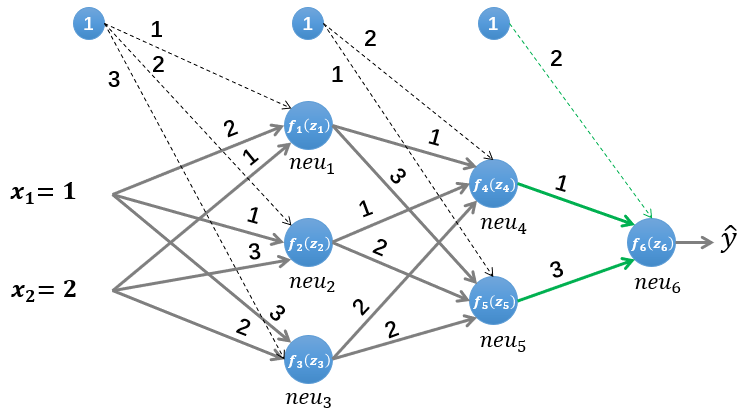 z
4
=
w
(
1
,
4
)
∗
f
1
(
z
1
)
+
w
(
2
,
4
)
∗
f
2
(
z
2
)
+
w
(
3
,
4
)
∗
f
3
(
z
3
)
+
b
4
=
1
∗
0.993307149075715
+
1
∗
0.999876605424014
+
2
∗
0.999954602131298
+
2
=
5.993092958762325
\begin{aligned} z_{4}&=w_{(1,4)} * f_{1}\left(z_{1}\right)+w_{(2,4)} * f_{2}\left(z_{2}\right)+w_{(3,4)} * f_{3}\left(z_{3}\right)+b_{4} \\ &=1 * 0.993307149075715+1 * 0.999876605424014+2 * 0.999954602131298+2 \\ &=5.993092958762325 \end{aligned}
z4=w(1,4)∗f1(z1)+w(2,4)∗f2(z2)+w(3,4)∗f3(z3)+b4=1∗0.993307149075715+1∗0.999876605424014+2∗0.999954602131298+2=5.993092958762325
f
4
(
z
4
)
=
1
1
+
e
−
z
4
=
0.997510281884102
f_{4}\left(z_{4}\right)=\frac{1}{1+e^{-z_{4}}}=0.997510281884102
f4(z4)=1+e−z41=0.997510281884102
z
4
=
w
(
1
,
4
)
∗
f
1
(
z
1
)
+
w
(
2
,
4
)
∗
f
2
(
z
2
)
+
w
(
3
,
4
)
∗
f
3
(
z
3
)
+
b
4
=
1
∗
0.993307149075715
+
1
∗
0.999876605424014
+
2
∗
0.999954602131298
+
2
=
5.993092958762325
\begin{aligned} z_{4}&=w_{(1,4)} * f_{1}\left(z_{1}\right)+w_{(2,4)} * f_{2}\left(z_{2}\right)+w_{(3,4)} * f_{3}\left(z_{3}\right)+b_{4} \\ &=1 * 0.993307149075715+1 * 0.999876605424014+2 * 0.999954602131298+2 \\ &=5.993092958762325 \end{aligned}
z4=w(1,4)∗f1(z1)+w(2,4)∗f2(z2)+w(3,4)∗f3(z3)+b4=1∗0.993307149075715+1∗0.999876605424014+2∗0.999954602131298+2=5.993092958762325
f
4
(
z
4
)
=
1
1
+
e
−
z
4
=
0.997510281884102
f_{4}\left(z_{4}\right)=\frac{1}{1+e^{-z_{4}}}=0.997510281884102
f4(z4)=1+e−z41=0.997510281884102