一文看懂:单颗粒在流体中的受力 |
您所在的位置:网站首页 › 离心力是质量力 › 一文看懂:单颗粒在流体中的受力 |
一文看懂:单颗粒在流体中的受力
|
一、单颗粒在流体中的受力可分为以下三类:
与流体-颗粒相对运动无关的力:惯性力、重力、压力梯度力、浮力
与流体-颗粒相对运动相关、力的方向沿相对运动方向:曳力、附加质量力、Basset力
与流体-颗粒相对运动相关、力的方向垂直于相对运动方向:升力、Magnus力、Saffman力
以上受力的牛顿第二定律表达:所有受力相加为零。
二、逐个描述
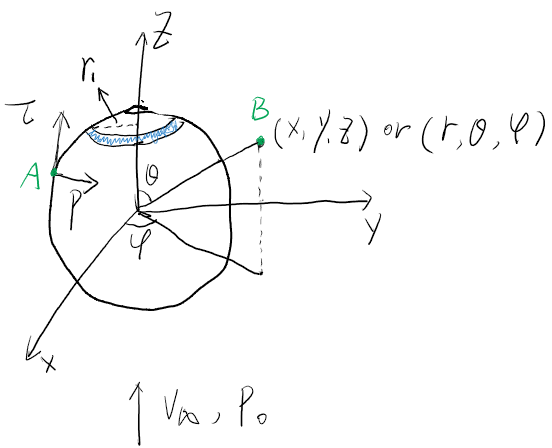
下文中,颗粒直径为\(d\),密度为\(\rho_p\),流体密度为\(\rho_g\),流体动力粘度为\(\mu\),\(u_p,u_g,u_s\)分别表示颗粒速度,流体速度,滑移速度(流体-颗粒) 1. 惯性力当物体加速时,惯性会是物体有保持原有运动状态的倾向,若是以该物体为参照物,看起来仿佛有一股方向相反的力作用在该物体上。 \[F=-\frac{1}{6}\pi d^3 \rho_p \frac{du_p}{dt} \]从表达式可以看出,惯性力为\(ma\),即其他力的合力 2. 曳力又称阻力,是流体与颗粒发生相对运动时所产生的与运动方向相反的力。 \[F=\frac{1}{2}\rho_g u_s^2 A_p C_D=\frac{1}{2}\rho_g u_s^2 \frac{\pi d^2}{4} C_D=\frac{1}{8}\pi d^2 \rho_g u_s^2 C_D \]其中\(C_D\)为阻力系数。如果流动为“爬流”,则\(C_D\)有解析解,即斯托克斯定律。 2.1 低速运动时球体曳力的斯托克斯定律这种“低速”运动还被称为“爬流”,“滞流”,“斯托克斯流”。如图,流体从无穷远处向\(z\)轴正方向流动,来流速度为\(v_{\infty}\),压力\(p_0\) 颗粒表面\(A\)点处的局部面元会受到平行于面元法向的压力以及垂直于面元法向的剪切力即摩擦力。通过计算压力和摩擦力在\(z\)方向分力沿整个颗粒表面的积分,可以得到颗粒在\(z\)方向所受的阻力。在球坐标系中,空间点\(B\)的坐标如图为\((r,\theta,\phi)\)。\(\theta\)为\(B\)点与原点连线和\(z\)轴的夹角,\(\phi\)为\(B\)点在\(xy\)平面投影与\(x\)轴的夹角。
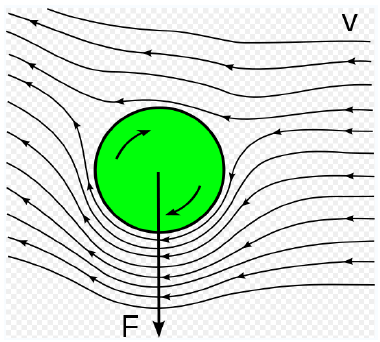
对于爬流,球坐标系下空间中任意一点的压力\(p\)和剪切力为\(\tau\) \[p=p_0-\rho gz - \frac{3}{2}\frac{\mu v_{\infty}}{R}\left(\frac{R}{r}\right)^2cos \theta \]\[\tau_{r\theta}=\frac{3}{2}\frac{\mu v_{\infty}}{R}\left(\frac{R}{r}\right)^4cos \theta \]以上推导过程见《传递过程原理》流函数章节。压力方程中的笛卡尔坐标与球坐标的转化为\(z=rcos\theta\) 将\(p\)和\(\tau\)的\(z\)方向的分力沿整个球面积分。首先计算图中蓝色圆环的面积。设圆环所在的、与\(xy\)平面平行的圆的半径为\(r_1\),球半径为\(R\),圆环与\(z\)轴夹角为\(\theta\),圆环上端与下端之间的夹角为\(d\theta\),对应的弧长为\(dh=Rd\theta\),则圆环(也可以认为是球台)的面积为 \[dS=2\pi r_1 dh=2\pi Rsin\theta Rd\theta=2\pi R^2 sin\theta d\theta \]由\(p\)产生的\(z\)方向分力积分为 \[F_p = \int -pcos\theta dS = \int_0^\pi -pcos\theta 2\pi R^2 sin\theta d\theta \\ = \int_0^\pi (-p_0+\rho_g gRcos\theta +\frac{3}{2}\frac{\mu v_{\infty}}{R}cos\theta) cos\theta 2\pi R^2 sin\theta d\theta \\ = \int_0^\pi (-p_0) cos\theta 2\pi R^2 sin\theta d\theta \\ + \int_0^\pi (\rho_g gRcos\theta) cos\theta 2\pi R^2 sin\theta d\theta \\ + \int_0^\pi (\frac{3}{2}\frac{\mu v_{\infty}}{R}cos\theta) cos\theta 2\pi R^2 sin\theta d\theta \\ =0+\frac{4}{3}\pi R^3 \rho_g g + 2\pi \mu R v_{\infty} \]可见,在静止流体中,颗粒表面压力积分为浮力,即压力梯度力=浮力。 由\(\tau\)产生的\(z\)方向分力积分为 \[F_{\tau}=\int_0^\pi \tau sin\theta 2\pi R^2 sin\theta d\theta=4\pi \mu R v_{\infty} \]因此,颗粒在\(z\)方向受到的流体总的作用力为 \[F=F_p+F_{\tau}=\frac{4}{3}\pi R^3 \rho_g g + 6\pi \mu R v_{\infty} \]其中运动部分产生的阻力为\(6\pi \mu R v_{\infty}=3\pi \mu d v_{\infty}\),阻力系数或曳力系数为 \[C_D=\frac{3\pi \mu d v_{\infty}}{\frac{1}{2}\rho_g v_{\infty}^2 \pi R^2} = \frac{24}{Re} \]其中\(Re=\rho_g v_{\infty} d/\mu\),上式则为斯托克斯定律。其应用范围为爬流。 3. 压力梯度力前面已经提到过,压力梯度力与流体和颗粒之间是否存在相对运动无关,只要把颗粒置于有压力梯度的流场中,则颗粒会受压力梯度引起的力: \[F=V_p \frac{dp}{dx} \]静止流体中,只有重力方向存在压力梯度, \[\frac{dp}{dz}=\rho_g g \]此时压力梯度力=浮力,与前文结果相同。 4. 附加质量力颗粒以相对加速度在流体中作加速运动时,必将带动周围流体加速,因此这种推动颗粒做加速运动的力同时也推动了流体运动,这就好像是颗粒质量变大了一样。颗粒在静止、无粘、不可压缩流体中的变速运动过程经推导可得颗粒表面压力分布为 \[p=p_0+\frac{\rho_g u_p^2}{2}(1-\frac{9}{4}sin^2\theta)-\frac{\rho_g R}{2}cos\theta \frac{du_p}{dt} \]可见,如果颗粒做匀速直线运动,则上式不存在最后一项。对最后一项做球面积分可计算出附加质量力的大小 \[F=-\frac{1}{2}\rho_g V_p \frac{du_p}{dt} \]5. Basset力由于流体有粘性,当颗粒有相对加速度时,颗粒周围的流场不能马上达到稳定。因此,流体对颗粒的作用力不仅依赖于当时颗粒的相对速度(曳力)、当时的相对加速度(附加质量力),还依赖于这之前加速度的历史。 6. Magnus升力若在流场中存在速度梯度,该梯度会引起颗粒旋转。这时,因为速度大的一侧压力小,速度小的一侧压力大,这样产生的压差力将推动球体向速度大的一侧移动,这种推动力为Magnus力。足球比赛中的“香蕉球”和此力有关。
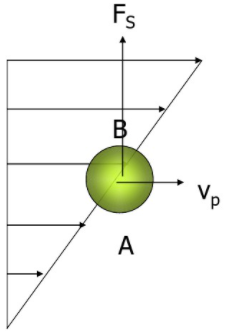
该力和颗粒旋转有关,颗粒旋转角速度为\(\omega\),则颗粒在运动流体中的Magnus力为 \[F=\frac{3}{4}V_p \rho_g \omega u_s \]7. Saffman升力当颗粒处于有速度梯度的流场中,即使颗粒没有旋转,也会受横向升力。
通常在壁面处需要考虑该力,因为壁面处速度梯度较大。 8. 升力如果流体为空气,通常升力被称为气动力(aerodynamic force) 升力可以和曳力一起讨论,两者表达式相同,曳力平行于流动方向,升力垂直于流动方向。若升力系数为\(C_L\),则 \[F=\frac{1}{2}\rho_g u_s^2 A_p C_L \]三、终端速度颗粒在静止流体中自由沉降,达到受力平衡时的速度为终端速度。此时颗粒浮力、重力、曳力三者平衡。 \[\rho_p V_p g - \rho_g V_p g - \frac{1}{2}\rho_g u_s^2 A_p C_D = 0 \]\[u_T=\sqrt{\frac{4d(\rho_p-\rho_g)g}{3\rho_g C_D}} \]由此\(C_D\)是\(Re\)的函数,而\(Re\)与颗粒速度相关,因此上式需要迭代求解。 |
【本文地址】
今日新闻 |
推荐新闻 |