基于Householder变换完成QR分解进而求解实(复)矩阵的逆矩阵

您所在的位置：网站首页 › 矩阵逆的几何意义 › 基于Householder变换完成QR分解进而求解实(复)矩阵的逆矩阵

基于Householder变换完成QR分解进而求解实(复)矩阵的逆矩阵

2024-07-12 10:27| 来源: 网络整理| 查看: 265

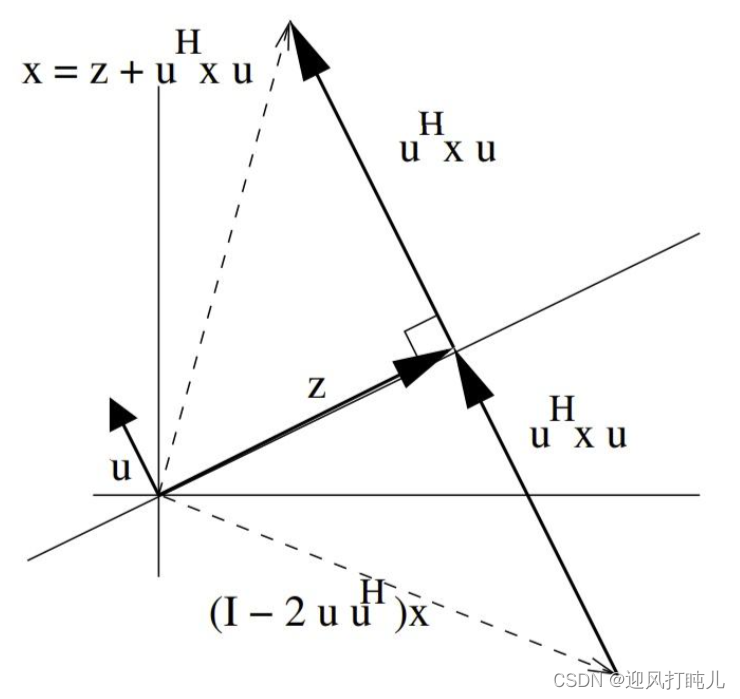
基于Householder变换完成QR分解进而求解逆矩阵，实矩阵和复矩阵都适用

前言

一、Householder变换简介

二、Householder矩阵

三、Householder矩阵的性质

四、Householder变换及几何意义

五、Householder变换进行QR分解

六、例1 Householder变换

七、例2 实矩阵QR分解

八、例3 复矩阵QR分解

九、求逆矩阵

十、计算量分析

十一、MATLAB仿真

1、实矩阵仿真

2、复矩阵仿真

十二、参考资料

总结

前言

今天花时间认真研究了Householder变换，理解了它变换的几何意义，以及怎样用它将可逆矩阵分解成Q矩阵和R矩阵。本文将站在我个人理解的基础上阐述什么是Householder变换及它的几何意义，同时也会通过列举几个例子说明如何将一个矩阵通过Householder变换分解为Q矩阵和R矩阵，例子中待分解的矩阵包括实矩阵和复矩阵。另外，也会分析该算法的计算复杂度，找出各种运算次数和矩阵阶次之间的关系。最后，会用MATLAB进行仿真，当然，代码也会分享出来。

提示：以下是本篇文章正文内容，希望能帮助到各位，转载请附上链接。

一、Householder变换简介

householder变换（Householder transformation），译为“豪斯霍尔德变换”，或译“豪斯霍德转换”，又称初等反射（Elementary reflection），最初由A.C Aitken在1932年提出。householder变换最初由A.C Aitken在1932年提出。Alston Scott Householder在1958年指出了这一变换在数值线性代数上的意义。这一变换将一个向量变换为由一个超平面反射的镜像，是一种线性变换。其变换矩阵被称作豪斯霍尔德矩阵，在一般内积空间中的类比被称作豪斯霍尔德算子。超平面的法向量被称作豪斯霍尔德向量。

Householder变换是一种重要的矩阵变换方法，用于将一个向量通过相似变换转化为另一个向量。它可以被用来实现许多数值计算任务，如矩阵的QR分解、线性方程组求解、特征值计算等。

Householder变换可以将向量的某些元素置零，同时保持该向量的范数不变。

二、Householder矩阵

Householder矩阵定义为：

$\mathbf{H}=\mathbf{I}-\frac{2}{\langle\mathbf{v},\mathbf{v}\rangle}\mathbf{v}\mathbf{v}^{H}$

即

$\textbf{H}=\textbf{I}-\frac{2\textbf{vv}^H}{\textbf{v}^H\textbf{v}}$

其中 I 为单位矩阵，其中householder向量v满足：

$\mathbf{v}=\mathbf{x}+\mathrm{sgn}(x_1)\|\mathbf{x}\|_2\mathbf{e}_1$

其中 $\mathrm{sgn}(x_1)$ 表示向量 $\textbf{x}$ 的第一个元素的归一化处理，即

$\mathrm{sgn}(x_1)=\frac{x_1}{\left |x_1 \right |}$

看其他文章，对于实数，全将 $\mathrm{sgn}(\mathbf{x}_1)$ 当成 -1处理，确实也没问题。实际上，实数在这里变成了符号函数，但是0的符号必须为1或-1，不能为0，不然算不出来，编程验证过，为求简单，实数直接用-1好了。

一般，我们会对v进行归一化处理，那么归一化后 Householder矩阵可写为：

$\textbf{H}=\textbf{I}-2 \textbf{vv}^H$

三、Householder矩阵的性质

① Householder变换矩阵是共轭对称矩阵，因为

$\textbf{H}^H=(\textbf{I}-2\textbf{vv}^H)^{H}=\textbf{H}$

② Householder变换矩阵是正交矩阵，因为

$\textbf{HH}^H=(\textbf{I}-2\textbf{vv}^H)*(\textbf{I}-2\textbf{vv}^H)=\textbf{I}$

③ Householder变换矩阵是对合的，因为

$\textbf{H}^2=\textbf{HH}=(\textbf{I}-2\textbf{vv}^H)*(\textbf{I}-2\textbf{vv}^H)=\textbf{I}$

四、Householder变换及几何意义

对于任意与向量 v 垂直的向量 z（即 $\textbf{v}^{H}\textbf{z}=0$ ）,经Householder变换矩阵旋转，其值不变

$\textbf{Hz}=\textbf{z}-2\textbf{v}(\textbf{v}^H\textbf{z})=\textbf{z}$

任意向量 x 都可以写成如下形式

$\textbf{x}=\textbf{z}+\textbf{v}^H\textbf{xv}$

其中 z 是 x 中与向量 v 垂直的成分， $\textbf{v}^H\textbf{xv}$ 是 x 中与向量 v 同向的成分，则经过Householder变换矩阵旋转后：

$\textbf{y}=\textbf{Hx}=\textbf{Hz}+\textbf{H}\textbf{v}^H\textbf{xv}=\textbf{z}+(\textbf{I}-2\textbf{vv}^H)\textbf{v}^H\textbf{xv}=\textbf{z}-\textbf{v}^H\textbf{xv}$

对照旋转前向量 x 可见：与向量 v 垂直的分量保持不变，与其同向分量方向相反。二维形式如下（这里u=v）旋转后向量 y 与旋转前向量 x 关于与向量 v 垂直的法平面呈镜像，因此Householder变换也称为Householder 反射。另外还需要注意，旋转前后向量模长不变。

五、Householder变换进行QR分解

由householder变换的性质，可以使n维非零向量

$\mathrm{\textbf{a}1=[a_{11},a_{21},\cdots,a_{n1}]^T}$

变换为

$[\times,0,0\text{,}\cdots,0]^\mathrm{T}$

因此可以对矩阵A按列进行分块，即

$\mathrm{\textbf{A}=[\textbf{a}_1,\textbf{a}_2,\cdots,\textbf{a}_n]}$

$\mathrm{\textbf{a}_i=[a_{1i},a_{2i},\cdots,a_{ni}]^T}$

首先对a1进行变换，令x=a1，则

$\mathbf{v}=\mathbf{x}+\mathrm{sgn}(\mathbf{x}_1)\|\mathbf{x}\|_2\mathbf{e}_1$

$\textbf{H}_1=\textbf{I}-2 \textbf{vv}^H$

变换为

$[\times,0,0\text{,}\cdots,0]^\mathrm{T}$

那么就可以得到

$\left.\mathrm{\textbf{H}_1\textbf{A}=\textbf{H}_1[\textbf{a}_1,\textbf{a}_2,\cdots,\textbf{a}_n]=\left|\begin{array}{cccc}\times&\mathrm{a}_{12}^*&\cdots&\mathrm{a}_{1n}^*\\0&\mathrm{a}_{22}^*&\cdots&\mathrm{a}_{2n}^*\\\vdots&\vdots&\ddots&\vdots\\0&\mathrm{a}_{\mathrm{n2}}^*&\cdots&\mathrm{a}_{\mathrm{nn}}^*\end{array}\right. |}\right|$

重复上次方法对

$\begin{array}{|ccc|}\mathrm{a_{22}^{**}}&\cdots&\mathrm{a_{2n}^{**}}\\\vdots&\ddots&\vdots\\\mathrm{a_{n2}^{**}}&\cdots&\mathrm{a_{nn}^{*}}\end{array}$

的第一列进行变换，同理计算得到householder矩阵为 $\textbf{H}_{2}^{*}$

$\begin{bmatrix}1 &0 \\ 0 & \textbf{H}_{2}^{*}\end{bmatrix} \mathrm{\textbf{H}_1\textbf{A}=\textbf{H}_2\textbf{H}_1[\textbf{a}_1,\textbf{a}_2,\cdots,\textbf{a}_n]}=\begin{vmatrix}\times&\times&\mathrm{a_{13}^{**}}&\cdots&\mathrm{a_{1n}^{**}}\\0&\times&\mathrm{a_{23}^{**}}&\cdots&\mathrm{a_{2n}^{**}}\\0&0&\mathrm{a_{33}^{**}}&\cdots&\mathrm{a_{3n}^{**}}\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&\mathrm{a_{n3}^{**}}&\cdots&\mathrm{a_{nn}^{**}}\end{vmatrix}$

重复上面的步骤，做n-1次变换后，就可以得到一个上三角矩阵R

$\mathrm{\textbf{H}_{n-1}\textbf{H}_{n-2}\cdots \textbf{H}_1\textbf{A}}=\begin{vmatrix}\times&\times&\times&\cdots&\times\\0&\times&\times&\cdots&\times\\0&0&\times&\cdots&\times\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&\times\end{vmatrix}$

由于H是正交矩阵，因此多个正交矩阵相乘依然是正交矩阵，并且正交矩阵的逆等于矩阵的转置，所以可以得到

$\textbf{Q}=\textbf{H}_1\textbf{H}_2\cdots \textbf{H}_n$

$\textbf{A}=\textbf{QR}$

至此，便成功利用Householder进行了QR分解。

六、例1 Householder变换

设 $\textbf{x}=(1,2,2)^{\intercal}$ ，用Householder变换化x为与 $\textbf{e}_1=[1\; 0 \; 0]$ 同方向的向量。

计算

$|x|=3,x-|x|e_{1}=2(-1,1,1)^{T}.$

取

$v=\frac{1}{\sqrt{3}}(-1,1,1)^{\intercal}$

则

$\begin{aligned}\textbf{H}&=\begin{bmatrix}1\\&1\\&&1\end{bmatrix}-\frac{2}{3}\begin{bmatrix}-1\\1\\1\end{bmatrix}[-1,1,1]=\frac{1}{3}\begin{bmatrix}1&&2&&2\\2&&1&&-2\\2&&-2&&1\end{bmatrix}\end{aligned}$

则

$\textbf{Hx}=3\boldsymbol{\textbf{e}}_1$

七、例2 实矩阵QR分解

已知矩阵 $\left.A=\left[\begin{matrix}0&4&2\\0&3&1\\2&1&-2\end{matrix}\right.\right]$ ，用Householder进行QR分解。

记

$\mathrm{\textbf{A}=[\textbf{a}_1,\textbf{a}_2,\textbf{a}_3]}$

记

$\alpha_{1}=\left\|\textbf{a}_{1}\right\|_{2}=2$

令

$\textbf{v}_{1}=\frac{\textbf{a}_{1}-\alpha_{1}\textbf{e}_{1}}{\left\|\textbf{a}_{1}-\alpha_{1}\textbf{e}_{1}\right\|_{2}}=\frac{1}{\sqrt{2}}(-1,0,1)^{T}$

则

$\left.\textbf{H}_1=\textbf{I}-2\textbf{v}_1\textbf{v}_1^H=\left(\begin{matrix}0&0&1\\0&1&0\\1&0&0\end{matrix}\right.\right)$

从而

$\left.\textbf{H}_1\textbf{A}=\left(\begin{array}{ccc}2&1&2\\0&4&-2\\0&3&1\end{array}\right.\right)$

记

$\boldsymbol\beta=\left(3,4\right)^{T}$

记

$\alpha_{2}=\left\|\boldsymbol\beta\right\|_{2}=5$

令

$\textbf{v}_{2}=\frac{\boldsymbol\beta-\alpha_{2}\textbf{e}_{2}}{\left\|\boldsymbol\beta-\alpha_{2}\textbf{e}_{2}\right\|_{2}}=\frac{1}{\sqrt{5}}(-1,2)^{T}$

则

$\left.\tilde{\textbf{H}}_2=\textbf{I}-2\textbf{v}_2\textbf{v}_2^H=\frac{1}{5}\left(\begin{matrix}3&4\\4&-3\end{matrix}\right.\right)$

记

$\textbf{H}_2=\begin{bmatrix} 1 & \\ & \tilde{\textbf{H}}_2\end{bmatrix}=\begin{bmatrix} 1 &0 &0 \\ 0& \frac{3}{5}& \frac{4}{5} \\ 0 & \frac{4}{5} & \frac{-3}{5} \end{bmatrix}$

则

$\left.\textbf{H}_2(\textbf{H}_1\textbf{A})=\left(\begin{array}{ccc}2&1&-2\\0&5&\frac{11}{5}\\0&0&\frac{-2}{5}\end{array}\right.\right)=\textbf{R}$

所以

$\textbf{Q}=\textbf{H}_1\textbf{H}_2=\begin{bmatrix}0&0&1\\0&1&0\\1&0&0\end{bmatrix}\begin{bmatrix} 1 &0 &0 \\ 0& \frac{3}{5}& \frac{4}{5} \\ 0 & \frac{4}{5} & \frac{-3}{5} \end{bmatrix}=\begin{bmatrix} 0 & \frac{4}{5} & \frac{-3}{5} \\ 0& \frac{3}{5}& \frac{4}{5} \\ 1 &0&0 \end{bmatrix}$

故

$\textbf{A}=\textbf{QR}=\begin{bmatrix} 0 & \frac{4}{5} & \frac{-3}{5} \\ 0& \frac{3}{5}& \frac{4}{5} \\ 1 &0&0 \end{bmatrix} \begin{bmatrix}2&1&-2\\0&5&\frac{11}{5}\\0&0&\frac{-2}{5}\end{bmatrix}=\begin{bmatrix}0&4&2\\0&3&1\\2&1&-2\end{bmatrix}$

八、例3 复矩阵QR分解

复矩阵就不写具体题目了，需要注意的是，计算householder向量v时用以下公式

$\mathbf{v}=\mathbf{x}+\mathrm{sgn}(x_1)\|\mathbf{x}\|_2\mathbf{e}_1$

其中 $\mathrm{sgn}(x_1)$ 表示向量 $\textbf{x}$ 的第一个元素的归一化处理，即

$\mathrm{sgn}(x_1)=\frac{x_1}{\left |x_1 \right |}$

九、求逆矩阵

分解得到Q矩阵和R矩阵后可参考下面两篇文章进行求逆矩阵：

施密特正交化QR分解求逆矩阵与MATLAB仿真_qr分解法求逆矩阵-CSDN博客

一种基于约化因子上三角矩阵求逆方法与MATLAB仿真-CSDN博客

https://download.csdn.net/download/m0_66360845/89039765https://download.csdn.net/download/m0_66360845/89039765

十、计算量分析

省略，算起来比较复杂，涉及乘法、加法、除法、开方。

等什么时候很闲，再来分析一下咯。

十一、MATLAB仿真 1、实矩阵仿真

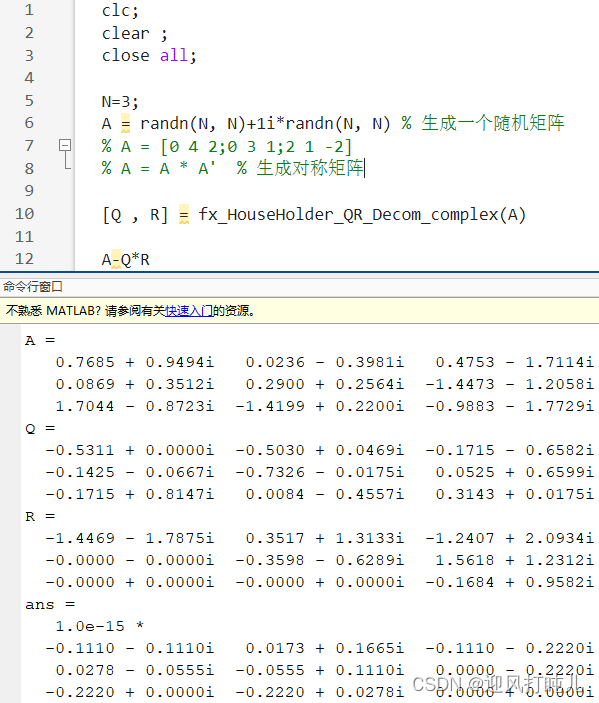
可见，与上面算的例题结果吻合。

2、复矩阵仿真

十二、参考资料

参考资料：https://download.csdn.net/download/m0_66360845/89039765https://download.csdn.net/download/m0_66360845/89039765

总结

以上就是今天要讲的内容，本文介绍了Householder变换，在我理解的基础上讲解了它变换的几何意义，以及怎样用它将可逆矩阵分解成Q矩阵和R矩阵。同时，也用MATLAB验证了Householder变换 QR分解算法。

【本文地址】

基于Householder变换完成QR分解进而求解实(复)矩阵的逆矩阵

基于Householder变换完成QR分解进而求解实(复)矩阵的逆矩阵

今日新闻

推荐新闻