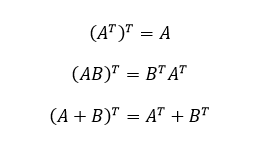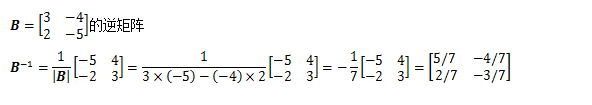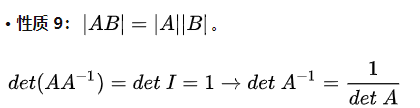a = [ a b c d ] (1) a= \left[ \begin{matrix} a & b \\ c & d \\ \end{matrix} \right] \tag{1} a=[ac​bd​](1) b = [ a 1 a 2 b 1 b 2 ] (2) b= \left[ \begin{matrix} a1 & a2 \\ b1& b2 \\ \end{matrix} \right] \tag{2} b=[a1b1​a2b2​](2)

两个矩阵相加或相减，需要满足两个矩阵的列数和行数一致。

加法交换律：A + B = B + A a + b = [ a + a 1 b + a 2 c + b 1 d + b 2 ] (1) a+b= \left[ \begin{matrix} a+a1 & b+a2 \\ c+b1& d+b2 \\ \end{matrix} \right] \tag{1} a+b=[a+a1c+b1​b+a2d+b2​](1)

a − b = [ a − a 1 b − a 2 c − b 1 d − b 2 ] (1) a-b= \left[ \begin{matrix} a-a1 & b-a2 \\ c-b1& d-b2 \\ \end{matrix} \right] \tag{1} a−b=[a−a1c−b1​b−a2d−b2​](1)

两个矩阵A和B相乘，需要满足A的列数等于B的行数。 a矩阵的行元素乘以每一列然后相加作为新矩阵的行元素 a ∗ b = [ a ∗ a 1 + b ∗ b 1 a ∗ a 2 + b ∗ b 2 c ∗ a 1 + d ∗ b 1 c ∗ a 2 + d ∗ b 2 ] (1) a*b= \left[ \begin{matrix} a*a1+b*b1 & a*a2+b*b2 \\ c*a1+d*b1& c*a2+d*b2 \\ \end{matrix} \right] \tag{1} a∗b=[a∗a1+b∗b1c∗a1+d∗b1​a∗a2+b∗b2c∗a2+d∗b2​](1)

矩阵乘法不满足交换律，但是满足分配率和结合律,也就是说AB不等于BA (AB)C=A(BC) (A+B)C=AC+BC C(A+B)=CA+CB

g*(AB)=(gA)B=A(gB) g属于实数

a矩阵转置之后(行变成列，列变成行)

a T = [ a c b d ] (1) aT= \left[ \begin{matrix} a & c \\ b & d \\ \end{matrix} \right] \tag{1} aT=[ab​cd​](1) 转置性质：：

矩阵A的逆矩阵记作A’， A A’=A’A= I，I是单位矩阵。 先介绍一下矩阵的单位阵，就是单位矩阵是一个n×n矩阵，从左到右的对角线上的元素是1，其余元素都为0。

c = [ 1 0 0 1 ] (1) c= \left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \tag{1} c=[10​01​](1)

d = [ 1 0 0 0 1 0 0 0 1 ] (2) d= \left[ \begin{matrix} 1 & 0 &0 \\ 0 & 1 &0\\ 0 & 0 &1 \\ \end{matrix} \right] \tag{2} d=⎣⎡​100​010​001​⎦⎤​(2) 性质：ac=ca=a

如果一个矩阵转置后等于原矩阵，那么这个矩阵称为对称矩阵。由定义可知，对称矩阵一定是方阵。一个矩阵转置和这个矩阵的乘积就是一个对称矩阵：

性质1：单位矩阵的行列式为 1 ，与之对应的是单位立方体的体积是 1。 性质 2：当两行进行交换的时候行列式改变符号。 性质 3：行列式是单独每一行的线性函数（其它行不变）。 性质4：矩阵中有俩行一样，矩阵的行列式为0。 性质 5：用矩阵的一行减去另一行的倍数，行列式不变。 性质 6：当矩阵的某一行全为零的时候，行列式为零。 性质 7：如果矩阵是三角形的，那么行列式等于对角线上元素的乘积。 d = [ 1 0 0 0 1 0 0 0 1 ] (2) d= \left[ \begin{matrix} 1 & 0 &0 \\ 0 & 1 &0\\ 0 & 0 &1 \\ \end{matrix} \right] \tag{2} d=⎣⎡​100​010​001​⎦⎤​(2)

性质 8：如果矩阵是可逆的那么矩阵的行列式不等于0，反之行列式为0

性质 10：转置矩阵的行列式不变