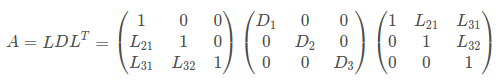解方程AX=b与矩阵分解:奇异值分解(SVD分解) 特征值分解 QR分解 三角分解 LLT分解 |
您所在的位置:网站首页 › 矩阵如何求解方程组 › 解方程AX=b与矩阵分解:奇异值分解(SVD分解) 特征值分解 QR分解 三角分解 LLT分解 |
解方程AX=b与矩阵分解:奇异值分解(SVD分解) 特征值分解 QR分解 三角分解 LLT分解
|
目录 1. 前言 1.1 为什么要进行矩阵分解? 1.2 矩阵与矩阵分解的几何意义? 2. LU三角分解 3. Cholesky分解 — LDLT分解 4. Cholesky分解 — LLT分解 5. QR分解 6. 奇异值分解 7. 特征值分解 本文转自大佬博客:https://blog.csdn.net/Hansry/article/details/104174651 1. 前言本博客主要介绍在SLAM问题中常常出现的一些线性代数相关的知识,很早就想整理一下了,刚好看到Manii 的博客对矩阵分解的方法进行了总结,以方便求解线性方程组AX=B。在基于《计算机视觉—算法与应用》附录A 的内容 ,重点介绍了各种分解的适用情况、分解的特点。 1.1 为什么要进行矩阵分解?1、矩阵分解可以在一定程度上降低存储空间,可以大大减少问题处理的计算量(如对一个矩阵进行求逆、求解方程组等),从而高效地解决目标问题。 2、矩阵分解可以提高算法的数值稳定性。 1.2 矩阵与矩阵分解的几何意义?在矩阵分解中,我们常常期望将矩阵分解成正交矩阵、对角矩阵以及上三角(下三角)矩阵的乘积。以三维矩阵为例,一个普通矩阵的几何意义是对坐标进行某种线性变换,而正交矩阵的几何意义是坐标的旋转,对角矩阵的几何意义是坐标的缩放,三角矩阵的几何意义是对坐标的切边。因此对矩阵分解的几何意义就是将这种变换分解成缩放、切边和旋转的过程。 2. LU三角分解三角分解又称为LU分解或LR分解,是将原正方(square)矩阵分解成一个上三角矩阵和一个下三角矩阵。
其中L是单位下三角矩阵,D是对角矩阵,U是单位上三角矩阵。 3. Cholesky分解 — LDLT分解假设矩阵A为对称矩阵,且任意K阶主子式均不为0时(即正定),A有如下唯一的分解形式:
即L为下三角单位矩阵,D为对角矩阵。LDLT方法实际上是Cholesky分解法的改进(LLT分解需要开平方),具体代码可见Chelesky分解LDLT用于求解线性方程组。 注:一个对称矩阵A是正定的充要条件是对任何非零向量 x 有 这里举个例子,比如VINS的初始化过程中,在做视觉sfm和IMU预积分的PVQ对齐的时候(即在initial_alignment.cpp文件中的LinearAlignment()函数中),会在对齐流程的第3步利用平移约束估计重力、速度和尺度初始值时用到ldlt来求解待优化的变量[v0, v1, ...vn, g, s]。构建H△x=b的形式进行优化参数求解,具体代码如下: /** * @brief 求解各帧的速度,枢纽帧的重力方向,以及尺度 * * @param[in] all_image_frame * @param[in] g * @param[in] x * @return true * @return false */ bool LinearAlignment(map &all_image_frame, Vector3d &g, VectorXd &x) { // 这一部分内容对照论文进行理解 // 这里是《VIO 第7讲》 —— 视觉与IMU对齐估计流程第3步:利用平移约束估计重力、速度以及尺度初始值 int all_frame_count = all_image_frame.size(); int n_state = all_frame_count * 3 + 3 + 1; // 速度 + 重力 + 尺度因子 MatrixXd A{n_state, n_state}; A.setZero(); VectorXd b{n_state}; b.setZero(); map::iterator frame_i; map::iterator frame_j; int i = 0; for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i ++, i ++) { frame_j = next(frame_i); MatrixXd tmp_A(6, 10); tmp_A.setZero(); VectorXd tmp_b(6); tmp_b.setZero(); double dt = frame_j->second.pre_integration->sum_dt; // 《VIO第7讲》,公式(17) tmp_A.block(0, 0) = -dt * Matrix3d::Identity(); tmp_A.block(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity(); tmp_A.block(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0; tmp_b.block(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0]; // cout delta_p.transpose() second.R.transpose() * frame_j->second.R; tmp_A.block(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity(); tmp_b.block(3, 0) = frame_j->second.pre_integration->delta_v; // cout delta_v.transpose() |
【本文地址】
今日新闻 |
推荐新闻 |