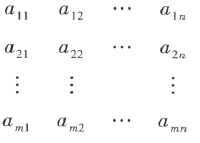机器学习之数学基础(二)～数组、向量、矩阵、向量空间、二维矩阵

您所在的位置：网站首页 › 矩阵向量空间的维数 › 机器学习之数学基础(二)～数组、向量、矩阵、向量空间、二维矩阵

机器学习之数学基础(二)～数组、向量、矩阵、向量空间、二维矩阵

2024-07-15 13:39| 来源: 网络整理| 查看: 265

1. 概述

在学习机器学习(machine learning)或模式识别(pattern recognition)过程中，我经常会困惑于向量、数组和矩阵这三种数据结构，而在学习张学工教授《模式识别》一书时，我又碰到了二维矩阵这个对我很模糊的概念，一生气就自己总结一个吧。

本文如有不足不对之处，欢迎指正。

2. 数组、向量、矩阵和向量空间 2.1 数组

[转载自：https://blog.csdn.net/qq_41800366/article/details/86605575]

概念：所谓数组，是有序的元素序列。这里的概念就没有涉及到空间了，我们通常称的n维数组，这里的维度指的不是空间的维度，而是数据所构成的维度；下面进行举例说明，

一维数组 [1, 2, 3, 4] 这里的数据的维度就只有一维，也就是深度为1，怎么理解呢，比如你要取2，你要怎么做呢，只需要进入第一层，这时候你会找到1，2，3，4这四个元素，直接就能找到2这个元素。二维数组 [[1, 2],[3, 4]] 这里的数据的维度就就有二维，也就是深度为2，怎么理解呢，比如你要取2，你要怎么做呢，首先你要进入进入第一层，这时候你找到的是[1, 2] 和 [3, 4]，然后你还得继续往下找，再进入一层，你会找到 1，2，3，4这四个元素，然后找到2这个元素，也就是你进入了两层才找到元素，所以深度为2，维度为二维。三维数组[[[1, 2], [3, 4]], [[5, 6], [7, 8]]]

Note: 我个人认为数组最大的用处是在python等编程语言中实现向量、矩阵等数据结构！这里的数据的维度就就有三维，也就是深度为3，怎么理解呢，比如你要取2，你要怎么做呢，首先你要进入进入第一层，这时候你找到的是[[1, 2], [3, 4]] 、 [[5, 6], [7, 8]] ，然后你还得继续往下找，再进入一层，你会找到 [1, 2]、[3, 4]、[5, 6]、 [7, 8] ，然后你还得继续往下找，再进入一层，1、2、3、4、5、6、7、8这8个元素，然后找到2这个元素，也就是你进入了三层才找到元素，所以深度为3，维度为三维。

2.2 n维向量

概念：n个有次序的数 $a_{1}$ , $a_{2}$ , ····, $a_{n}$ 所组成的数组称为n维向量，这n个数称为该向量的n个分量，第i个数 $a_{i}$ 称为第i个分量。(同济大学线性代数第五版-4.1)

n维向量可写成一行，也可写成一列，分别称为行向量和列向量，也就是行矩阵和列矩阵，并规定行向量和列向量都按矩阵的运算规则进行运算。因此，n维列向量

与n维行向量

$a^{T}=(a_{1},a_{2},\cdot \cdot \cdot ,a_{n})$

Note: 这个解释其实是说在线性代数中，向量和矩阵其实是一回事。不同的是矩阵论阶，向量论维。

在解析几何中，我们把“既有大小又有方向的量”叫做向量，并把可随意平行移动的有向线段作为向量的几何形象。

在引进坐标系以后，这种向量就有了坐标表示式— — 三个有次序的实数，也就是本书中的3维向量。因此，当　n ≤ 3 时，n维向量可以把有向线段作为几何形象，但当n＞3 时，n 维向量就不再有这种几何形象，只是沿用一些几何术语罢了。

2.3 矩阵

在同济大学线性代数第六版中，矩阵定义如下：由m×n 个数aij （i= 1，2，…，m；j= 1，2，…，n）排成的m 行n 列的数表

称为m 行n 列矩阵，简称m×n 矩。

矩阵的列向量组和行向量组都是只含有限个向量的向量组；反之，一个含有限个向量的向量组总可以构成一个矩阵。因此可知向量可以组成矩阵，矩阵是包含向量的。

2.4 向量空间

几何中，“空间”通常是作为点的集合，即构成“空间”的元素是点，这样的空间叫做点空间。

我们把3 维向量的全体所组成的集合叫做3 维向量空间。

$\mathbb{R}^{T}=\left \{ r= (x,y,z)^{T}|x,y,z\in \mathbb{R} \right \}$

在点空间取定坐标系以后，空间中的点P（x，y，z）与3 维向量　r =（x，y，z）T 之间有一一对应的关系。

类似的，n维向量的全体所组成的集合叫做n维向量空间。

$\mathbb{R}^{n}=\left \{ x= (x_{1},x_{2},\cdot \cdot \cdot ,x_{n})^{T}|x_{1},x_{2},\cdot \cdot \cdot ,x_{n}\in \mathbb{R} \right \}$

Note: 这里n维向量空间的概念应该可以理解成n x n矩阵。

在同济大学线性代数第六版中，矩阵的列向量组和行向量组都是只含有限个向量的向量组；反之，一个含有限个向量的向量组总可以构成一个矩阵。例如，一个mxn矩阵的全体列向量是一个含n个m维列向量的向量组。

向量空间(同济大学线性代数第五版)

概念：设V为n维向量的集合，如何集合V非空，且集合V对于向量的加法及乘法两种运算封闭，那么就称集合V为向量空间。

封闭，是指在集合V中可以进行向量的加法及乘法两种运算。具体地说， $if a \in V, b\in V, then a+b\in V; if a\in V, \lambda \in V, then \lambda a\in V$ $若a\in V, b\in V, 则a+b\in V；若a\in V, \lambda \in \mathbb{R}, 则\lambda a\in V.$