坐标系变换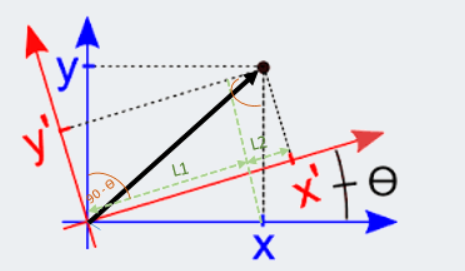

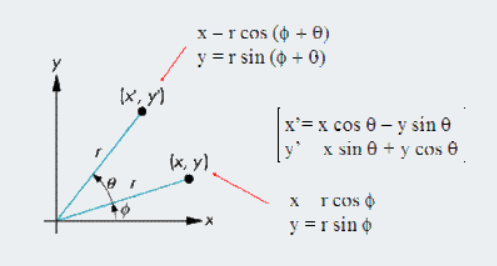
$$对坐标系旋转\theta 可以得到新的坐标系，则向量A在两个坐标系下的坐标分别为： $$$$ A=A^x e_x+A^y e_y $$$$ A=A^′x e_x+a^′y e_y $$$$ 其中A^{′x}=L_1+L_2 $$$$ L_1=A^x cos⁡(\theta ) $$$$ L_2=A^y cos⁡(\pi/2−\theta ) $$$$ 则(A^′)^x= A^x cos⁡(\theta )+A^y cos⁡(\pi/2−\theta ) $$$$ 同理 A^′y= A^x cos⁡(\pi/2+\theta )+A^y cos⁡(\theta ) $$$$ 则A'就可以表示成矩阵的乘法: $$$$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & sin(\theta) \\\\ -sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$

基向量变换

$$在新的基向量上表示旋转后的向量，对于向量逆时针旋转\theta 相当于顺时针将坐标系旋转\theta $$ $$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & -sin(\theta) \\\\ sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$$$ dx^{′1}=(\partial x^{′1})/(\partial x^{1} ) dx^1+(\partial x^{′1})/(\partial x^2 ) dx^2 $$$$ dx^{′2}=(\partial x^{′2})/(\partial x^1 ) dx^1+(\partial x^{′2})/(\partial x^2 ) dx^2 $$$$ dx^{'i}=\frac{\partial x^{'i}}{\partial x^j} dx^j $$$$ 计算适当的导数我们得到: $$$$ \frac{\partial x^{'1}}{\partial x^1} = cos\theta \qquad \frac{\partial x^{'2}}{\partial x^1} = sin \theta $$$$ \frac{\partial x^{'1}}{\partial x^2} = -rsin\theta \qquad \frac{\partial x^{'2}}{\partial x^2} = rcos\theta $$$$ 因为dx^{'1}和d^{'2}实际上反映了e_1 和e_2 的大小所以: $$$$ e_1 = \frac{\partial x^{'1}}{\partial x^1} \vec{i} +\frac{\partial x^{'2}}{\partial x^1} \vec{j} = cos \theta \vec{i}+\ sin\theta vec{j} e_2 = \frac{\partial x^{'1}}{\partial x^2} \vec{i} +\frac{\partial x^{'2}}{\partial x^2} \vec{j} = -rsin\theta \vec{i} + rcos\theta \vec{j} $$$$这样我们就得到了分量A^{'i}的定义,又称为逆变(反变或contravariant)分量 $$$$ A^{'i} = \frac{\partial x^{'i}}{\partial x^j} A^j $$

协变分量和逆变分量

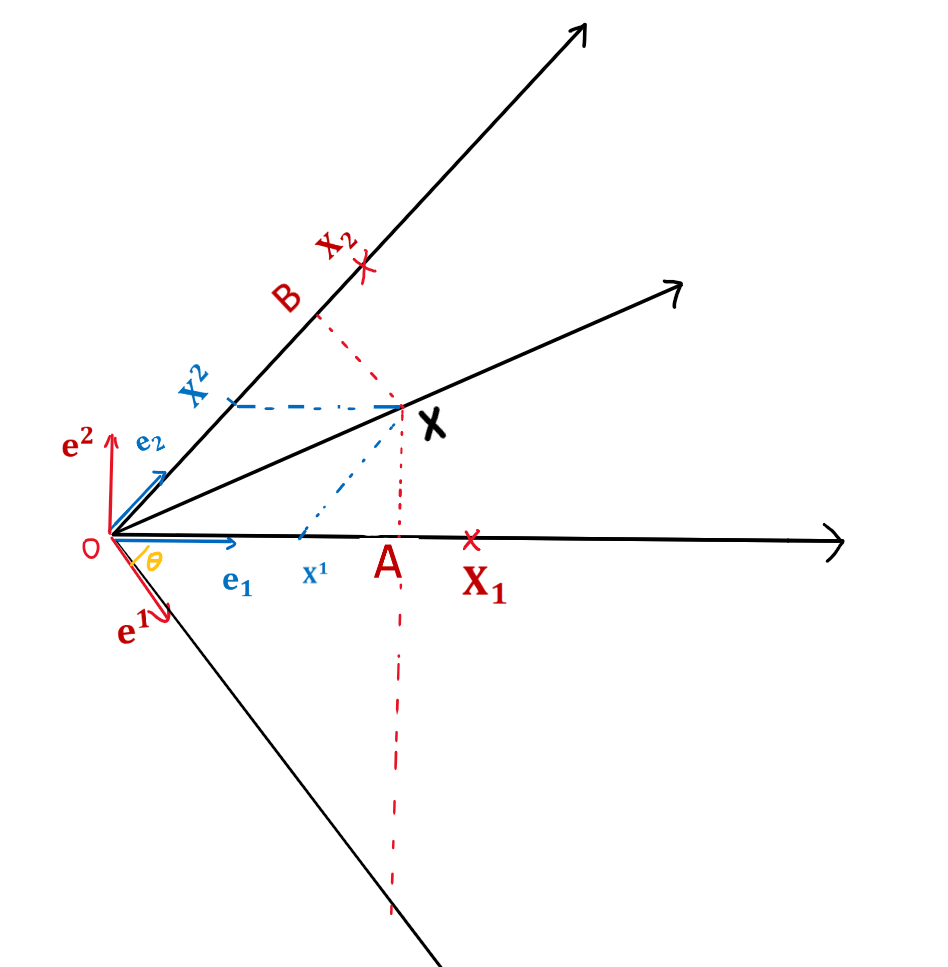
$$ 图中 X = e_1 x^1+e_2 x^2 $$$$ 我们构造了e_1 和 e_2 的对偶向量e^1 和 e^2，我们希望用对偶向量表示原向量X $$$$ 我们令 协变分量为 x_1= e_1 x ，注意协变分量是标量 $$$$ 我们期望的结果是: X = e^1 X_1+e^2 X_2 $$$$ 对偶向量是对于e^i满足\lt e^i,e_j \gt =\delta_j^i 的向量e^j $$$$ 举个例子:e^1 是 e_1 的对偶向量，他满足 e^1 \cdot e_1=1 $$$$ 即对偶空间的相同下标的基向量内积为1， 关于对偶空间和对偶基可以看： $$ https://blog.csdn.net/sumx2015/article/details/78909635 解释的很形象了 $$ 对偶基的要求还蕴含了任意非相同标记的基向量和对偶基向量内积为0，就是说他们垂直 $$$$ 下面我们来证明为什么这样的向量可以构造出来新的基底 $$$$ 由图根据平行四边形法则我们可知: $$$$ |x|sin\theta =|e^1 x_1 |cos\theta $$$$ sin\theta =\frac{|e^1 (e_1 x)|}{|x|} cos\theta $$$$ sin\theta =\frac{|e^1 | e_1 |cos⁡(\pi/2−\theta ) |}{|x|} cos\theta $$$$ 1 = |e^1| |e_1|cos\theta $$$$ 即e^1 e_1=1 , 同理可以证明e^2 e_2=1 $$$$ 反过来 也可以推导出 |x|sin\theta =|e^1 x_1 |cos\theta $$$$ 所以\lt e^i,e_j\gt =\delta_{j}^{i} 是满足协变分量为x_1= \lt e_1 ,x\gt 的原向量X在对偶空间上的表示 $$$$ 尤其是当 e_1=1时，A点就和 X_1 重合了，此时X_1 就是x在 e_1 轴上的投影 $$$$ 对于逆变分量， 如果改变基向量e_1 的大小，为了保证X= e则逆变分量X^1 的大小会反向改变, $$ 比如基向量减小 一半，逆变分量就会增加一倍， 而对于协变分量，如果原空间的基向量模增加一倍， 对偶空间的基向量模减小一倍，因为内积为1的约束， 对应协变分量就增加一倍，所以 协变指的是，随着原空间的基向量的变化而正相关变化 之前我们推导对于逆变张量的分量: $$ A^{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A^j $$$$ 同理对协变张量的分量效果也是一致的： $$$$ A_{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A_j $$

张量的缩放

当把上面的逆变张量和协变张量推广到普通情况就相当复杂: $$ 令原张量表示成: S_{j_1 j_2⋯j_q}^{i_1 i_2⋯i_p } $$$$ 则经过变换后的矩阵\bar{S}可以表示成： $$$$ \bar{S}_{j_1 j_2⋯j_q}^{i_1 i_2⋯i_p}= S_{\beta_1 \beta_2⋯\beta_q}^{\alpha_1 \alpha_2⋯\alpha_p}\frac{\partial \bar{x}^{i_1 }}{\partial x^{\alpha_1}} \frac{\partial \bar{x}^{i_2 }}{\partial x^{\alpha_2}}\cdots \frac{\partial \bar{x} ^{i_p }}{\partial x^{\alpha_p } } \frac{\partial \bar{x} ^ {\beta_1}}{\partial x^{j_1}} \frac{\partial \bar{x} ^{\beta_2}}{\partial x^{j_2 }}\cdots \frac{\partial \bar{x} ^{\beta_p }}{\partial x^{j_q }} $$$$ 当我们尝试让某个上标i_k 和某个下标j_b 相等时，就可以在右式中约去， $$$$ 反映到左式中就可以直接约去，我们把这种操作叫做contraction $$$$ 张量压缩，当然我们也可以进行扩张，制造两个相同的下标。 $$$$ 度量张量最有用的功能之一就是在其他张量的协变量和范变量分量之间进行转换 $$$$ 因为对 度规张量进行变换可以得到： $$$$ g_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^\nu} \frac{\partial \xi ^\beta}{\partial x^\nu} $$$$ g^{'}_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^{'\nu}} \frac{\partial \xi ^\beta}{\partial x^{'\nu}} = \eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma}\frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} =\eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} = g_{\sigma \rho}\frac{\partial x^\sigma}{\partial x^{'\mu} }\frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ 之所以能够进行压缩，是因为度规张量恰好 $$$$ 需要对下标求偏导，如上面的压缩一样，对相同的标记进行了约分。 $$$$ 因此，给定张量的逆变分量和原始基向量，并希望确定协变分量， $$$$一种方法可能是确定对偶基向量， 如g_{ij} A^j=A_i ，g^{ij} A_i=A^j , g^{ij} A_i=A^j $$