我们的自由思想的数学将从三角形的面积公式开始谈起，将陆续为读者推导出近百个三角形的面积公式，本文先从最常用最基本的公式讲起。

在开始之前，先约定一下与三角形相关的一些量的符号记法，在以后的文章中，在没有特殊说明的情况下，这些记号都是表达相同的意思。

如上图所示，三角形ABC，记a，b，c为三边的长，A，B，C为三个对应的三个内角的大小，R表示外接圆半径，r表示内切圆半径，p表示周长的一半，即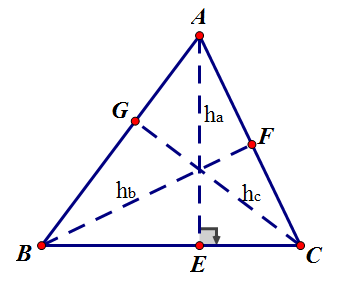，表示其面积，，，表示对应边上的高，，，表示对应边上的中线长，，，表示对应角的角平分线长。

如上面的三角形高线图所示，首先，我们能够想到的三角形面积公式是底乘高的一半，即

我们记为公式一。

公式一在小学的课本上就知道了，它是这么得来的。面积的概念既是数学上的，也是物理上的，其定义大致就是物体所占的平面图形的大小。并定义边长为1的正方形的面积为一个单位面积，以此来衡量其它平面图形的面积大小。因此，很自然地就能知道正方形的面积就是边长的平方，长方形的面积是长乘以宽，平行四边形的面积可以通过割补形成等价的长方形，于是面积就是底乘以高，而两个全等的三角形可以拼成一个平行四边形，于是其面积自然就是底乘以高的一半。

利用三角函数可以将高用边和角的三角函数求出，很明显，，这样就会有

我们记为公式二。

在探讨下一个三角形的面积公式之前，我们顺便证明一下正弦定理。

如上图所示，AD为直径，所以∠ACD=90°，由同弧所对圆周角相等，所以∠B = ∠D，从而有，，同理有，于是就有，这便是正弦定理。

实际上，正弦定理压根底不需要额外的工具来证明，在高中课本里，为了表达向量的作用，使用了向量来证明，其实要得到正弦定理，由公式二便可以直接得到了，因为在推导公式二时，我们已经得到了，所以，所以，同理有：，我们之所以给出上面的证明，目的在于引出其中的几何意义以及三角形外接圆半径R。

三角形的外接圆是由它三条边上的垂直平分线交于一点得来的，并且在初中我们就已经证明了，任何一个三角形都有唯一一个外接圆，这样，外接圆就成了与三角形绑定的一种特性，是三角形几何中必不可少的重要组成元素，直接由它就联系了三角形与圆这两种几何图形。外接圆，以及后面将要说到的内切圆，给我们的启示是：一个事物原本的属性可能会联系着另一个事物的属性，更可能惊奇地发现它们之间存在一种类似于函数的对应关系。如果把三角形看做是自变量，外接圆或者是内切圆看成是因变量，这种对应关系和函数关系一样。我们传统中的函数定义，自变量是数，因变量也是数，那么这种几何图形与几何图形的对应关系，或许可以有一个专业的名词，叫做“泛函”，确切的来说，应该只能用“映射”一词，以免和数学中专业的泛函概念产生误解。学过编程的读者或许知道，在C#、Java中就有泛型这一概念，而“泛”这个字的含义就是广泛、泛化的意思，于是泛型就是可以代表许多类型的意思，而不只是一种类型的变量，那么泛函也就是这个意思，泛函的自变量和因变量理论上可以是任何对象，可以是数，也可以是几何图形，更有可能是函数本身。关于泛函的问题，尤其是几何图形与几何图形之间的对应关系的问题，日后，我们还会在别的文章里详细说明，本文就不再多说了。

将正弦定理带入公式二中，消去 ，则有：

记为公式三。

将正弦定理带入到公式二中，消去a，b，于是有：

记

为公式四。

如上面的三角形ABC内切圆图所示，对三角形ABC进行分割，其面积可以分成三个小三角形面积之和，即：

记

为公式五。

在内切圆图中，有，，，带入公式五中，则有：

记为公式六。

内切圆是由三角形的三条角平分线的交点所得来的，它和外接圆一样是一个三角形唯一的一个属性，因此也就成了与边长和角度一样重要的量。利用内切圆的圆心和圆的半径垂直于切线的性质，将三角形分割为三个可求解面积的小三角形，这种分割法求面积是最常用的求解方法之一，基本思想就是将未知的图形面积转化为已知图形的面积，将大图化小图，将大问题分解为小问题，直到我们可以求解为止，这样的思想并不局限于几何求面积，也不局限与数学问题，在生活中，这都是一个很重要的方法。

对公式五带入正弦定理有：

记为公式七。

利用余弦定理我们可以将角转化为边，由，可以得到

所以

记

为公式八，此式又称为秦九韶公式。

我们对秦九韶公式进行一些变换：

（平方差公式）

当我们遇到三角形三边和与差的问题时，记住这个变形的公式，往往会给解题带来新的思路和便捷。

秦九韶公式还可以经过变换得到一个形式很整齐的公式，叫做海伦公式，形式如下：

即是半周长。我们将此式子记为公式八。

为了完整，我们逆向证明一下这个公式。

由于

由余弦定理，代入上式得：

=

上式结果为公式二，证毕。

将秦九韶公式完全展开整理可得：。

由于三角形就是三条线段所围成的图形，也是平面几何，乃至立体几何中，都是属于最简单的一种封闭图形，因此它的地位可以说是几何的基石。既然三条线段就可以决定了一个三角形的形状（关于三角形形状的确定，我将会在另外的文章里详细说明），那么它的面积自然就一定可以用三条边长来给出，于是秦九韶公式就很自然地成为研究对象了，但是到具体应用的时候，往往需要变形得到新的公式，虽然秦九韶公式和海伦公式本质上是一样的，但是到了具体求解问题时，它们却会有着不同的用途，因此，我们需要有一种变形变通的能力，对应于生活也一样，同一件事物，或者本质一样的事物，其表现形式不同，也会有不同的用处，或者是不同的解决方案。

由公式一和公式二，

于是

记为公式九。

对比公式三和公式五，可以得出，带入上式，便有：

记为公式十。

类似于公式十这样的公式，看起来好像没用，因为其中包含了a、b、c、A、B、C全部的量，若要是知道了这么多的量，面积早就由公式二、公式八得出了，哪里还需要这个？其实不然，公式十表达的意思是：当我们知道了三边的乘积，三边的和，以及三个角的正弦值之和，这三个量时，我们就可以直接求解面积了，而不需要知道边长和角度的具体值。

总结：以上公式所涉及的量都是三角形中最为常用的量，即边长和角度，所推导出的三角形面积公式也是常用的公式，其中公式一、公式二、公式五、公式七最为常用，而公式四和公式六将会在日后的文章里表现出特别的意义。