大学物理复习 |
您所在的位置:网站首页 › 电偶极子受到的电场力 › 大学物理复习 |
大学物理复习
|
静电场
静电场:相对于观察者静止的电场 本章重要概念 一个理想模型:点电荷 一个实验规律:库仑定律 两个物理量:电场强度、电势 两个定理: 高斯定理、环路定理 电荷 库伦定律 电荷引出概念: 电量: 电荷的多少 单位:库伦(C) 物质的电结构物质通过电可以作以下分解 分子-> 原子->原子核(质子,中子)、电子 电荷的量子化效应1909年密立根油滴实验证明了例子的电荷是量子化的在公式上表达为 \[Q=N*e \]其中e为元电荷,其大小为 \[e=1.6*10^{-19}C \]电荷的相对论不变性即在不同的参考系内观察,同一带电粒子的电量不变 电荷守恒定律在电行为中,摩擦起电、静电感应、电荷中和都只是电荷转移,而没有对电荷的总量发生改变 而电子对的淹没:\(e^-+e^+=2\gamma\)在代数和上没有对电荷总量进行更改 因此我们有结论: 在一个孤立系统中,无论发生何种物理过程,该系统电荷的代数和保持不变,这就是电荷守恒定律 这一定律在一切宏观和微观过程中普遍成立 库仑定律库仑定律:真空中两个静止的电荷之间的作用力(静电力),与他们所带的电量的乘积成正比,与他们之间的距离的平方成反比,作用力沿着这两个点电荷的连线 上述定理表现为公式即是 \[\vec F_{21}=\vec F_{12}=k\frac{q_1q_2}{r^2} \vec {r_0} \]其中 \[k=\frac{1}{4\pi \epsilon_0}\approx 9.0*10^9N·m^2·C^{-2} \]\[\epsilon_0=8.85*10^{-12}C^2N^{-1}m^{-2} \]\[\vec {r_0}——单位矢量,由施力物体指向受力物体 \]静电力叠加原理静电力叠加原理:作用于某电荷上的总静电力等于其他点电荷单独作用存在时作用于该电荷的静电力的矢量和 数学上表达为: 离散状态 \[\vec F=\sum^{N}_{i=1}\vec F_i \]\[\vec {F_i}=\frac{qq_i}{4\pi\epsilon_0r_i^2}\vec {r_{i0}} \] 连续分布 \[\vec F=\int d\vec F \]\[d\vec F=\frac{qdq}{4\pi\epsilon_0r^2}\vec {r_0} \]电场强度 电场场:场是物质存在的一种形式,与实物一样具有能量与动量,有自己的运动规律,静质量为0,若干个场可以占据同一空间,场可以相互叠加。电荷之间的作用就是通过场发生的 静电场的对外表现 对放入其中的物体产生电场力作用 对放入其中的导体和电介质产生静电感应作用和极化作用 当带电体在电场中移动时,电场力将对该带电体做功,表明电场具有能量。 电场强度想要探究电场强度需要我们引入试探电荷的概念 试探电荷:带电量足够小,不影响原电场分布,线度小,可视为点电荷的电荷 通过试探电荷我们可以讲电场强度定义为$$\vec E=\frac{\vec F}{q_0}$$ 其中E的大小在数值上等于单位正电荷在该点所受的电场力的大小 方向与该正电荷所受的电场力相同 单位即是牛/库伦 N/C 当场中各点的场强大小方向都相等时,我们就可以称该电场为匀强电场 值得注意的是,通过上述方法测得的电场强度通常比实际的电场强度略小 场强叠加原理与电场力相似,场强也可以进行叠加 点电荷系: \[\vec E=\sum^N_{i=1}\vec {E_i} \]离散带电体: \[\vec E=\int d\vec E \]电场强度计算 点电荷的电场 \[\vec E=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\vec r_0 \] 点电荷系的电场 设真空中有n个点电荷设为\(q_1,q_2...q_n\)则场强为 \[\vec E=\sum_i\vec E_i=\sum_i\frac{1}{4\pi\epsilon_0}\frac{q_i}{r_i^2}\vec {r_{i0}} \]据此我们引出一个重要例题
相加得到 \[\vec E_A=\frac{2qrl}{4\pi\epsilon_0r^4(1-\frac{l}{2r})^2(1+\frac{l}{2r})^2}\vec i \]由于r>>l,因此\(\frac{l}{2r}\approx0\) 令\(ql\vec i=\vec p\) \[\vec E_A=\frac{1}{4\pi\epsilon_0}\frac{2ql}{r^3}\vec i=\frac{1}{4\pi\epsilon_0}\frac{2\vec p}{r^3} \]对B点:\(E_+=E-=\frac{1}{4\pi\epsilon_0}\frac{q}{(r^2+\frac{l^2}{4})}\) \(E_y=0\) \(E_x=2E_{+x}=-2E_+\frac{\frac{l}{2}}{\sqrt{r^2+\frac{l^2}{4}}}\) 与上同 由于r>>l,因此\(\frac{l}{2r}\approx0\) 令\(ql\vec i=\vec p\) \[\vec E_B=-\frac{1}{4\pi\epsilon_0}\frac{\vec p}{r^3} \]
由此 \(\vec E_A ,\vec E_B\)与p成正比,与\(r^3\)成反比,而\(p\)即为电偶极矩 电偶极子是一个重要的物理模型,在研究电介质的极化、电磁波的发射和吸收以及中性分子之间的相互作用等问题时,都要用到该模型。 连续带电体的电场 \[\vec E=\int d\vec E=\frac{1}{4\pi\epsilon_0}\int \frac{dq}{r^2}\vec {r_0} \]其中,电荷元\(dq\)随着不同的电荷分布应该表示为: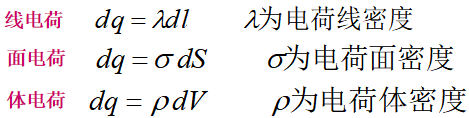 例题分析
例题分析
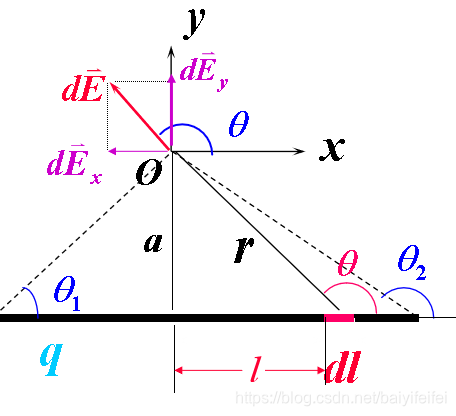
求一均匀带电细直棒在O点的电场。
已知: a 、\(\theta_1\)、\(\theta_2\)、\(\lambda\)。
我们选择以角度\(\theta\)作为积分变量 \[l=\frac{a}{tan(\pi-\theta)}=\frac{a}{-tan\theta} \]\[d l=\frac{a}{(sin\theta)^2}d\theta \]\[r^2=a^2+l^2=\frac{a^2}{(sin\theta)^2} \]那么\(dE=\frac{1}{4\pi\varepsilon_0}\frac{\lambda dl}{r^2}=\frac{\lambda}{4\pi\varepsilon_0a}d\theta\) 据此: \(dE_x=\frac{\lambda}{4\pi\varepsilon_0a}cos\theta d\theta\) \(dE_y=\frac{\lambda}{4\pi\varepsilon_0a}sin\theta d\theta\) 对上述二者进行积分 \(E_x=\int dE_x=\int _{\theta_1} ^{\theta_2}\frac{\lambda}{4\pi\varepsilon_0a}cos\theta d\theta=\frac{\lambda}{4\pi\varepsilon_0a}(sin\theta_2-sin\theta_2)\) \(E_y=\int dE_y=\int_{\theta_1}^{\theta_2}\frac{\lambda}{4\pi\varepsilon_0a}sin\theta d\theta=\frac{\lambda}{4\pi\varepsilon_0a}(cos\theta_1-cos\theta_2)\) \(E=\sqrt{E_x^2+E_y^2}\)方向即为与X夹角为\(arctan\frac{E_y}{E_x}\) 当直线无限长时,\(E_x=0,E=E_y=\frac{\lambda}{2\pi\varepsilon_0a}\) 由此得出推论: 无限长均匀带电直线的场强\(E=\frac{\lambda}{2\pi\varepsilon_0a}\)
求一均匀带电圆环轴线上任一点 x处的电场。
已知: q 、a 、 x。
求均匀带电半圆环圆心处的 ,已知 R、\(\lambda\)
求均匀带电细圆弧圆心处的场强,已知\(\alpha,\lambda,\)R
求均匀带电圆盘轴线上任一点的电场。 已知:q、 R、 x 求:Ep
由上,当R>>x时,\(E=\frac{\sigma}{2\varepsilon_0}\),R0$$表明电力线从正电荷发出,穿出闭合曲面,所以**正电荷是静电场的源头**$$\sum q_i>l\) \(\therefore r_2-r_1\approx lcos\theta,r_1r_2\approx r^2\) \(\therefore u=\frac{q}{4\pi\varepsilon_0}\frac{lcos\theta}{r^2}\) \(\because r=\sqrt{x^2+y^2},cos\theta =\frac{x}{r}\) \[u=\frac{1}{4\pi\varepsilon_0}\frac{px}{(x^2+y^2)^\frac{3}{2}} \]求均匀带电圆环轴线上的电势分布。已知:R、q
求均匀带电球面电场中电势的分布,已知R,q
|
【本文地址】
今日新闻 |
推荐新闻 |
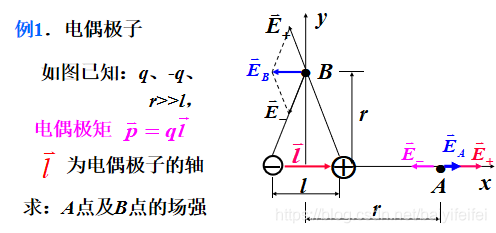 解:对于A点 我们可以设+q与-q的场强大小分别为\(\vec E_+ 和\vec E_-\)
解:对于A点 我们可以设+q与-q的场强大小分别为\(\vec E_+ 和\vec E_-\)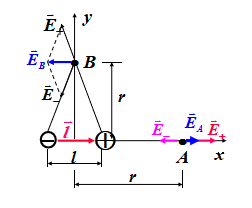
 \(dE=\frac{dq}{4\pi\varepsilon_0(L-X+a)^2}\)
\(E=\int_{0}^{L}\frac{\lambda dx}{4\pi\varepsilon_0(L-X+a)^2}=\frac{\lambda}{4\pi\varepsilon_0}(\frac{1}{a}-\frac{1}{L+a})=\frac{q}{4\pi\varepsilon_0a(L+a)}\)
\(dE=\frac{dq}{4\pi\varepsilon_0(L-X+a)^2}\)
\(E=\int_{0}^{L}\frac{\lambda dx}{4\pi\varepsilon_0(L-X+a)^2}=\frac{\lambda}{4\pi\varepsilon_0}(\frac{1}{a}-\frac{1}{L+a})=\frac{q}{4\pi\varepsilon_0a(L+a)}\)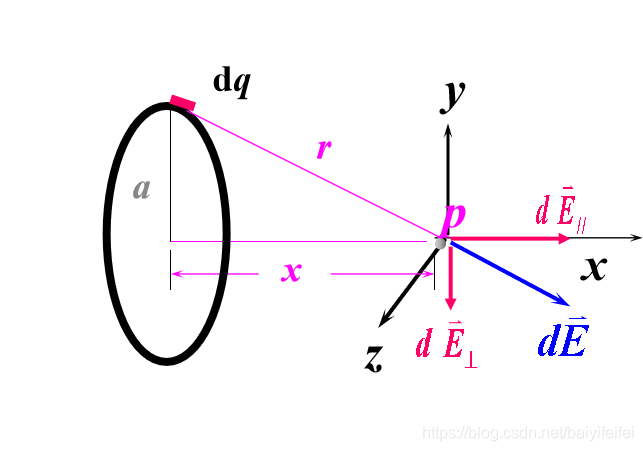 \(dq=\lambda dl\)
\(\lambda=\frac{q}{2\pi r}\)
\(dE=\frac{dq}{4\pi\varepsilon_0r^2}\)
据对称性\(E_x=\int \frac{x}{r}d\vec E\)
因此\(E=\oint_{2\pi a}\frac{1}{4\pi\varepsilon_0}\frac{q}{2\pi a}\frac{x}{r^3}dl=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^3}x=\frac{1}{4\pi\varepsilon_0}\frac{qx}{(x^2+a^2)^{\frac{3}{2}}}\)
\(dq=\lambda dl\)
\(\lambda=\frac{q}{2\pi r}\)
\(dE=\frac{dq}{4\pi\varepsilon_0r^2}\)
据对称性\(E_x=\int \frac{x}{r}d\vec E\)
因此\(E=\oint_{2\pi a}\frac{1}{4\pi\varepsilon_0}\frac{q}{2\pi a}\frac{x}{r^3}dl=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^3}x=\frac{1}{4\pi\varepsilon_0}\frac{qx}{(x^2+a^2)^{\frac{3}{2}}}\)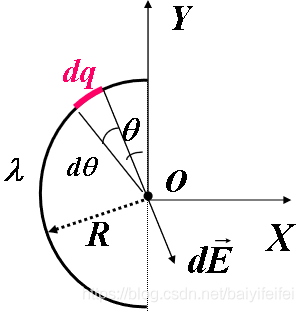 \(dE=\frac{dq}{4\pi\varepsilon_0R^2}\)
\(q=\lambda Rd\theta\)
据对称性
\(E=\int_0^\pi \frac{\lambda Rd\theta}{4\pi\varepsilon_0R^2}sin\theta=\frac{\lambda}{2\pi\varepsilon_0R}\)
\(dE=\frac{dq}{4\pi\varepsilon_0R^2}\)
\(q=\lambda Rd\theta\)
据对称性
\(E=\int_0^\pi \frac{\lambda Rd\theta}{4\pi\varepsilon_0R^2}sin\theta=\frac{\lambda}{2\pi\varepsilon_0R}\)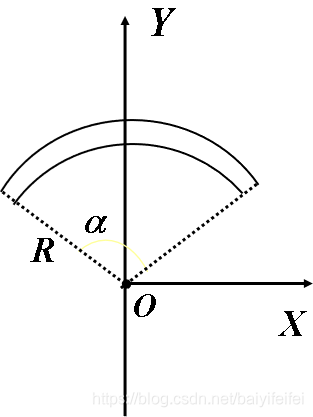 与上题同理,只是积分区域不同
\(E=\int dE_y=2\int_0^\frac{\alpha}{2} \frac{\lambda Rd\theta}{4\pi\varepsilon_0R^2}cos\theta=\frac{\lambda}{2\pi\varepsilon_0R}sin\frac{\alpha}{2}\)
与上题同理,只是积分区域不同
\(E=\int dE_y=2\int_0^\frac{\alpha}{2} \frac{\lambda Rd\theta}{4\pi\varepsilon_0R^2}cos\theta=\frac{\lambda}{2\pi\varepsilon_0R}sin\frac{\alpha}{2}\)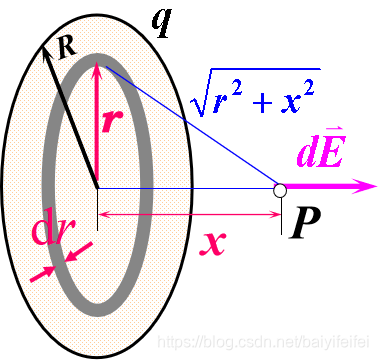 \(dq=\sigma d\pi r^2=\sigma2\pi rdr\)
\(\sigma=\frac{q}{\pi R^2}\)
因为圆环产生的电场强度为:\(\frac{1}{4\pi\varepsilon_0}\frac{qx}{(x^2+a^2)^{\frac{3}{2}}}\)
\(dE=\frac{1}{4\pi\varepsilon_0}\frac{xdq}{(x^2+a^2)^{\frac{3}{2}}}=\frac{x\sigma^22\pi rdr}{4\pi\varepsilon_0(r^2+x^2)^{\frac{3}{2}}}\)
\(E=\int dE=\int_0^R \frac{\sigma x}{2\varepsilon_0}\frac{rdr}{(r^2+x^2)^{\frac{3}{2}}}=\frac{\sigma}{2\varepsilon_0}(1-\frac{x}{\sqrt{R^2+x^2}})\)
\(dq=\sigma d\pi r^2=\sigma2\pi rdr\)
\(\sigma=\frac{q}{\pi R^2}\)
因为圆环产生的电场强度为:\(\frac{1}{4\pi\varepsilon_0}\frac{qx}{(x^2+a^2)^{\frac{3}{2}}}\)
\(dE=\frac{1}{4\pi\varepsilon_0}\frac{xdq}{(x^2+a^2)^{\frac{3}{2}}}=\frac{x\sigma^22\pi rdr}{4\pi\varepsilon_0(r^2+x^2)^{\frac{3}{2}}}\)
\(E=\int dE=\int_0^R \frac{\sigma x}{2\varepsilon_0}\frac{rdr}{(r^2+x^2)^{\frac{3}{2}}}=\frac{\sigma}{2\varepsilon_0}(1-\frac{x}{\sqrt{R^2+x^2}})\)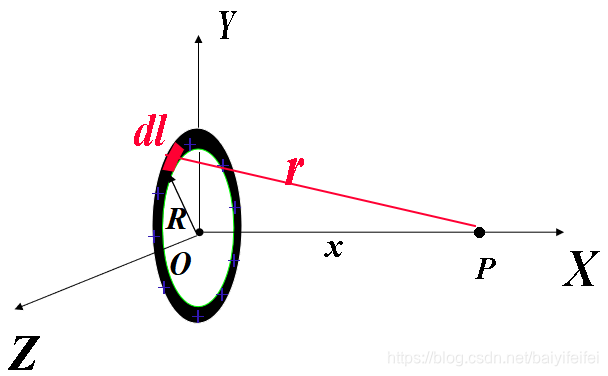 Solution 1
\(du=\frac{dq}{4\pi\varepsilon_0r}\)
\(u_p=\int du=\int _0^{2\pi R}\frac{\lambda dl}{4\pi\varepsilon_0r}=\frac{q}{4\pi \varepsilon_0\sqrt{R^2+x^2}}\)
Solution 2
\(E=\frac{qx}{4\pi\varepsilon_0(x^2+R^2)^{\frac{3}{2}}}\)
\(u=\int_{x_p}^{\infty}Edx=\frac{q}{4\pi \varepsilon_0\sqrt{R^2+x^2}}\)
Solution 1
\(du=\frac{dq}{4\pi\varepsilon_0r}\)
\(u_p=\int du=\int _0^{2\pi R}\frac{\lambda dl}{4\pi\varepsilon_0r}=\frac{q}{4\pi \varepsilon_0\sqrt{R^2+x^2}}\)
Solution 2
\(E=\frac{qx}{4\pi\varepsilon_0(x^2+R^2)^{\frac{3}{2}}}\)
\(u=\int_{x_p}^{\infty}Edx=\frac{q}{4\pi \varepsilon_0\sqrt{R^2+x^2}}\)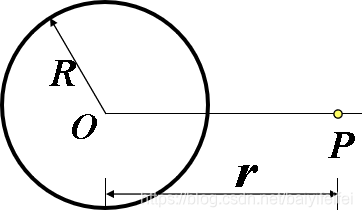 由高斯定理求出场强分布为$$\vec E=\begin{cases}\frac{q\vec {r_0}}{4\pi\varepsilon_0r^2}&r>R\0&r
由高斯定理求出场强分布为$$\vec E=\begin{cases}\frac{q\vec {r_0}}{4\pi\varepsilon_0r^2}&r>R\0&r