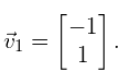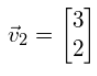搞懂特征值与特征向量 |
您所在的位置:网站首页 › 特征向量可以随便取吗 › 搞懂特征值与特征向量 |
搞懂特征值与特征向量
|
文章目录
简述定义例子加深理解阐述
简述
首先明确特征值和特征向量是对谁而言的呢, 是对一个变换矩阵而言的, 特征值表示变换矩阵能起到多大作用, 特征值越大代表对应的变化程度越剧烈, 那么具体是变化谁呢? 就是变换的特征向量.也就是说, 特征值是用来衡量变换矩阵对特征向量的变换程度
定义
A A A为 n ∗ n n*n n∗n的矩阵, x x x为非零向量,若存在数λ使 A x = λ x Ax=λx Ax=λx有非平凡解 x x x,则称 λ λ λ为 A A A的特征值, x x x称为对应于 λ λ λ的特征向量 举个例子: 设:
可以看到A对特征向量的作用是很简单的,它只是对特征向量进行了拉伸,而特征值表达了它拉伸的方向和大小 用数学式子表达, 就是这样的: A x = λ x Ax = \lambda x Ax=λx 变换一下位置, 即: ( A − λ I ) x = 0 (A-\lambda I)x=0 (A−λI)x=0 假定这里x不是空向量,等式只能在 ( A − λ I ) (A-\lambda I) (A−λI)不可逆的时候才能被定义。如果一个方阵是不可逆的,这意味着它的行列式必须等于零。因此,要找到A的特征向量,我们只需要解决以下公式: D e t ( A − λ I ) = 0 Det(A-\lambda I)=0 Det(A−λI)=0 例子加深理解假设存在一个变换矩阵A: 计算特征向量 根据公式
A
x
=
λ
x
Ax = \lambda x
Ax=λx, 我们知道: 对于这个例子,我们随意地选择 x 12 x_{12} x12 = 1,使得 x 11 x_{11} x11= -1。因此,对应于特征值λ值为-1的特征向量是
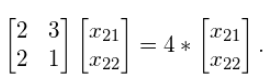 用
x
21
x_{21}
x21的函数式解决第一个等式得到: 用
x
21
x_{21}
x21的函数式解决第一个等式得到: 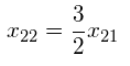
然后,我们随意地选择
x
21
x_{21}
x21 = 2,并发现
x
22
x_{22}
x22= 3。因此,对应于特征值
λ
2
λ_2
λ2= 4的特征向量是: 至此变换矩阵A的特征值和特征向量就求解结束了 阐述 假如有个高维度的变换矩阵A, 我们不想直接使用它, 而是想用另外的方式保存它, 那么我们就可以选择它的特征向量和特征值, 我们就能复原出它对应的变换来我们还知道特征值的大小对应的变换的程度, 我们就可以丢弃小的特征值对应的特征向量, 保留大的, 这不就是降维了吗? |
【本文地址】
今日新闻 |
推荐新闻 |
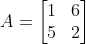
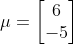
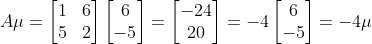
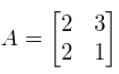 根据公式
(
A
−
λ
I
)
x
=
0
(A-\lambda I)x=0
(A−λI)x=0, 我们知道:
根据公式
(
A
−
λ
I
)
x
=
0
(A-\lambda I)x=0
(A−λI)x=0, 我们知道: 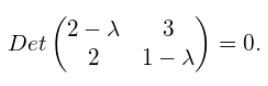 可求得:
可求得: 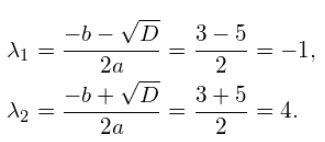 现在我们已经确定了两个特征值λ1和λ2。需要注意的是大小为NxN的方阵总是具有N个特征值,每一个对应一个特征向量。特征值用来求特征向量
现在我们已经确定了两个特征值λ1和λ2。需要注意的是大小为NxN的方阵总是具有N个特征值,每一个对应一个特征向量。特征值用来求特征向量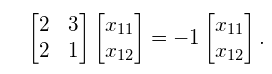 由于这仅仅是方程组的矩阵符号,我们可以写出它的等价形式:
由于这仅仅是方程组的矩阵符号,我们可以写出它的等价形式: 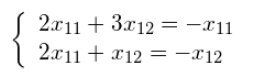 并用
x
12
x_{12}
x12的一个函数解决了第一个等式:
并用
x
12
x_{12}
x12的一个函数解决了第一个等式: 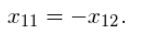 因为特征向量仅仅代表一个方向(相应特征值表示幅度),特征向量的所有标量倍数是平行于该特征向量的向量,因此它们是等效的(如果我们标准化向量,它们将是相等的)。因此,进一步求解上面的方程组,我们可以自由地选择
x
11
x_{11}
x11或
x
12
x_{12}
x12的真实值,并用等式来确定另一个。
因为特征向量仅仅代表一个方向(相应特征值表示幅度),特征向量的所有标量倍数是平行于该特征向量的向量,因此它们是等效的(如果我们标准化向量,它们将是相等的)。因此,进一步求解上面的方程组,我们可以自由地选择
x
11
x_{11}
x11或
x
12
x_{12}
x12的真实值,并用等式来确定另一个。