仕事と力学的エネルギー |
您所在的位置:网站首页 › 物理p的公式力学 › 仕事と力学的エネルギー |
仕事と力学的エネルギー
|
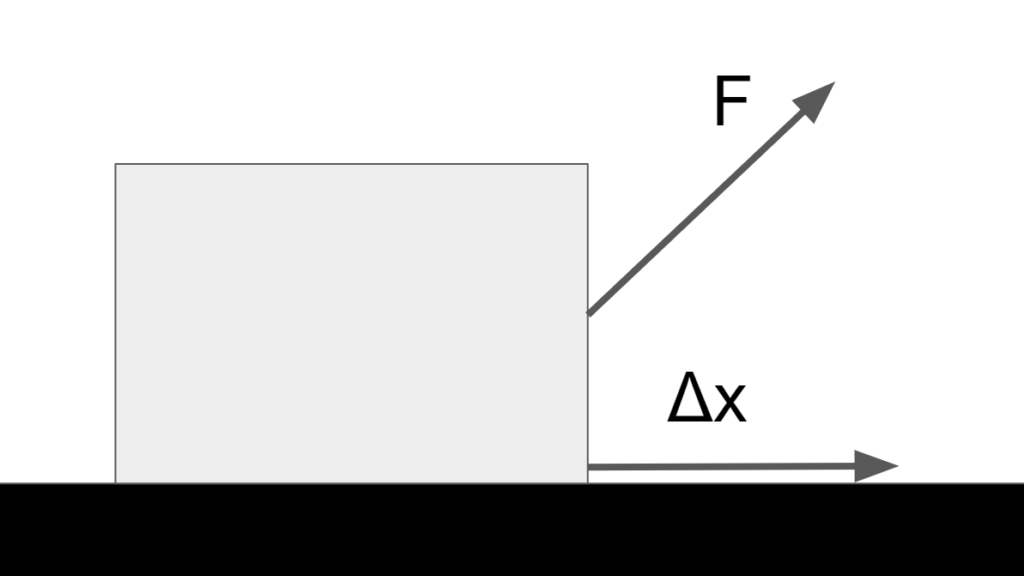
エネルギーとは、物体が持つ物理量の一つである。 エネルギーには様々な種類があるが、それらのエネルギーの総和は一定である。(エネルギー保存則) 人間は様々なエネルギーを扱うことで自動車を動かしたり、テレビを見たりすることができる。 エネルギーの中でも物体の運動に関係する力学的エネルギーについて本記事では説明する。 運動している物体は速度を持ったり、重力由来の高さ方向のエネルギーを持つ。 これらのエネルギーは物体に仕事をする(物体にエネルギーを与える)ことで物体のエネルギーを変化させて、物体の運動を変えることができる。 物体の持つエネルギーと、そのエネルギーを変化させる仕事について理解することが重要である。 Contents 仕事力学的エネルギー運動エネルギー位置エネルギー弾性エネルギー力学的エネルギー保存則仕事物体に加えた力\(\overrightarrow{F}\)によって物体が\(\Delta\overrightarrow{x}\)だけ移動した時の力\(\overrightarrow{F}\)がした仕事\(W\)は以下になる。 \begin{eqnarray} W=\overrightarrow{F}\cdot\Delta\overrightarrow{x} \end{eqnarray} これは、\(\overrightarrow{F}\)と\(\Delta\overrightarrow{x}\)の内積である。
また、力\(\overrightarrow{F}\)が単位時間あたりにする仕事を仕事率\(P\)と呼び、以下になる。 \begin{eqnarray} P&=&\frac{W}{\Delta t}=\frac{\overrightarrow{F}\cdot\Delta\overrightarrow{x}}{\Delta t}=\overrightarrow{F}\cdot\overrightarrow{v}\\ \\ \Delta t&:&力を加えた時間\\ \overrightarrow{v}&:&\Delta tの間に進んだ距離(速度) \end{eqnarray} これは、力\(\overrightarrow{F}\)と物体の速度\(\overrightarrow{v}\)の内積である。 【ベクトルの内積とは】 力学的エネルギー 運動エネルギー運動エネルギーとは物体が運動をしている(速度を持つ)時に持つエネルギーのことである。 物体が運動している時の運動エネルギー\(K\)は以下である。 \begin{eqnarray} K&=&\frac{1}{2}mv^2\\ \\ m&:&質量\\ v&:&速度 \end{eqnarray} この運動エネルギー\(K\)は運動量から物体にかかる仕事を求めることで分かる。 まず、力とは運動量の時間変化である。 よって、力\(F\)は以下のように表せる。 \begin{eqnarray} F&=&\frac{d}{dt}\left(mv\right)\\ \\ &=&m\frac{dv}{dt}\\ \\ v&:&速度 \end{eqnarray} この時、物体が微小な時間\(dt\)の間に進んだ距離は\(vdt\)である。 よって、力\(F\)が微小な時間\(dt\)の間に物体に与えた仕事\(dW\)は力と進んだ距離の積で表すので以下になる。 \begin{eqnarray} dW=m\frac{dv}{dt}vdt\\ \\ =mvdv \end{eqnarray} この微小な仕事\(dW\)を積分すると以下になる。 \begin{eqnarray} \int dW&=&\int mvdv\\ \\ &=&\frac{1}{2}mv^2 \end{eqnarray} よって、力\(F\)が物体にした仕事が運動エネルギーとして変換し、物体は運動をするのである。 【運動量とは】 位置エネルギー位置エネルギー\(U\)とは任意の基準面(鉛直方向)から距離\(h\)だけ離れた時に物体が持つエネルギーであり、以下のように表せる。 \begin{eqnarray} U&=&mgh\\ \\ m&:&質量\\ g&:&重力加速度\\ \end{eqnarray}
ここで、積分を基準面\(y=y_0\)から\(y=h\)まで積分すると以下になる。 \begin{eqnarray} U=mgh-mgy_0 \end{eqnarray} この時、基準面を\(y_0=0\)とするとポテンシャル\(U\)は\(mgh\)となることが分かる。 基準面\(y_0=0\)とした理由は、位置エネルギーを考える時は自由に基準面(つまり、位置エネルギーが0になる高さ)を決めていよいからである。 位置エネルギーを考える時に重要なのは高さ\(A\)から高さ\(B\)まで変化した時の位置エネルギーの変化量である。 なので、位置エネルギーの変化に注目すれば、どの高さを基準面としても良い事が分かる。 【積分の方法】 弾性エネルギーバネを自然長から\(\Delta x\)だけ縮めた(もしくは伸ばした)時、バネにエネルギー\(U_k\)が蓄えられる。 このエネルギー\(U_k\)を弾性エネルギーと呼び、以下で表す。 \begin{eqnarray} U_k=\frac{1}{2}k\left(\Delta x\right)^2\\ \\ k:バネ定数 \end{eqnarray} 弾性エネルギーはバネの弾性力が作り出すポテンシャルである。 ポテンシャル\(U_k\)は以下で定義する。 \begin{eqnarray} U_k=-\int\underbrace{-kx}_{弾性力}dx’ \end{eqnarray} この積分をバネの自然長\(x_0\)から変形量\(\Delta x\)まで積分する。 \begin{eqnarray} U_k=\frac{1}{2}k\left(\Delta x\right)^2-\frac{1}{2}kx_0^2 \end{eqnarray} ここで、バネの長さが自然長\(x_0\)の時、弾性力は0であるので、以下を満たす。 \begin{eqnarray} \frac{1}{2}kx_0^2=0 \end{eqnarray} よって、弾性エネルギーは\(U_k=\frac{1}{2}k\left(\Delta x\right)^2\)となる。 【バネの弾性力とは】 力学的エネルギー保存則物体が運動をしている時、外力が与えられない時は、力学的エネルギー(運動エネルギー、位置エネルギー、弾性エネルギー)の総量は変わらない。 つまり、式で表すと以下になる。 \begin{eqnarray} K+U+U_k&=&K’+U’+U’_k\\ \\ K,K’&:&t=t_1,t_2の時の運動エネルギー\\ U,U’&:&t=t_1,t_2の時の運動エネルギー\\ U_k,U’_k&:&t=t_1,t_2の時の弾性エネルギー\\ \end{eqnarray} また、物体に力\(F\)を与えて運動した時は、その力が物体にした仕事\(W\)だけ物体の力学的エネルギーに加えられる。 \begin{eqnarray} K+U+U_k+W&=&K’+U’+U’_k\\ \\ K,K’&:&t=t_1,t_2の時の運動エネルギー\\ U,U’&:&t=t_1,t_2の時の運動エネルギー\\ U_k,U’_k&:&t=t_1,t_2の時の弾性エネルギー\\ W&:&力Fが物体にした仕事 \end{eqnarray} |
【本文地址】
今日新闻 |
推荐新闻 |
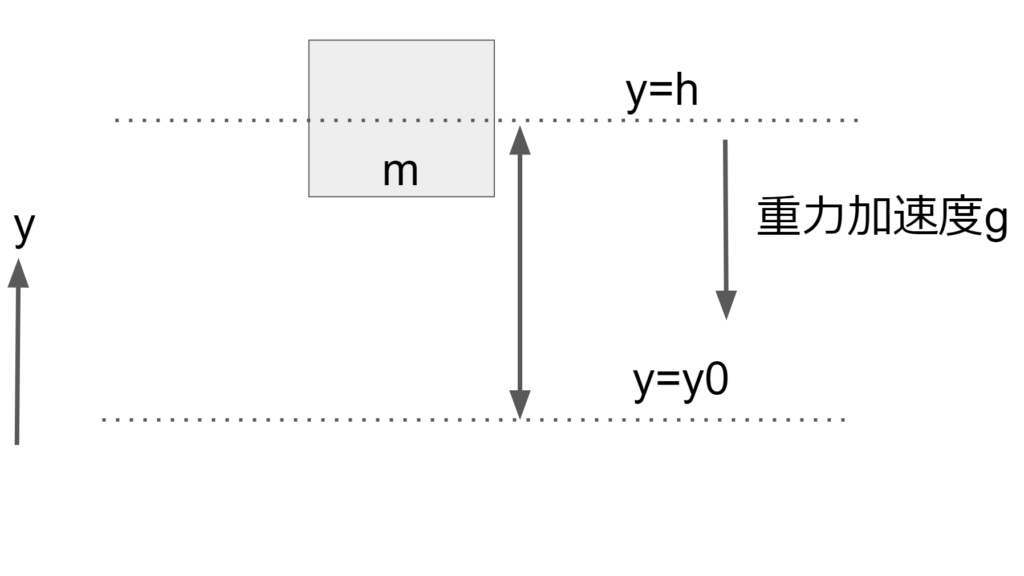 位置エネルギーとは重力が作り出すポテンシャルのことである。
重力は地球上では常に物体に働く。
ポテンシャル\(U\)は以下で定義する。
\begin{eqnarray}
U&=&-\int m\overrightarrow{g}\cdot d\overrightarrow{y}\\
\\
\overrightarrow{g}&:&重力加速度のベクトル\\
\overrightarrow{y}&:&鉛直方向の位置ベクトル
\end{eqnarray}
ここで、\(m\overrightarrow{g}\cdot d\overrightarrow{y}\)は重力による微小な鉛直方向の位置\(d\overrightarrow{y}\)だけ移動させた時の仕事である。
この内積は鉛直方向上向きを正とすると\(m\overrightarrow{g}\cdot d\overrightarrow{y}=-mgdy\)となる。
位置エネルギーとは重力が作り出すポテンシャルのことである。
重力は地球上では常に物体に働く。
ポテンシャル\(U\)は以下で定義する。
\begin{eqnarray}
U&=&-\int m\overrightarrow{g}\cdot d\overrightarrow{y}\\
\\
\overrightarrow{g}&:&重力加速度のベクトル\\
\overrightarrow{y}&:&鉛直方向の位置ベクトル
\end{eqnarray}
ここで、\(m\overrightarrow{g}\cdot d\overrightarrow{y}\)は重力による微小な鉛直方向の位置\(d\overrightarrow{y}\)だけ移動させた時の仕事である。
この内積は鉛直方向上向きを正とすると\(m\overrightarrow{g}\cdot d\overrightarrow{y}=-mgdy\)となる。