用Mathematica 画常微分方程斜率场(积分曲线) |
您所在的位置:网站首页 › 物理ax图像的斜率 › 用Mathematica 画常微分方程斜率场(积分曲线) |
用Mathematica 画常微分方程斜率场(积分曲线)
|
因为最近在看微分方程,想观察一下方程的斜率场,所以就想看看万能的Mathematica能不能画出微分方程的斜率场。百度了一下和自己也查看了一下Mathematica的官方文档,但是发现好像并没有想要的结果,网上找到很多都是先解出微分方程的解,然后再把解导入来画斜率场的。(好像Matlab可以,不过我没用过) 所以就在想有没有方法不用解微分方程,直接用微分方程作输入来画它的斜率场的方法。然后今天下课的时候回宿舍搞了一下,发现可行。所以下面就来跟大家分享一下。 理论分析首先要来的就是先做个理论的分析,来看看从理论上是否可行(该方法只对一阶常微分方程有效) 对于一阶常微分方程有 dydx=f(x,y) 熟悉微分方程的人可能已经对上面方程的几何意义非常熟悉了,左边即斜率,右端为定义在二维平面 R2 上的函数。几何意义非常明显,即 dydx=f(x0,y0) 其中 (x0,y0)∈R2 ,因为上方程左端就是斜率,上面的一阶微分方程即确定了在平面 R2 某点的斜率。所以明显我们可以按照这样在平面上画出该方程的斜率场,而且满足斜率场的其中一条曲线也就是该微分方程的一个特解。 转化为Mathematica语言下面就要把理论上的东西转化为实际在Mathematica上操作的语言。 我们通过查看Mathematica的官方文档,可以知道可以用来画向量场的函数有 StreamPlot[] 和 VectorPlot[] 两个,其中两个的差别只是一个是画流线,一个是画向量箭头的。现在开始在文章下面一直都是使用 StreamPlot[] 来进行画向量场。 不过现在有一个问题是,这两个函数的输入都是分开的,就是只接受输入向量x分量的函数,和y分量的函数,并不是单纯的接受微分方程的输入。而我们从微分方程里面知道的信息只有在某点的斜率,我们要把这个斜率的信息转化成向量的x分量,和y分量的信息。 所以请看下图 到目前为止就完成了从斜率角到向量x跟y方向分量函数的转化,利用计算机上面这个看似复杂,看到头大的公式也能很轻易的计算出来。 测试下面就把上面推出来的x和y方向的函数再Mathematica里面定义 In[1]= fx[z_] := Cos[ArcTan[z]] In[2]= fy[z_] := Sin[ArcTan[z]] 然后定义完了之后,直接就可以调用StreamPlot[]来画斜率场了 In[3]= StreamPlot[{fx[z]], fy[z]}, {x, 0, 10}, {y, -5, 10}] 上面的Mathematica代码,后面两个花括号代表画的范围,前面的花括号代表x的分量函数,和y的分量函数。分量函数里面的z可以替换成你想要求斜率场的微分方程的右端函数。 下面以微分方程 dydx=y2 为例子做一个测试,在Mathematica里面输入如下代码 StreamPlot[{fx[y^2], fy[ y^2]}, {x, 0, 10}, {y, -5, 5}] 我们都知道该微分方程的通解为 y=1c−t 由Mathematica得到斜率场如下图: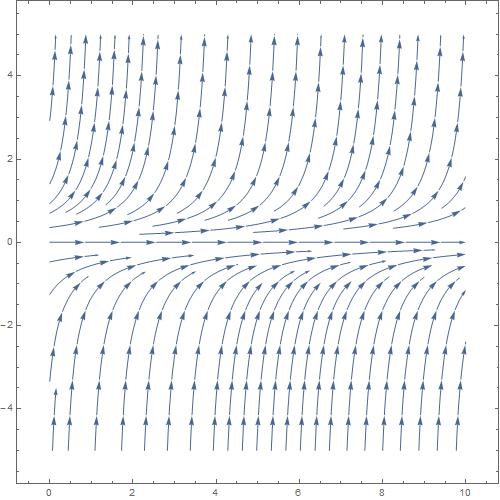 加上斜率向量的大小
加上斜率向量的大小
上面所做的都是在斜率向量的大小为单位长度的情况下做的,下面就来为斜率向量加上随角度大小变化而变化的长度。即斜率向量的大小是斜率角 θ 的函数。 |v⃗ |=|Arctan(f(x,y))| 那么上面推导出的x和y方向的函数,可以写为 |v⃗ x|=|Arctan(f(x,y))|∗cos(Arctan(f(x,y))) 对于y方向同样有 |v⃗ y|=|Arctan(f(x,y))|∗sin(Arctan(f(x,y))) 跟之前的公式一样这看起来很复杂的公式在计算机面前,根本不算什么。非常快就能够算出答案。 那么现在的斜率场就具有了随角度大小变化的向量大小了。 这也能在Mathematica里面体现出来,我们可以设置一个参数来使Mathematica根据向量的大小(范数)来着色,使斜率场更加直观,好看。 着色的代码如下 StreamPlot[{fx[y^2], fy[ y^2]}, {x, 0, 10}, {y, -5, 5}, StreamColorFunction -> Hue] 可以看到在上面的代码里面,设置了一个参数StreamColorFunction->Hue,这个参数代表根据向量的大小来着色。 如下图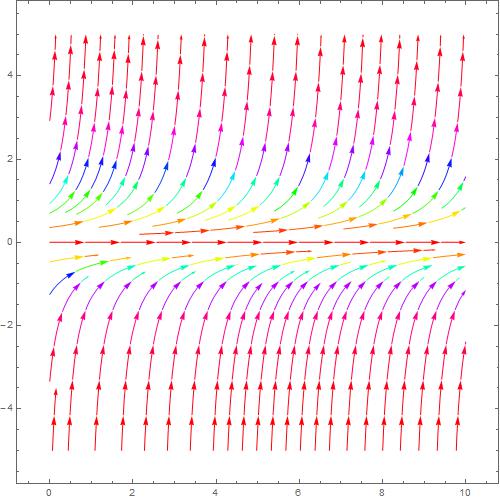 其他方程的斜率场
其他方程的斜率场
好的,用Mathematica画斜率场就到这里了。下面给大家看一下一些我个人认为很漂亮的微分方程的斜率场线
喜欢我们的内容吗?喜欢的话可以关注我们的公众号,扫下面的二维码关注我们吧 |
【本文地址】
今日新闻 |
推荐新闻 |
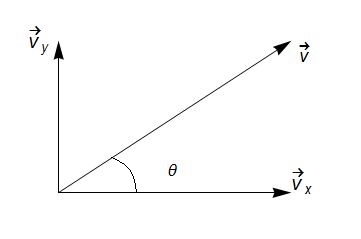 从上图我们看出,假设存在一向量,必有x跟y方向的分量有关系式
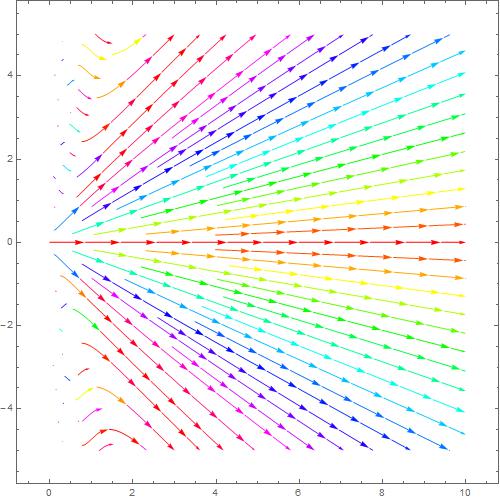
从上图我们看出,假设存在一向量,必有x跟y方向的分量有关系式 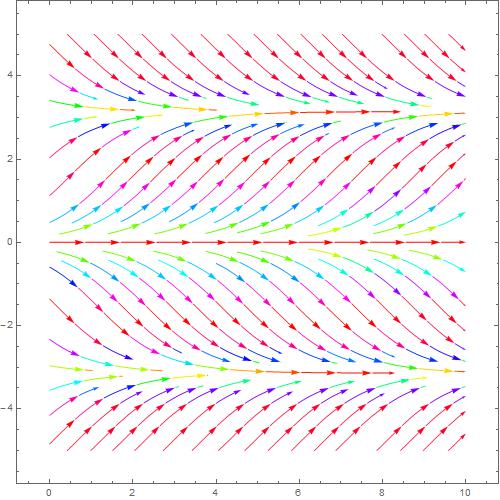 上图是方程
dydx=sin(y)
上图是方程
dydx=sin(y)
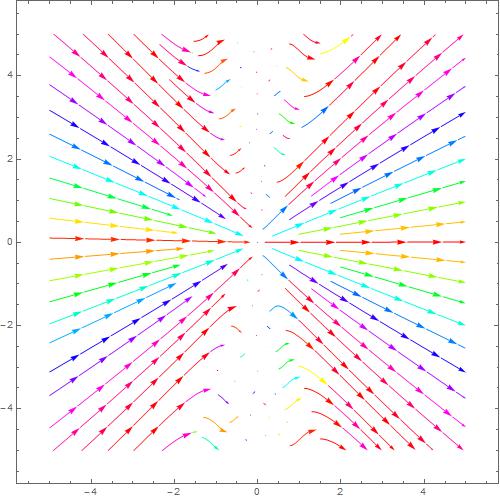 上图是方程
dydx=sin(yx)
上图是方程
dydx=sin(yx)
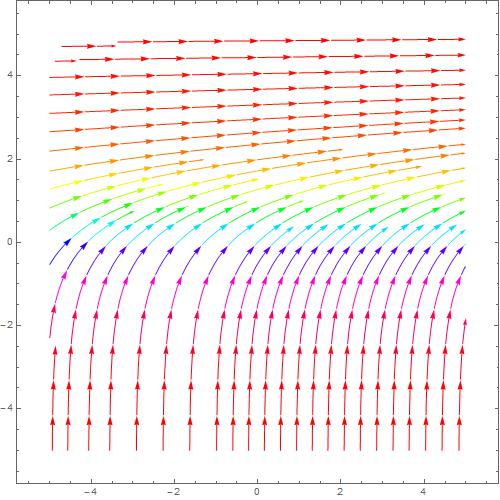 上图是方程
dydx=e−y
上图是方程
dydx=e−y
