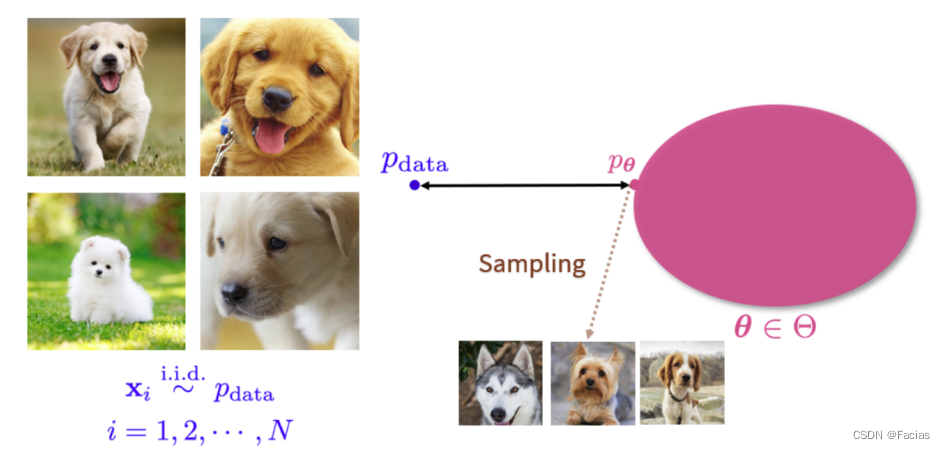
本文章旨在梳理DDPM这篇论文中的各个公式含义及推导，很多内容从其他博客处摘录，在文后列举。一篇文章发不全，拆开成两篇了。

打个比方，就像是给你一块木头，让你把它雕刻成一个佛像，需要栩栩如生。Diffusion model在推理阶段就是在执行逆扩散过程，也就是雕刻佛像的过程。

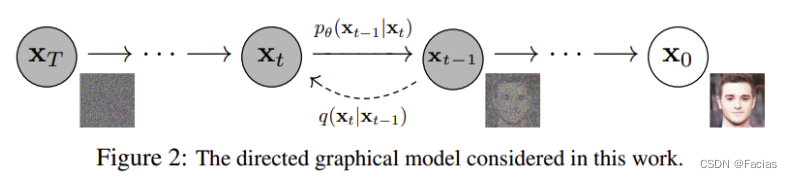
用数学语言进行描述，生成式模型本质上是从一组概率分布中得到另一组概率分布。如下图所示，左边是一个训练数据集，里面所有的数据都是从某个数据 p data  p_{\text {data }} pdata ​中独立同分布取出的随机样本。右边就是其生成式模型（概率分布），在这种概率分布中，找出一个分布 p θ p_ {\theta } pθ​使得它离 p data  p_{\text {data }} pdata ​的距离最近。接着在 p θ p_ {\theta } pθ​上采新的样本，可以获得源源不断的新数据。 Diffusion model由 p data  p_{\text {data }} pdata ​得到 p θ p_ {\theta } pθ​的过程分为两个阶段：

扩散过程 q q q，在 p data  p_{\text {data }} pdata ​上不断加噪声，使得他最终变成一个纯噪声分布 N ( 0 , I ) \mathcal{N}\left(0, I\right) N(0,I)

逆扩散过程 p p p，将噪声 N ( 0 , I ) \mathcal{N}\left(0, I\right) N(0,I)分布逐步地去噪以映射到 p data  p_{\text {data }} pdata ​，有了这样的映射，我们从噪声分布中采样，最终可以得到一张想要的图像，也就是可以做生成了。

而从单个图像样本来看这个过程，扩散过程 q q q就是不断往图像上加噪声直到图像变成一个纯噪声，逆扩散过程 p p p就是从纯噪声生成一张图像的过程。

给定真实图片样本 x 0 ∼ q ( x ) x_{0} \sim q(x) x0​∼q(x)，diffusion 前向过程通过 T T T次累计对其添加高斯噪声，得到 x 1 , x 2 , … , x T x_{1}, x_{2}, \ldots, x_{T} x1​,x2​,…,xT​，如下图的 q q q过程。每一步的大小是由一系列的高斯分布方差的超参数 { β t ∈ ( 0 , 1 ) } t = 1 T \left\{\beta_{t} \in(0,1)\right\}_{t=1}^{T} {βt​∈(0,1)}t=1T​来控制的。 前向过程由于每个时刻 t t t只与 t − 1 t-1 t−1时刻有关，所以也可以看做马尔科夫过程： q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) , q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q\left(x_{t} \mid x_{t-1}\right)=\mathcal{N}\left(x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathbf{I}\right), q\left(x_{1: T} \mid x_{0}\right)=\prod_{t=1}^{T} q\left(x_{t} \mid x_{t-1}\right) q(xt​∣xt−1​)=N(xt​;1−βt​ ​xt−1​,βt​I),q(x1:T​∣x0​)=t=1∏T​q(xt​∣xt−1​)

这个过程中，随着 t t t的增大， x t x_t xt​越来越接近纯噪声。当 T → ∞ T \rightarrow \infty T→∞， x T x_T xT​是完全的高斯噪声（下面会证明，且与均值系数 1 − β t \sqrt{1-\beta_{t}} 1−βt​ ​的选择有关）。

将其中的第 t t t 步提取出来解析， x t x_t xt​的分布为 q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q\left(x_{t} \mid x_{t-1}\right)=\mathcal{N}\left(x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathbf{I}\right) q(xt​∣xt−1​)=N(xt​;1−βt​ ​xt−1​,βt​I)，而 x t − 1 x_{t-1} xt−1​在该步中为已知，即已经被第 t − 1 t-1 t−1步求解出来了，所以 x t − 1 x_{t-1} xt−1​ 可以看作常数。所以 x t x_t xt​ 的均值为常数 1 − β t x t − 1 \sqrt{1-\beta_{t}} x_{t-1} 1−βt​ ​xt−1​ ，方差为 β t \beta_{t} βt​

如果要从高斯分布 z ∼ N ( z ; μ θ , σ θ 2 I ) z \sim \mathcal{N}\left(z ; \mu_{\theta}, \sigma_{\theta}^{2} \mathbf{I}\right) z∼N(z;μθ​,σθ2​I) 采样一个 z z z ，我们可以写成: z = μ θ + σ θ ⊙ ϵ , ϵ ∼ N ( 0 , I ) z=\mu_{\theta}+\sigma_{\theta} \odot \epsilon, \epsilon \sim \mathcal{N}(0, \mathbf{I}) z=μθ​+σθ​⊙ϵ,ϵ∼N(0,I) 所以 q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q\left(x_{t} \mid x_{t-1}\right)=\mathcal{N}\left(x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathbf{I}\right) q(xt​∣xt−1​)=N(xt​;1−βt​ ​xt−1​,βt​I) 可以写作： x t = α t x t − 1 + 1 − α t ϵ t − 1 \mathbf{x}_{t}=\sqrt{\alpha_{t}} \mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1} xt​=αt​ ​xt−1​+1−αt​ ​ϵt−1​ 其中 α t = 1 − β t \alpha_t = 1-\beta_{t} αt​=1−βt​ ， ϵ t − 1 ∼ N ( 0 , I ) \boldsymbol{\epsilon}_{t-1} \sim \mathcal{N}(0, \mathbf{I}) ϵt−1​∼N(0,I)

在前向过程中，有一个性质非常棒，就是我们其实可以通过 x 0 x_0 x0​ 和 β t \beta_{t} βt​ 直接得到 x t x_t xt​。

x t = α t x t − 1 + 1 − α t ϵ t − 1 = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 2 ) + 1 − α t ϵ t − 1 = α t [ α t − 1 ( α t − 2 x t − 3 + 1 − α t − 2 ϵ t − 3 ) + 1 − α t − 1 ϵ t − 2 ] + 1 − α t ϵ t − 1 = ⋯ = α t α t − 1 ⋯ α 1 x 0 + α t α t − 1 ⋯ α 2 1 − α 1 ϵ 0 + α t α t − 1 ⋯ α 3 1 − α 2 ϵ 1 + ⋯ + α t 1 − α t − 1 ϵ t − 2 + 1 − α t ϵ t − 1 \begin{array}{rlr} \mathbf{x}_{t} & =\sqrt{\alpha_{t}} \mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1} \\ \\ & = \sqrt{\alpha_{t}} \left( \sqrt{ \alpha_{t-1}}\mathbf{x}_{t-2} + \sqrt{1-\alpha_{t-1}}\boldsymbol{\epsilon}_{t-2} \right) + \sqrt{ 1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1}\\ \\ & = \sqrt{\alpha_{t}} \left[ \sqrt{ \alpha_{t-1}} \left( \sqrt{ \alpha_{t-2}}\mathbf{x}_{t-3} + \sqrt{1-\alpha_{t-2}}\boldsymbol{\epsilon}_{t-3} \right) + \sqrt{1-\alpha_{t-1}}\boldsymbol{\epsilon}_{t-2} \right] \\ \\ &+ \sqrt{ 1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1}\\ \\ &= \cdots\\ \\ &= \sqrt{\alpha_{t}} \sqrt{\alpha_{t-1}} \cdots \sqrt{\alpha_{1}} x_0 + \sqrt{\alpha_{t}} \sqrt{\alpha_{t-1}} \cdots \sqrt{\alpha_{2}}\sqrt{1-\alpha_{1}} \boldsymbol{\epsilon}_{0} \\ \\ &+ \sqrt{\alpha_{t}} \sqrt{\alpha_{t-1}} \cdots \sqrt{\alpha_{3}}\sqrt{1-\alpha_{2}} \boldsymbol{\epsilon}_{1} + \cdots + \sqrt{\alpha_{t}} \sqrt{1-\alpha_{t-1}} \boldsymbol{\epsilon}_{t-2} \\ \\ &+ \sqrt{1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1}\\ \end{array} xt​​=αt​ ​xt−1​+1−αt​ ​ϵt−1​=αt​ ​(αt−1​ ​xt−2​+1−αt−1​ ​ϵt−2​)+1−αt​ ​ϵt−1​=αt​ ​[αt−1​ ​(αt−2​ ​xt−3​+1−αt−2​ ​ϵt−3​)+1−αt−1​ ​ϵt−2​]+1−αt​ ​ϵt−1​=⋯=αt​ ​αt−1​ ​⋯α1​ ​x0​+αt​ ​αt−1​ ​⋯α2​ ​1−α1​ ​ϵ0​+αt​ ​αt−1​ ​⋯α3​ ​1−α2​ ​ϵ1​+⋯+αt​ ​1−αt−1​ ​ϵt−2​+1−αt​ ​ϵt−1​​ 其中， ϵ 0 ⋯ ϵ t − 1 \boldsymbol{\epsilon}_{0} \cdots \boldsymbol{\epsilon}_{t-1} ϵ0​⋯ϵt−1​ 都为标准正态分布，服从 N ( 0 , I ) \mathcal{N}(0, \mathbf{I}) N(0,I)。正态分布有两个性质：

所以上式中， α t α t − 1 ⋯ α 2 1 − α 1 ϵ 0 \sqrt{\alpha_{t}} \sqrt{\alpha_{t-1}} \cdots \sqrt{\alpha_{2}}\sqrt{1-\alpha_{1}} \boldsymbol{\epsilon}_{0} αt​ ​αt−1​ ​⋯α2​ ​1−α1​ ​ϵ0​服从正态分布，均值为0，方差为 α t α t − 1 ⋯ α 2 ( 1 − α 1 ) \alpha_{t} \alpha_{t-1} \cdots \alpha_{2} (1- \alpha_{1}) αt​αt−1​⋯α2​(1−α1​)，再由可加性，上式方差为： α t α t − 1 ⋯ α 1 + α t α t − 1 ⋯ α 2 ( 1 − α 1 ) + α t α t − 1 ⋯ α 3 ( 1 − α 2 ) + ⋯ ⋯ + α t ( 1 − α t − 1 ) + ( 1 − α t ) ϵ t − 1 = α t [ α t − 1 ⋯ α 2 ( 1 − α 1 ) + α t − 1 ⋯ α 3 ( 1 − α 2 ) + ⋯ ⋯ + ( 1 − α t − 1 ) − 1 ] + 1 = α t [ α t − 1 ⋯ α 2 ( 1 − α 1 ) + α t − 1 ⋯ α 3 ( 1 − α 2 ) + ⋯ ⋯ + α t − 1 ( 1 − α t − 2 ) − α t − 1 ] + 1 = α t α t − 1 [ α t − 2 ⋯ α 2 ( 1 − α 1 ) + α t − 2 ⋯ α 3 ( 1 − α 2 ) + ⋯ ⋯ + α t − 2 ( 1 − α t − 3 ) − α t − 2 ] + 1 = α t α t − 1 ⋯ α 3 [ α 2 ( 1 − α 1 ) + ( 1 − α 2 ) − 1 ] + 1 = 1 − α t α t − 1 ⋯ α 3 α 2 α 1 = 1 − α ˉ t \begin{array}{rlr} &\alpha_{t} \alpha_{t-1} \cdots \alpha_{1} + \alpha_{t} \alpha_{t-1} \cdots \alpha_{2} (1-\alpha_{1})+ \alpha_{t} \alpha_{t-1} \cdots \alpha_{3} (1-\alpha_{2}) + \cdots\cdots + \alpha_{t} (1-\alpha_{t-1}) \\ \\ &+ (1-\alpha_{t}) \boldsymbol{\epsilon}_{t-1} \\ \\ &= \alpha_{t} \left[\alpha_{t-1} \cdots \alpha_{2}(1-\alpha_1) + \alpha_{t-1} \cdots \alpha_{3}(1-\alpha_2) + \cdots\cdots + (1 - \alpha_{t-1}) - 1\right] + 1\\ \\ & = \alpha_{t} \left[\alpha_{t-1} \cdots \alpha_{2}(1-\alpha_1) + \alpha_{t-1} \cdots \alpha_{3}(1-\alpha_2) + \cdots\cdots+ \alpha_{t-1} (1-\alpha_{t-2}) - \alpha_{t-1} \right] + 1\\ \\ & = \alpha_{t}\alpha_{t-1} \left[\alpha_{t-2} \cdots \alpha_{2}(1-\alpha_1) + \alpha_{t-2} \cdots \alpha_{3}(1-\alpha_2) + \cdots\cdots+ \alpha_{t-2} (1-\alpha_{t-3}) - \alpha_{t-2} \right] + 1\\ \\ & = \alpha_{t}\alpha_{t-1} \cdots \alpha_{3} \left[ \alpha_{2} \left( 1 - \alpha_1 \right) + (1 - \alpha_2) - 1 \right] + 1\\ \\ &= 1- \alpha_{t}\alpha_{t-1} \cdots \alpha_{3}\alpha_{2}\alpha_{1} \\ \\ &= 1- \bar{\alpha}_{t} \end{array} ​αt​αt−1​⋯α1​+αt​αt−1​⋯α2​(1−α1​)+αt​αt−1​⋯α3​(1−α2​)+⋯⋯+αt​(1−αt−1​)+(1−αt​)ϵt−1​=αt​[αt−1​⋯α2​(1−α1​)+αt−1​⋯α3​(1−α2​)+⋯⋯+(1−αt−1​)−1]+1=αt​[αt−1​⋯α2​(1−α1​)+αt−1​⋯α3​(1−α2​)+⋯⋯+αt−1​(1−αt−2​)−αt−1​]+1=αt​αt−1​[αt−2​⋯α2​(1−α1​)+αt−2​⋯α3​(1−α2​)+⋯⋯+αt−2​(1−αt−3​)−αt−2​]+1=αt​αt−1​⋯α3​[α2​(1−α1​)+(1−α2​)−1]+1=1−αt​αt−1​⋯α3​α2​α1​=1−αˉt​​ 其中， α ˉ t = α t α t − 1 ⋯ α 3 α 2 α 1 \bar{\alpha}_{t} = \alpha_{t}\alpha_{t-1} \cdots \alpha_{3}\alpha_{2}\alpha_{1} αˉt​=αt​αt−1​⋯α3​α2​α1​，所以： x t = α t x t − 1 + 1 − α t ϵ t − 1 = α ˉ t x 0 + 1 − α ˉ t ϵ \begin{array}{rlr} \mathbf{x}_{t} & =\sqrt{\alpha_{t}} \mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1} \\ \\ & = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon} \end{array} xt​​=αt​ ​xt−1​+1−αt​ ​ϵt−1​=αˉt​ ​x0​+1−αˉt​ ​ϵ​

因此任意时刻的 x t x_t xt​ 满足： q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right) q(xt​∣x0​)=N(xt​;αˉt​ ​x0​,(1−αˉt​)I)

之所以要令 α t = 1 − β t \alpha_t = 1-\beta_{t} αt​=1−βt​，是因为只有这样才能推导出2.1.2中的结果。在原论文中， T T T 设为1000，即要进行1000次扩散加噪过程，每次扩散过程的参数关系为： β 1 < β 2 < … < β T \beta_{1}