本篇将举三个重要的理论或领域，以展示之前信号理论的应用和意义。其中滤波理论和通信系统是非常大的应用领域，这里仅对基础的概念和方法做个介绍，以作入门之用。

　　在系统函数的性质中，我们看到信号在时域上的微分、积分、卷积等复杂运算，在频域都变成了代数运算。这说明分析和使用信号的频域，有其天然的优势，也会带来更广泛的应用。当然，频域的操作最终都体现在时域上，注意讨论其相互关系和平衡，有时也是必需的。滤波系统主要就是以信号的频域为操作对象，具体来说就是调整不同基波的波幅、相位，以使输出信号满足具体需求，这样的系统也叫滤波器（Filter）。

　　在讨论具体滤波器之前，有必要先说清楚系统对信号的频域究竟产生了什么影响。信号的频谱系数\(X(j\omega)\)是一个复值函数，模\(|X(j\omega)|\)表示基波峰谷的高度，它称为频谱的幅度；角度\(\sphericalangle X(j\omega)\)表示基波初始位置，它称为频谱的相位。LIT系统就是将信号的频谱乘上了系统函数\(H(j\omega)\)，把影响按幅度和相位分开讲，\(|H(j\omega)|\)称为系统的增益（gain），\(\sphericalangle H(j\omega)\)叫系统的相移（phase shift）。

　　将频谱的幅度、相位分开展示的坐标图（横坐标为\(\omega\)）叫模-相图，根据对称性，它们仅需显示正频率部分。为了展示更多的基波频率，以及在系统中经常出现\(\log_{10}\omega\)，横坐是对数尺度的。另外，从图中表示相移对相位的影响是简单的，只需在相位上增加相移即可。为了让增益的影响也同样直观，一般把幅度坐标用对数表示，改乘法为加法。其实在现实中，人们对幅度的感知也是对数形式的，比如音量和功率\(\log_{10}|X|^2\)成正比。一般把\(\log_{10}|X|^2\)的单位叫做Bel，更常用的单位分贝（dB）是其十分之一，也即模坐标的值是\(20\log_{10}|X(j\omega)|\)。使用以上所有方法的图示称为Bode图。

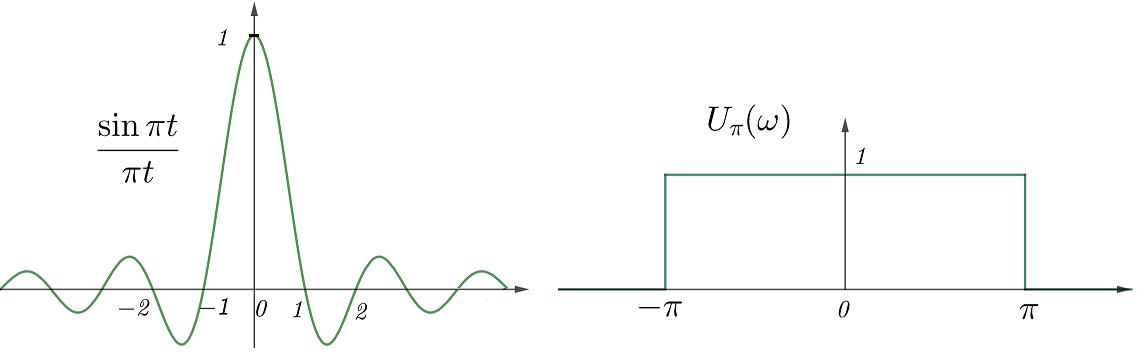
　　滤波器一般通过修改幅度的方法，选择性保留部分频率的基波、而削弱其它频率的基波，增益恒为\(1\)的叫全通系统。根据保留频率的不同，有很多直观的术语，这里就不一一阐述了，比如低通/高通/带通滤波、以及滤波的截止频率/通带/阻带。另外，系统的相移会造成基波的时移，这在关心时移的场景里（比如图片），同样是不可忽略的影响。所有不期望发生的增益和相移，都被称为信号的失真。根据信号时移的性质，相同的时移\(t_0\)对应相移\(\omega t_0\)，相移要和频率成正比信号才不失真，\(t_0\)称为系统的群时延。在一般系统的局部，也有近似的群时延\(\tau(\omega)\)（式（1））。

\[\sphericalangle H(j\omega)=\omega\cdot\tau(\omega)+\phi(\omega),\;\;\tau(\omega)=\dfrac{\text{d}[\sphericalangle H(j\omega)]}{\text{d}\,\omega}\tag{1}\]

　　理想的滤波器的系统函数只有\(0\)和\(1\)两种值，这里就举例不同场景的低通滤波，高通/带通滤波可由其转变而来。为方便叙述，先定义方波函数\(U_T(x)\)，它仅在\(|x|\leqslant T\)时取\(1\)。如果设低通滤波器\(X(j\omega)\)为\(U_W(\omega)\)，不难得到其单位冲激响应\(x(t)\)（式（2）左）。你可以记忆\(\text{sinc}\,\pi t\overset{F}{\leftrightarrow}U_{\pi}(\omega)\)，另外在\(t=0\)处就取周边极限值。利用对偶性，就可以得到方波冲激响应的系统函数（式（2）右）。

\[\dfrac{\sin Wt}{\pi t}\;\overset{F}{\leftrightarrow}\;U_W(\omega);\;\;U_T(t)\;\overset{F}{\leftrightarrow}\;\dfrac{2\sin T\omega}{\omega}\tag{2}\]

　　如果记\(\text{sinc}(t)=\sin t/t\)，则式（2）左就是\(W\text{sinc}(Wt)/\pi\)。对于比较大的\(W\)，它就是\(\text{sinc}(t)\)的横向压缩以及纵向拉升，且能量都集中在原点附近。当\(W\to\infty\)时，可知左式在\(t=0\)处趋于无穷，利用三角积分的值还能算得原点附近的积分趋于\(1\)。这非常类似\(\delta(t)\)，其实\(W\to\infty\)时\(U_W(\omega)\)是全通滤波，故它的单位冲激响应就是\(\delta(t)\)（即恒等变换）。同样道理，式（2）右中\(T\to\infty\)时的系统函数近似\(2\pi\delta(\omega)\)，这与周期函数的FT相一致。

　　为讨论离散信号，对于周期\(T\)，先定义周期方波\(U_{\theta}(x)\)，它仅在\(|x-kT|\leqslant \theta T/2\)时为\(1\)。对离散信号的FT，设低通滤波器\(X(j\omega)\)为\(U_{\theta}(\omega)\)，不难得到其单位脉冲响应\(x(t)\)（式（3）左），其中\(a_0=\theta\)。滤波\(U_{\theta}(\omega)/(2\theta\pi)\)每个周期的积分恒为\(1\)，当\(\theta\to 0\)时即为单位冲激串，左边恒有极限\(1/(2\pi)\)，与定值的FT一致。然后利用对偶性，也能得到周期方波的FS（式（3）右），以及单位冲激串的FS恒为\(1/T\)。最后还有离散方波的FT，以及周期离散方波的FS（式（4）），这里暂不考虑FS上的滤波。

\[\dfrac{\sin(n\theta\pi)}{n\pi}\;\overset{F}{\leftrightarrow}\;U_{\theta}(\omega);\;\;U_{\theta}(t)\;\overset{FS}{\leftrightarrow}\;\dfrac{\sin(k\theta\pi)}{k\pi}\tag{3}\]

\[U_{n_0}(n)\;\overset{F}{\leftrightarrow}\;\dfrac{\sin[\omega(n_0+1/2)]}{\sin(\omega/2)};\;\;U_{\theta}[n]\;\overset{FS}{\leftrightarrow}\;\dfrac{\sin(k\theta\pi)}{N\sin(k\pi/N)}\tag{4}\]

　　一个滤波器不光要考虑频域的效果，还要顾及时域带来的特性，一般用单位阶跃响应考察滤波器的时域特征。它逐步收敛于单位冲激响应的极限值，收敛过程中，有几个参数比较影响系统的好坏。首先上升到稳态的时间，表示系统响应的快慢（或当前信号对后续输出的影响大小），一般越快越好。然后还有进入稳态前的超量（超出稳定值）、以及进入稳态时的震荡，它们都影响了系统的稳定速度，可能降低系统实时性。

　　式（2）左的理想滤波不光有超量和震荡，现实中还很难实现（不是有理系统），另外还需要整个输入信号才行（非因果系统），实际上很少使用。非理想滤波在通带和阻带之间没有明显的界限，而是有一定长度的过渡带，并且通带/阻带上都可能有一些起伏，以此可以换来时域更好的特性。一般越小的过渡带、越小的起伏，会带来更大的超量和震荡、以及更长的上升时间，使用中需要注意平衡。更多具体的滤波要到后续课程中讨论了。

　　离散时间信号更方便处理，经常要把连续信号\(x(t)\)采样成离散序列\(x[nT]\)，为此需要从理论上分析这两种信号的关系。首先自然地想把采样表示成\(x(t)s(t)\)，其中\(s(t)\)仅在\(t=nT\)处有非零值\(1\)，但由于\(s(t)\)没有正常的分析性质（微积分），频域分析无法进行。为此可以把\(s(t)\)换成单位冲激串函数\(p(t)\)（式（5）左），上一节已经知道它的FS频谱是\(1/T\)，故它的FT频谱系数是式（5）右（\(\omega_s=2\pi/T\)）。

\[p(t)=\sum_{k\in\Bbb{Z}}\delta(t-kT)\;\overset{F}{\leftrightarrow}\;P(j\omega)=\omega_s\sum_{k\in\Bbb{Z}}\delta(\omega-k\omega_s)\tag{5}\]

　　记采样信号为\(x_p(t)=x(t)p(t)\)，根据乘法性质知其频谱系数为\(X_p(j\omega)=\dfrac{1}{2\pi}X(j\omega)*P(j\omega)\)。式（5）带入便知，\(X_p(j\omega)\)是多个\(X(j\omega)*\delta(\omega-k\omega_s)/T\)的累加，而后者是\(X(j\omega)/T\)平移\(k\omega_s\)得到，故\(X_p(\omega)\)就是\(X(j\omega)/T\)以\(\omega_s\)为周期的叠加。如果\(x(t)\)的带宽满足\(\omega_c\omega_s\)时，信号恢复会出现不可预知的结果，比如对信号\(\cos\omega_0 t\)低速度采样时，恢复信号的频率总会下降到\(|\omega_s-k\omega_0|\)（自行证明），这个可以解释视频中风扇倒转的现象。

　　现在就来讨论从采样函数\(x_p(t)\)恢复出\(x(t)\)的一般性方法，这里\(x_p(t)\)是个数学工具，它代表了采样信息\(x[nT]\)。记恢复系统的单位冲激响应为\(h(t)\)，则恢复信号\(x_r(t)\)为式（6）。不难看出，满足\(h(0)=1,h(nT)=0,(n\ne 0)\)的系统都能准确恢复出采样值\(x[nT]\)，这时的\(x_r(t)\)就好像\(x[nT]\)的内插函数。采样定理中的低通方波就满足插值条件，其它恢复信号的插值法也要满足插值条件，而且在频谱上都是低通方波的一种近似，即便只是粗略的近似。

\[x_r(t)=x_p(t)*h(t)=\sum_{n\in\Bbb{Z}}x(nT)h(t-nT)\tag{6}\]

　　把式（6）看成\(x(nT)\)影响的叠加，选择适当的\(h(t)\)便可以构造不同的恢复系统。比如记\(h_0(t)\)仅在\([0,T)\)上有非零值\(1\)，这时\(x_r(t)\)在\([nT,(n+1)T)\)上的值都是\(x(nT)\)，这样的阶梯函数叫采样的零阶保持。为了让恢复信号连续，最简单的就是线性插值（相邻两点直线相连，也叫一阶保持），不难得知\(h(t)\)是一个\((-T,T)\)上面的三角形函数。类似地可以有更平滑的高阶保持，那里\(h(t)\)要更平滑，每个点的影响范围也更大。

　　连续信号（也叫模拟信号（analog））离散化的优点并不仅限于存储和传输，数字（digital）信号的在处理上有更多有效便捷的方法。所以经常会把模拟信号先做个模-数转换（A/D），通过数字信号处理（DSP）后，再进行数-模转换（D/A）输出模拟信号。在这个过程中，要想使用统一的FT理论就非常困难了，而不得不直接寻找连续FT和离散FT之间的关系，也即冲激采样\(x_p(t)\)能否由脉冲采样\(x_d[n]=x[nT]\)替代。

　　把\(x_p(t)\)看成冲激串的叠加，并根据\(\delta(t-nT)\)的（连续FT）频谱，可得到\(x_p(t)\)的频谱为式（7）左。然后直接用离散FT的公式，可得到\(x_d[n]\)的频谱为式（7）右，这里的\(X_d(e^{j\omega})\)已经展开为周期函数。这两个频谱系数虽然来自不同的变换，但却有式（8）左的联系，\(X_d(e^{j\omega})\)是\(X_p(j\omega)\)在横轴拉升\(T\)倍，使周期成为\(2\pi\)。这个结论不仅说明了\(x_p(t)\)和\(x_d[n]\)在信息量上的等价性，还是连续频谱和离散频谱之间的桥梁。

\[X_p(j\omega)=\sum_{n\in\Bbb{Z}}x(nT)e^{-j\omega nT};\;\;X_d(j\omega)=\sum_{n\in\Bbb{Z}}x(nT)e^{-j\omega n}\tag{7}\]

\[X_p(j\omega/T)=X_d(e^{j\omega});\;\;H(j\omega)=H_d(e^{j\omega T}),\,(|\omega|