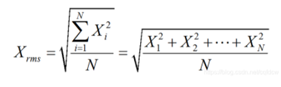深入浅出数据分析 |
您所在的位置:网站首页 › 深入浅出的分析 › 深入浅出数据分析 |
深入浅出数据分析
|
11 误差
11.1 插值法
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。 插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。 11.1.1 定义给定 n个离散数据点(称为节点) f(x)为定义在区间 [a,b]上的函数。 则称g(x)为f(x)关于节点 插值法的中心议题是:在我们己具备一组表列数(tabulated value)的情况下,如何得出没被定义在区域的值。 我们会要用到插值法的场合往往都不知道描述对象背后的函数是什么形式(但相信其有连续的本质),因此我们也只能尽力求真实。 使用插值法所建立的函数,在表列点上一定要重现原本给定的表列值,否则就不是插值法而是函数近似或曲线拟合的问题了,它们是不一样的。 插值的作法,很直观地来讲,就是,(1) 先从表列值来获得函数f(x),再 (2) 用函数 f(x) 求出我们所要的任何特定x 之 f(x) 函数值。然而, 比较精密且系统化的数值方法却不是用这两个步骤来进行插值, 原因是前述两阶段方法对於插值的精密度并没有控制,效率较差, 也比较会有进位误差。一般在做插值法,是从欲插值点x 附近的几个表列点xi 开始,建立插值函数 f(x),并且也试着网罗更多表列点来插值,看随着项数变多误差会不会变小,如此找出最适合的函数f(x)。 我们会比较希望演算法在从表列值建立插值用函数时,也能提供误差分析以供我们或程式来判断。毕竟可用的插值函数f(x) 并非唯一,而即便是己设定了采用一种方法,如多项式法,也会有该使用多少项才最恰当的问题。 建立插值函数所需之邻近表列值个数,我们称之为插值法的 order (阶) ,较高阶未必保证得到较合理的插值,这点在多项式插值法尤其如此,要小心注意。详见课文中之例图
两图实线都是原现象背後的真正值,短虚线代表低阶多项式插值结果,长虚线代表高阶多项式插值结果。明显可见,case (a) 高阶者较准确,而case (b) 则是低阶较准确。 11.1.3 外插法用回归方程预测数据范围以外的数值称为外插法。 外插法与内插法不同,内插法对数据范围内的点进行预测,这正是回归法的本来目的。内插法很准确。如果需要使用外插法,需要指定附加假设条件,明确表示不考虑数据集外发生的情况。 11.1.4 线性插值法(Linear Interpolation)所有的插值法里面最简单的莫过於线性插值法,任两个相邻的表列点之间必可以拉一条直线把它们连起来,如此在之间的x 值就都有线性函数y(x) 可以对应到,利用直线上的斜率必为固定值的特性,其公式是(以(x1,y1)、 (x2,y2) 为两个相邻的表列点为例) : (y - y1) / (x - x1) = (y2 - y1) / (x2 -x1) 经整理後得 y = [ (y2 -y1) / (x2 - x1) ] (x - x1) + y1注意等号的右边全是x 与常数,我们因此有了y(x) 的明确公式可用。 我要求大家对於线性插值法这种较简单的插值法,应该要能在不看参考资料的情况下做出,即自行把式子写下来,并且把程式写出来。 11.1.5 多项式插值法大家都知道两点唯一决定一条直线(不转弯)、三点唯一决定一条二次曲线(会转一次弯)、四点唯一决定一条三次曲线(会转两次弯,有反曲点),等等。这些曲线都是以多项式的形式(变数出现时,些是整数次方) 。 一个 n - 1 次曲线的多项式虽有像y = a(n-1)x(n-1) + a(n-2)x(n-2) + .... + a1x +a0这样的通式可以表示出, 但必须代入n 个表列值才能定出 an-1 至 a0 那 n 个系数, 一下子不易看出。 数学上有一个Lagrange 多项式公式,它可以由n 对 (x,y) 值唯一决定 n-1 阶多项式,且公式非常好记,如课文中的式(3.1.1)
1.回归一般指线性回归,是求最小二乘解的过程。反映的是两组数据之间的关系。 2.多项式插值:用一个多项式来近似代替数据列表函数,并要求多项式通过列表函数中给定的数据点。(插值曲线要经过型值点。) 3.多项式逼近:为复杂函数寻找近似替代多项式函数,其误差在某种度量意义下最小。(逼近只要求曲线接近型值点,符合型值点趋势。) 4.多项式拟合:在插值问题中考虑给定数据点的误差,只要求在用多项式近似代替列表函数时,其误差在某种度量意义下最小。 注意: 表列函数:给定n+1个不同的数据点( 逼近函数:求一函数,使得按某一标准,这一函数y=f(x)能最好地反映这一组数据即逼近这一表列函数,这一函数y=f(x)称为逼近函数 插值函数:根据不同的标准,可以给出各种各样的函数,如使要求的函数y=f(x)在以上的n+1个数据点出的函数值与相应数据点的纵坐标相等,即 插值和拟合都是函数逼近或者数值逼近的重要组成部分。 他们的共同点都是通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律的目的,即通过“窥几斑”来达到“知全豹”。 简单的讲,所谓拟合是指书籍某函数的若干离散函数值{f1,f2,…,fn},通过调整该波函数中若干选定系数ƒ (λ1, λ2,…, λ3),使该函数与书籍点集的差别(最小二乘意义)最小。如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫做作非线性拟合或者非线性回归。各地怕啊也可以是分段函数,这种情况下叫作样条拟合。 而插值是指已知某函数的在若干离散点上的函数值或者导数信息,通过求解该函数中待定形式的插值函数以及待定系数,使得该函数在给 定离散点上满足约束。插值函数又叫作基函数,如果该基函数定义在整个定义域上,叫作全域基,否则叫作分域基。如果约束条件中只有函数值的约束,叫作Lagrange插值,否则叫作Hermite插值。 从几何意义上将,拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。 11.2 机会误差(残差) 11.2.1 定义残差在数理统计中是指实际观察值与估计值(拟合值)之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话, 我们可以将残差看作误差的观测值。 它应符合模型的假设条件,且具有误差的一些性质。利用残差所提供的信息,来考察模型假设的合理性及数据的可靠性称为残差分析。 11.2.2 特征在回归分析中,测定值与按回归方程预测的值之差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。δ*遵从标准正态分布N(0,1)。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合。 显然,有多少对数据,就有多少个残差。残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。 11.2.3 分析为了更深入地研究某一自变量与因变量的关系,人们还引进了偏残差。此外, 还有学生化残差、预测残差等。以某种残差为纵坐标,其它变量为横坐标作散点图,即残差图 ,它是残差分析的重要方法之一。通常横坐标的选择有三种: (1) 因变量的拟合值; (2)自变量; (3)当因变量的观测值为一时间序列时,横坐标可取观测时间或观测序号。 残差图的分布趋势可以帮助判明所拟合的线性模型是否满足有关假设。如残差是否近似正态分布、是否方差齐次,变量间是否有其它非线性关系及是否还有重要自变量未进入模型等。.当判明有某种假设条件欠缺时, 进一步的问题就是加以校正或补救。需分析具体情况,探索合适的校正方案,如非线性处理,引入新自变量,或考察误差是否有自相关性。 11.2.4 方差、协方差、标准差、均方差、均方根值、均方误差、均方根误差标准偏差让所有人是平均值周围的分布情况。 均方根误差描述的是回归线周围的分布情况。 11.2.4.1 方差(Variance) 方差用于衡量随机变量或一组数据的离散程度,方差在在统计描述和概率分布中有不同的定义和计算公式。①概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度;②统计中的方差(样本方差)是每个样本值与全体样本均值之差的平方值的平均数,代表每个变量与总体均值间的离散程度。 概率论中计算公式 离散型随机变量的数学期望:
连续型随机变量的数学期望: 其中,pi是变量,xi发生的概率,f(x)是概率密度。
统计学中计算公式 总体方差,也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差:
其中,n表示这组数据个数,x1、x2、x 3……xn表示这组数据具体数值。
其中, 样本方差,无偏方差,在实际情况中,总体均值
此处,为什么要将分母由n变成n-1,主要是为了实现无偏估计减小误差。 11.2.4.2 协方差(Covariance) 协方差在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
其中,E[X]与E[Y]分别为两个实数随机变量X与Y的数学期望,Cov(X,Y)为X,Y的协方差。 11.2.4.3 标准差(Standard Deviation) 标准差也被称为标准偏差,在中文环境中又常称均方差,是数据偏离均值的平方和平均后的方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度,只是由于方差出现了平方项造成量纲的倍数变化,无法直观反映出偏离程度,于是出现了标准差,标准偏差越小,这些值偏离平均值就越少,反之亦然。
其中, 代表所采用的样本X1,X2,...,Xn的均值。
其中, 代表总体X的均值。 例:有一组数字分别是200、50、100、200,求它们的样本标准偏差。 = (200+50+100+200)/4 = 550/4 = 137.5 = [(200-137.5)^2+(50-137.5)^2+(100-137.5)^2+(200-137.5)^2]/(4-1) 样本标准偏差 S = Sqrt(S^2)=75 11.2.4.4 均方误差(mean-square error, MSE) 均方误差是反映估计量与被估计量之间差异程度的一种度量,换句话说,参数估计值与参数真值之差的平方的期望值。MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
11.2.4.5 均方根误差(root mean squared error,RMSE) 均方根误差亦称标准误差,是均方误差的算术平方根。换句话说,是观测值与真值(或模拟值)偏差(而不是观测值与其平均值之间的偏差)的平方与观测次数n比值的平方根,在实际测量中,观测次数n总是有限的,真值只能用最可信赖(最佳)值来代替。标准误差对一组测量中的特大或特小误差反映非常敏感,所以,标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。因此,标准差是用来衡量一组数自身的离散程度,而均方根误差是用来衡量观测值同真值之间的偏差。
11.2.4.6 均方根值(root-mean-square,RMES) 均方根值也称作为方均根值或有效值,在数据统计分析中,将所有值平方求和,求其均值,再开平方,就得到均方根值。在物理学中,我们常用均方根值来分析噪声。
比如幅度为100V而占空比为0.5的方波信号,如果按平均值计算,它的电压只有50V,而按均方根值计算则有70.71V。这是为什么呢?举一个例子,有一组100伏的电池组,每次供电10分钟之后停10分钟,也就是说占空比为一半。如果这组电池带动的是10Ω电阻,供电的10分钟产生10A 的电流和1000W的功率,停电时电流和功率为零。 |
【本文地址】
今日新闻 |
推荐新闻 |



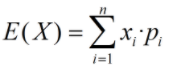 ---------求取期望值
---------求取期望值 ----------求取期望值
----------求取期望值 -----------求取总体均值
-----------求取总体均值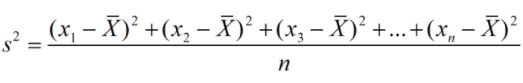 -----------求取总体方差
-----------求取总体方差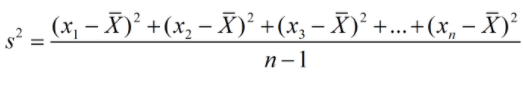 --------------求取样本方差
--------------求取样本方差 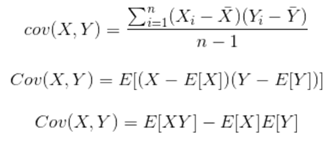
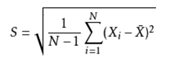 ------------求取样本标准差
------------求取样本标准差 -------------求取总体标准差
-------------求取总体标准差