小镇做题家当然是来做题的（x）

其实最开始是因为朋友找我补补考研数学，在讲课的过程中重新捋了一遍这部分的内容记了下来。后面逛群里逛B站的时候，发现似乎要么是卖课（当然我没买过），要么都是东一块西一块扯方法技巧，不成体系。所以突然就想写一篇《泰勒展开观点下的极限题》，然后想着想着就扩充出了这篇文章（

那就氵一下吧，从最初的开始说起。

泰勒展开是微积分里最伟大的数学发现之一。后续发展出的和其他方面更深的联系先不说，本篇只是入门。所以最浅显直接的，泰勒展开展现出两种意义：

1、将任意的解析函数多项式化。

2、它表明了解析函数在任意点上的取值实际上都只受某一指定点的控制。

首先看第一点：多项式化。

初等函数中，三角函数 \sin x ， \cos x ；指数函数 \mathrm e^ x ；对数函数 \ln x ；反三角函数 \arcsin x 等，它们的值除了一些特殊点外，其他值都是难以计算的。不止是难以计算，实际上它们的计算过程都是难以想象的。如 \sin (3) ，这个值应该怎么算呢？

想不到吧？初等函数都尚且无法做到，就更不用说更多奇形怪状的函数了。

实际上我们真正能够想象和操作的运算只有四则运算：加减乘除，再多上一个乘方。开方都是比较困难的行为。而这些的处理对象都是幂函数，或者说是整数次幂的幂函数。因此泰勒展开对于在第一点的目的就可以理解了：将奇形怪状、难以求值的函数多项式化。

而如何多项式化呢？

如，现在令待多项式化的函数为 f(x)=\sin x ，假定多项式化后的结果为 P(x)=a_0+a_1x+a_2x^2+\cdots

现在 f(x)=\sin x 是已知且不好算的函数，而 P(x)=a_0+a_1x+a_2x^2+\cdots 的各项的系数 \{a_0,a_1,a_2,\dots\} 还是尚未确定的，因此这个是未知但好算的函数。现在就来求这些系数到底是什么。

既然叫做多项式化，那么这个“多项式化”的前后二者必然是相等的。二者相等，要如何相等来求这些系数的值呢？

最简单的想法当然是每个点都相等：

\sin(0)=P(0),\sin(1)=P(1),\sin(\sqrt2)=P(\sqrt2),\sin(x_1)=P(x_1)\dots\\这样的相等是最简单的，但是没有意义啊。因为左边 \sin(?) 的值不就是难求的吗？就是求不出来才要多项式化嘛。

另一种想法就更为巧妙一点。既然 \sin x 还是有一些特殊的点能求出来的，那就在这些点上做文章。比如在 x=0 这个点。首先二者相等，那肯定值得相等： \sin(0)=P(0) 。 \sin x 在这个点的导数也是能具体求出数值的，那么再让导数相等： \sin'(0)=P'(0) 。由此推广到任意阶导数都相等，那么不就是找到了另一种相等的方式了吗？即：

f(x)\equiv P(x)\ \Rightarrow\ \begin{cases}f(0)=P(0)\\f'(0)=P'(0)\\f''(0)=P''(0)\\\dots\end{cases}\\ 这样一来，左边是好算的已知量；右边是待求的位置系数 a_i ：

\begin{align}f(0)&=\sin(0)=0\qquad &P(0)&=a_0+a_1\cdot 0+a_2\cdot0^2+\dots&=0!a_0\\f'(0)&=\cos (0)=1\qquad &P'(0)&=a_1+2a_2\cdot0+3a_3\cdot0^2+\dots&=1!a_1\\f''(0)&=-\sin (0)=0\qquad &P''(0)&=2a_2+3\cdot2a_3\cdot0+4\cdot3a_4\cdot0^2+\dots&=2!a_2\\f'''(0)&=-\cos (0)=-1\qquad &P'''(0)&=3\cdot2a_2+4\cdot3\cdot2a_3\cdot0+\dots&=3!a_3\\&\dots&&\dots\end{align}\\ 左右两边分别相等： f^{(i)}(0)=P^{(i)}(0) ，那么对应就有：

\begin{align}0&=0!a_0\qquad &a_0&=0\\1&=1!a_1\qquad &a_1&=1\\0&=2!a_2\ \qquad &a_2&=0\\-1&=3!a_3&a_3&=-\frac1{3!}\\0&=4!a_4\qquad&a_4&=0\\&\dots&&\dots\end{align}\\ 故而：

\begin{align}f(x)&=P(x)\\\sin x&=0+x+0-\frac1{3!}x^3+0+\dots\end{align}\\ 这样便得到了 \sin x 函数的多项式化的表达，这样的过程即泰勒展开。

如果对于任意的 f(x) ，如前面举例的初等函数 \mathrm e^x,\cos x 等，我们知道它们在 x=0 处的各阶导数的值都是容易求出的，那么也就可以通过同样的方式展开。进一步的说，哪怕某一个 f(x) 是我们闻所未闻见所未见也不是通过初等函数组合起来的，在 x=0 处各阶导数我们不知道呢？那同样也可以这样展开。前面一直说“在 x=0 处的值可以求出来”这种话，看上去似乎必须得能求才能在这个点展开，但是实际上这种展开的方法显然是不依赖于到底能不能求的。哪怕不能求出来，也同样可以写出这样的表达：

通过上面式子的对比，显然可以看出来对于展开的第 i 项有： f^{(i)}(0)=P^{(i)}(0)=i!a_i\quad\Rightarrow\quad a_i=\frac{f^{(i)}(0)}{i!}\\ 于是：

\begin{align}P(x)&=a_0+a_1x+a_2x^2+\dots\\&=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\dots+\frac{f^{(i)}(0)}{i!}x^i+\dots\end{align}\\由于 P(x) 是 f(x) 的多项式化，二者是恒等的， f(x)\equiv P(x) ，那么就不再单独标记出一个 P(x) 出来，上面的式子直接左边用 f(x)= 接上去，那么就有：

f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\dots+\frac{f^{(i)}(0)}{i!}x^i+\dots\\ 或者放在求和号里面：

f(x)=f(0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(0)}{i!}x^i}\\这样的式子当然是标准且成立的，展开的函数 f(x) 不限于初等函数，而是任何解析函数均可。虽然均可，但是右边展开的各项若要真正写出来的话那还是必须得带入 f^{(i)}(0) ​进去，那么如果 f(x) 真是任意奇形怪状的函数，这些个值都是不知道的话，虽然式子成立，但是里面全是一大堆不知道的东西，那似乎这个展开就没什么意义了…

…吗？

这个问题在后面物理的部分再谈。届时会发现，哪怕不知道 f^{(i)}(0) 的值，只是对假想函数的抽象展开，那也是十分有意义的。

但是现在在这个阶段的微积分里，各类初等函数在 x=0 ​处的展开是最有价值的，因为它们各阶导数的值在此都能轻松的求得。

注意观察泰勒展开的公式，可以发现在公式的左右两侧都出现了函数“ f ”。但左边的是作用在变量 x 下的 f ： f(x) ；而右边的 f 则只是作用在 0 处的值： f(0) 和 f^{(i)}(0) ——而变量 x ，则是出现在幂函数 x^i 里。这说明什么？当 f(x) 里的 x 变化时，它只能控制幂函数 x^i 里的 x 变化，而 f(0) 和 f^{(i)}(0) 它是控制不了的，这个取值虽然和 f 有关，但它早已被 x=0 ​这个点固定。

如若我们来实现最开始提出的设想：求出 \sin (3) 。将 \sin x 展开后，带入自变量 x=3 ，则可以轻松写出来：

\sin (3)=\sin (0)+\frac{\sin' (0)}{1!}\cdot3+\frac{\sin'’ (0)}{2!}\cdot3^2+\frac{\sin''' (0)}{3!}\cdot3^3+\dots\\再次对应一下上面的说法：注意看右边，自变量是出现在幂函数里，幂次是容易求的；各阶导数的取值是固定在 x=0 处，这个值是易求的。因此通过泰勒展开则把 \sin(3) 这一无法想象的求值变成了四则运算的简单求值（虽然得是无限项…）。

再次注意看两边的 \sin 函数，左边的 \sin() 里面当然不止是能填 3 ，任意数都可以。而右边的 \sin 确是固定 x=0 处取值的。任意 f(x) 的展开表达也是如此，可以认为， f 在任意 x ​下的值实际上都由一个点的取值“控制”了。

这就是第二条：解析函数在任意点上的取值实际上都只受某一指定点的控制。

这非常神奇，任意处的取值居然能由一个点来决定？似乎这个函数所有的信息都蕴藏在了一个点里一样。或者说，似乎你只要随便写一系列的 \{f^{(i)}(0)\} ​出来，放进泰勒展开里去，那它就自然而然的生成了一个函数。

就是这么神奇。实际上，有这么神奇性质的函数才叫做解析函数（循环论证了x）

再写一遍：

f(x)=f(0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(0)}{i!}x^i}\\泰勒展开的记忆可以分为四部分：

1、 f(0) 先列出来。在 x=0 处展开肯定得是从 f(0) 处开始嘛。在这个点右边求和的幂函数全都变成零了，所以就是 f(0)=f(0) ，这是显然的。

右边的求和分为三部分：

2、分子 i 阶导： f^{(i)}(0) 。注意，取值是在展开点取值的。

3、分母 i 阶乘： i! 。

4、右边 i 次方： x^i ​​。这里才是容纳自变量的地方。自变量都变成幂函数了。

所以看泰勒展开就看四个部分就行了，而一般来说， f(0) 画个图总能记住的，总不能图像长啥样都不知道吧？所以只需要记求和的三部分就行。而求和的分母和右边都是固定的，所以真正要记忆的只有分子是什么。因此其实也就没什么难记的了。

实际上这样在 x=0 处的泰勒展开有一个专门的名字：麦克劳林展开。后面如果需要特别体现展开点的话，就都换成这个称呼了。

上面的是抽象的麦克劳林展开，而在高数中要用的当然是具体函数的麦克劳林展开。

下面写一些常见的（考研肯定要学的）展开。

指数函数：

\mathrm e^x=1+x+\frac1{2!}x^2+\frac1{3!}x^3+\dots\\指数函数展开的记忆点就是：分子都是1。

多项式展开：

(1+x)^n=1+nx+\frac{n(n-1)}{2!}x^2+\frac{n(n-1)(n-2)}{3!}x^3+\dots\\多项式展开的记忆点就是：从 n 往下减1，多一次幂，就减一个1，乘上去。

常用的有：

\begin{align}\sqrt{1+x}&=(1+x)^{\frac12}=1+\frac12x+\dots\\\frac1{\sqrt{1+x}}&=(1+x)^{-\frac12}=1-\frac12x+\dots\\\frac1{1+x}&=(1+x)^{-1}=1-x+\dots\end{align}\\只写两项是因为前两项尤其好记忆，可以通过这种方式给读者加深印象：就是把指数放到前面来变成系数就行了。但是，前两个请读者务必再往后写一项，这是易错的地方，不限于：减一减错、漏分母、符号错误、算错。而最后一个则是为了提醒：看着是分母的东西，其实也可以通过这个展开变成相乘，所以分母在某些时候可以变成“不是分母”。

当然，第三个的展开就不要傻乎乎的套多项式展开的式子了，这是个几何级数！ \frac1{1+x}=\frac1{1-(-x)} ，是首项是 1 ，公比是 (-x) 的几何级数：

1+(-x)+(-x)^2+(-x)^3+\dots=\frac1{1+x}\\ 另外， (1+x)^{\frac1x} 这种东西不能用多项式展开！

三角函数：

\begin{align}\sin x&=x-\frac16x^3+\frac1{5!}x^5+\dots\\\cos x&=1-\frac12x^2+\frac1{4!}x^4+\dots\end{align}\\ 如何记忆这两个函数的展开呢？

首先要注意到，无论是 \cos 还是 \sin 的导数都是 0,1,0,-1,\dots 的循环：“ 0 ”意味着某些项的缺失，而 \pm 1 则是意味着符号的交替。当然，还有分母的阶乘和右边的幂次，这些都是不用记忆的东西，而正负交替，显然，都是从正的开始的，下一个负的，正负正负的来。那么现在主要看的就是：要哪些项？

这里只需要注意到一个东西， \sin x 是奇函数， \cos x 是偶函数。奇函数当然展开后应当只有奇数的幂次，偶函数展开后当然只有偶数的幂次。所以 \sin x 的展开当然是 ?x^1+?x^3+\dots 的形式，而 \cos x 的展开当然是 ?x^0+?x^2+\dots 的形式。这就确定了它们所能拥有的幂次。

所以如若要写出 \sin x 的展开，则先回想起来这是个奇函数，写出奇数次的幂函数，然后正负正负的补上正负号，再补上分母的阶乘，就得到了展开式。读者自行尝试，并写出 \cos x ​的展开。

除此之外再需要单独记忆一个 \tan x 的展开。

对于正切，要想严格得到任意项的展开表达有些困难了，但最重要的是：没有必要记任意项的（√）。实际上由 \tan x=\frac{\sin x}{\cos x} 的定义再加上上面这俩的展开可以直接简单的展开两项出来，记两项就够了。

\begin{align}\tan x=\frac{\sin x}{\cos x}=\frac{x-\frac16x^3+\dots}{1-\frac12x^2+\dots}&=(x-\frac16x^3+\dots)(1-\frac12x^2+\dots)^{-1}\\&=(x-\frac16x^3+\dots)\left[1+(-\frac12x^2+\dots)\right]^{-1}\\\end{align}\\本来是分母的，现在变成了负一次方，然后要干啥呢？回想多项式展开的第三个式子，是不是正是这种情况？刚接触、有些教条的同学可能想不明白，那不是 (1+x)^{-1} 的展开吗？这里又没有 x 。注意，这里的展开要求是什么？是 x→0 ，不是去展开一个形式上的“ x ”，而是去展开“一个趋于 0 的东西”。现在这里的 (-\frac12x^2+\dots) 是不是趋于 0 了呢？是，所以这里的展开就是：

\begin{align}\tan x&=(x-\frac16x^3+\dots)\left[1-(-\frac12x^2+\dots)+\dots\right]\\&=(x-\frac16x^3+\dots)(1+\frac12x^2+\dots)\\&=x-\frac16x^3+\frac12x^3+\dots\\&=x+\frac13x^3+\dots\end{align}\\这就是 \tan x 展开的前两项。可以发现，其第一项是和 \sin x 是一样的，都是 x ，是从第二项的系数开始变化。显然， \tan x 也是奇函数，所以下一项应该是 ?x^5 了，具体是什么，读者可以再多展开几项自己求一下看看。

\tan x 和 \sin x 在第二项一个减一个加，这当然就会在图像中体现出来。具体而言就是二者都与 y=x 相切，而随着 x 的增大， \tan x 是往上翘的，所以第二项是加； \sin x ​是往下弯的，所以第二项是减。

其他三角函数：

\sec x,\ \csc x,\ \cot x 都可以通过上面的函数取倒数的方式，利用 (1+x)^{-1} 将分母变相乘，则可以得到它们仨的展开。读者可以自己尝试推导。除此之外，在这里不加证明的给出两个反三角函数的展开。总的而言，可以得到这样的关系：

\begin{align}\arcsin x&=x{\color{red}{+}}\frac16x^3\quad\longleftarrow&\quad\sin x&=x-\frac16x^3\quad\longrightarrow&\quad\csc x&=\frac1x{\color{red}+}\frac16x\\{\color{blue}\arcsin x}&{\color{blue}+\arccos x=\frac\pi2\quad\longleftarrow}&\quad\cos x&=1-\frac12x^2\quad\longrightarrow&\quad\sec x&=1{\color{red}+}\frac12x^2\\\arctan x&=x{\color{red}{-}}\frac13x^3\quad\longleftarrow&\quad\tan x&=x+\frac13x^3\quad\longrightarrow&\quad\csc x&=\frac1x{\color{red}-}\frac13x\\\end{align}\\ 可以发现，除了蓝色的部分外，其余的都几乎只办了一件事：换符号。就是红色标出来的部分。项不变，系数不变，就换了个符号。

但是有两个是异类。一个是 \csc x 一个是 \cot x 。这俩居然有 \frac 1x ？这还是泰勒展开吗？泰勒展开有负幂次吗？

有 \frac1x 可以理解，由图就可以直接看出来：

其中蓝色的是 \csc x ，红色的是 \cot x 。这俩产生 \frac1x 的原因很简单。因为 \sin x,\ \tan x 这俩在 x=0 取值为 0 嘛，所以取倒数当然就会发散了。而发散的结果通过上面的推导可以推出来就是一个 \frac 1x 。至于记忆，则可以这么记： \sin x,\ \tan x 这俩系数不变、正负变号，然后它们的两项都除以 x^2 ，这样便“漏出”了 \frac 1x ，而 x^3 则变成了 x 。

至于这玩意还算不算泰勒展开…不用管，能用就行。这样的展开有另一个名字，读者可以在《复变函数》这们科目中自行了解。

最大的异类是那个蓝色的。蓝色的其实是出于反三角函数的关系：

\mathrm{arc}\text{正}+\mathrm{arc}\text{余}=\frac{\pi}2\\ 所以 \arcsin x 和 \arccos x 只要构造出一个的展开就行了。那，当然是构造 \arcsin x 的了。别问，问就是自己画 \arccos x ​的图去。

而 \mathrm{arccot} x,\ \mathrm{arcsec} x,\ \mathrm{arccsc} x ​的展开，建议不要接触…这方面是三角函数部分的内容，要说的话那对于泰勒展开来说有点超出范围了。感兴趣的同学可以自行学习反三角函数之间的关系，然后可以解锁一个“在无穷处进行泰勒展开”的技巧。

当我们学了三角函数的展开后，真的就只是在 x=0 处做展开吗？并非如此。比如 \cos x 的展开实际的含义是“对‘弦’的函数的极值点处做展开”， \cos x 在 x=0 是极值点，那 \sin x 在 x=\frac\pi 2 就不是极值点了吗？在这个点同样可以展开！只不过是需要做一点平移或者换元变换而已。对于切和割的函数同样也是如此。不要说我们知道了 \cot x 在 x=0 发散处的展开，却不知道 \tan x 在 x=\frac\pi2 发散处的展开，那就是不知道举一隅而不以三隅反了。

余下常用的麦克劳林展开还有 \ln (1+x) 的展开。不直接展开对数函数 \ln x 是因为其在 x=0 处的各阶导数都是 \pm\infty ，因此是不能写出展开式的：

\ln x=-\infty+\frac\infty1x-\frac\infty2x^2+\dots\\ 这样的表达是无意义的。

所以将其平移一格，让零点从 \ln x 的 x=1 变到 \ln(1+x) 的 x=0 。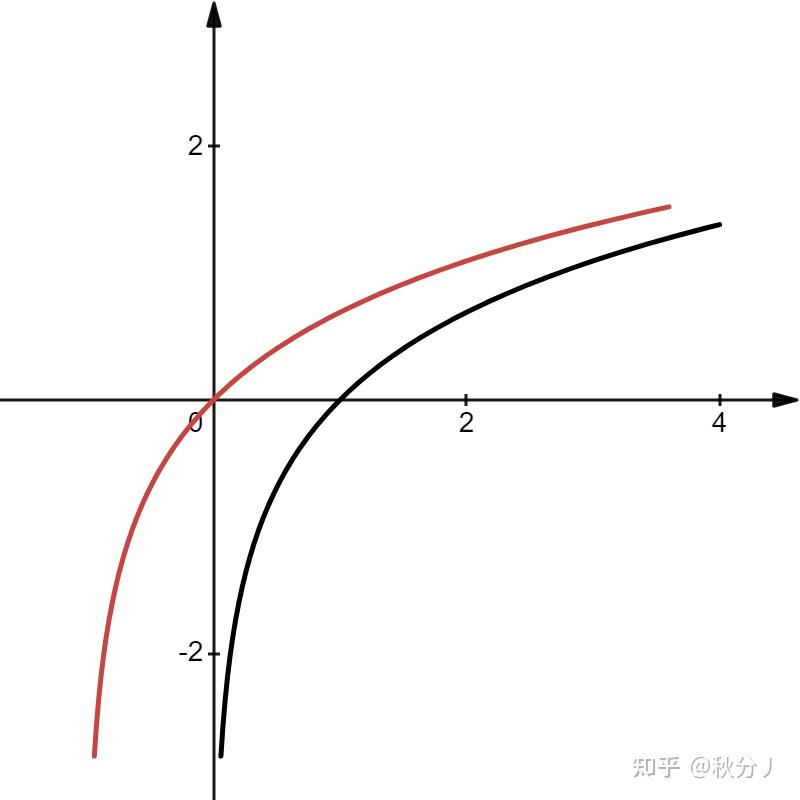

红色的是 \ln (1+x) ，黑色的是 \ln x 。

虽然展开 \ln (1+x) 可以视作对 \ln x 的平移，但还有另一种描述方式。

前面说的展开都是在 x=0 处做的展开，亦即麦克劳林展开。这个展开使用的多项式形如：

P(x)=a_0+a_1x+a_2x^2+\dots\\ 使用这样的多项式是有目的的，当然是为了在求 P^{(i)}(x) 的时候，带入 x=0 则可以消去 i!a_i+?\cdot0+?\cdot0^2+\dots 后面一连串的 0 。

那么现在，既然对于解析函数而言，只要一点处的导数就可以控制整个函数。那么我们现在不想在 x=0 处展开了，我们想在 x=x_0 处展开了，该当如何？

显然，如果还是用上面的 P(x) 的话，求 P^{(i)}(x) 带入 x=x_0 的时候是：

P^{(i)}(x)=i!a_i+?\cdot x_0^{i+1}+?\cdot x_0^{i+2}+\dots\\后面的那一串消不掉了，那就求不出 a_i 了。

为了能成功消掉后面的一串，可以将多项式换成：

P(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\dots\\这样一来，就有：

P^{(i)}(x)=i!a_i+?\cdot (x-x_0)^{i+1}+?\cdot(x-x_0)^{i+2}+\dots\\因此带入 x=x_0 之后，后面那一串就通过 (x_0-x_0)^n=0^n 和之前一样全部消掉了。这样以来就一样可以得到 a_i 的取值：

a_i=\frac{f^{(i)}(x_0)}{i!}\\此时的泰勒展开为：

f(x)=f(x_0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(x_0)}{i!}(x-x_0)^i}\\回想一下前面说的泰勒展开四部分，对比一下可以发现：

1、第一部分变了，从 f(0) 变成了 f(x_0) 。这是显然的嘛，在 x_0 展开当然首当其冲的就是函数值得相等啊。

2、求和里的三部分里分母是没变的，阶乘也没什么好变的嘛。

3、剩下两部分，分子显然的，在 x_0 展开当然是 f^{(i)}(x_0) 才对。

4、右边因为要在过程中要产生一大串的 0 ，当然要变成 (x-x_0) 的幂次。

稍微想一下就知道这是显然明了的东西。

但是在物理上或直白或含蓄的、实际上不太喜欢用这种形式。我们现在换一种表达。

注意两边的变量在哪里？左边的是在 f(x) 里面，右边的呢？再次注意，不是在分子上，分子上的那个 f 是固定了的。右边的变量在幂函数那里。

现在我们做一个变换： x-x_0=t ，那么泰勒展开就有另一种形式：

f(x_0+t)=f(x_0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(x_0)}{i!}t^i}\\咦，很明显的，右边变回了麦克劳林里的清清爽爽的纯正的幂次，没有什么 (x-x_0) 这种一看就很让人皱眉的形式了。但是左边变成了一个 f(x_0+t) ，这是什么意思？自变量是啥？

对于 f 来说，它作用的东西肯定是 (x_0+t) ，但是我们考察的变量却是 t 。这意味着什么呢？比如 f 作用到 3 上，得到 f(3) ，那现在假如我们是在 x_0=1 处展开的，那么这个变量 t 就应该取 t=2 。意思是：从展开点 x_0=1 开始，我们取了变量 t=2 ，得到了在 3 处的函数值 f(3) 。

那么 t 的意义就很明确了，意思是步长。这个展开的意义就更明确了，就是：

从展开点 x_0 出发，走了 t 的长度后，得到的函数值 f(x_0+t) ——其可以用右边、关于距离 t 的、幂函数的组合来描述。

所以第一项单独写出来就更有意味了：还没走呢，距离 t=0 ，那么这个点的值当然就是没走的 f(x_0) 。

这个 t 实际上是从 x_0 开始走的距离，这个距离不妨记作一个熟悉的符号 \Delta x ，那么就又可以写成：

f(x_0+\Delta x)=f(x_0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(x_0)}{i!}\Delta x^i}\\再画一下图：

那么这一堆求和所代表的含义就很清晰了。就是在这个距离里函数所变化的大小。那如果这一堆求和只取一项呢？

这第一项就是线性关系，也就是切线的增加幅度。同济课本里的“微分”里引入的那个“线性主部”就是这个东西。那剩下的、不线性的东西呢？哎，就是这整个求和其他的无限项啦。

所以同济课本里，用 \Delta y=A\Delta x+o(\Delta x) 来引入微分，有没有可能，用这样的方式来引入同学们会不会更好接受一点？

上面的是将距离记作 t,\ \Delta x ，但实际上这本身就是自变量。那就换回自变量最经典的 x 呗，换个符号而已。这样一来，就得到了 x 表达下的、 x_0 处泰勒展开的另一种表达：

f(x_0+x)=f(x_0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(x_0)}{i!}x^i}\\最初的也写在一起：

f(x)=f(x_0)+\sum_{i=1}^{\infty}{\frac{f^{(i)}(x_0)}{i!}(x-x_0)^i}\\两种都是在 x_0 处泰勒展开的表达。同学们喜欢或者具体需要使用哪一种就看需要了，反正我是喜欢增量的那种。并且 x_0=0 的麦克劳林展开也可以视为增量的形式。

现在再反回来看 \ln (1+x) 。显然，这可以认为是 \ln x 在 x_0=1 处的展开，并且是以增量形式给出的。或许这也是通常写成 \ln(1+x) 而不是 \ln(x+1) 的原因。具体而言有：

\ln(1+x)=x-\frac12x+\frac13x^2+\dots\\这里的记忆点就和前面的都不一样了。

泰勒展开三部分，分子分母幂函数。这里的分子依旧是 \pm 1 交替，幂函数还是幂函数，但是不一样的是，这个分母不是阶乘 i! 了，而是简单的 i 本身。

当然，也可以从 \frac1{1+x}=1-x+x^2+\dots 出发，积分一次，左边就得到了 \ln(1+x) ，右边就得到了展开关系。所以分母就是从积分而来的非常简单的 i 本身。

我们直到现在，写泰勒展开的时候都是以一个省略号结尾的，这代表了后面有无穷项的意思。虽然 f(x)\equiv P(x) 当然是需要无穷项才能完全的相等，但是我们使用的时候不可能真正的用到无穷项。我们使用多项式的时候都是用有限项，从无穷项到有限项就会有一个截断，截断之后就会产生一个后面那么多项不要了的偏差（这里的“偏差”是自然语言下的偏差，是刻意不引入如严格定义的“误差”等这样的词语的。）。

那么我们即想要用有限项的多项式，又不想要偏差怎么办？

那就在截断后再加一个余项 R ，意思是：这个项就代表着截断后的偏差了。

那么我们拿上前面的有限项，又带上这个余项，就既做到了有限，又做到了完全相等。

所以以下三种写法里：

\begin{align}f(x)&=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\dots\\f(x)&=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2\\f(x)&=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+R\end{align}\\只有第一种和第三种是正确的。第一种说明了无穷项；第三种截断了、但是加上了余项，所以二者都是左右两边完全的相等，可以写等号。而第二种右边从有限项就截断了，左右两边是不完全相等的，那么就不能写等于，应该只能写约等于。

关于 R 有两种：

第一种是“皮亚诺余项” o(x^n)

比如上面的第三种写法，写到了 x^2 项，则后面的皮亚诺余项就写成 o(x^2) ：

f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+o(x^2)\\这个余项的意思呢，是：后面的项阶数都比 x^2 大了，所以写个 x^2 的高阶项 o(x^2) 。但是具体这个偏差是多大是多少呢？不知道，不去管他，反正高阶就完事了——但是这个余项虽然我们具体写不出来，但是其精准等于截断后的偏差。所以这里左右两边是完全的等于，而不是约等于。

这也是有泰勒展开后应当抛弃掉所谓“等价无穷小”的方法一样。等价无穷小实际上就是泰勒展开后去掉后面的项，但是又没有给出余项的方法，所以只能用一个“ \sim ”连接。但是有泰勒展开了，我们是能够写得出确切的、完全相等的多项式化的表达的，那就可以抛弃等价无穷小这种完全不严谨的方法了。

另外需要注意的是，由于余项是只需要关注到展开的最高项 x^n ，那么更高的所有项都可以直接写到 o(x^n) 中。

所以不需要写什么 o(x^2+x^{3}) 这种写法，是没有必要的。同样的， o(x^2)+o(x^3)+o(x^4) 也都可以合并成 o(x^2) 。由于皮亚诺余项只关注阶数，因此系数也是没必要加上的， o(2x^2),\ 3o(x^2) 这样的表达都不要写出来，一样可以合并成 o(x^2) 就行了。

另一种余项是“拉格朗日余项” \frac{f^{(n+1)}(\xi)}{(n+1)!}x^{n+1}

上面的第三种可以写成：

f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(\xi)}{3!}x^{3}\\这个余项是啥意思呢？就是：再往后写一项，后面的所有偏差都浓缩在这个项中。

但是不对啊，如果能每一步都截出来、写出偏差，那比如上面，三阶就精确等于了，用三个完事了呗？

哪有这么好，真能有限项展开出来那还用研究 \sin x 这些函数干啥？直接用多项式不就完事了？这里看上去很美好，这是因为有一个不可确定的东西隐藏在了分子里。再写一项的这一项形式和前面是一样的：分子分母幂函数。但是分子的表达就不是在展开点了，而是 \xi 是在展开点 x_0=0 与自变量 x 这两值中间的某一点。具体是哪一点呢？不知道，反正就是某一点。

“某一点”这种东西是不可求的，所以这个误差项看上起很精确，但也和皮亚诺余项一样是一个形式上的误差项，是不能真正的求出来误差的。

但是拉格朗日余项好就好在它虽然不能精确求出来，但是至少给了一个代数的表达式，还有 \xi 具体的取值范围。那么就可以把余项视作 \xi 的函数，取个绝对值，就可以求出“这么截断后的偏差不大于多少”了。

如某个 f 在 x=0 的展开余项恒正，我们要求在 x=4 处的值，并且同时它对 \xi\in(0,4) 是单增的，那么带入上面的表达就有：

\left|\frac{f'''(\xi)}{3!}4^3\right|