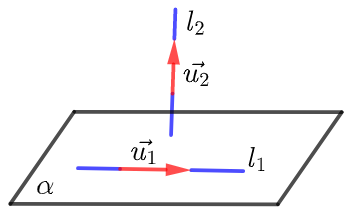
\({\color{Red}{欢迎到学科网下载资料学习 }}\) 【基础过关系列】高二数学上学期同步知识点剖析精品讲义(人教A版2019） \({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

选择性必修第一册同步巩固，难度2颗星！

设直线\(l_1\),\(l_2\)的方向向量分别是 \(\overrightarrow{u_{1}}\), \(\overrightarrow{u_{2}}\)，则要证明\(l_1⊥ l_2\)，只需证明 \(\overrightarrow{u_{1}} \perp \overrightarrow{u_{2}}\)，即 \(\overrightarrow{u_{1}} \cdot \overrightarrow{u_{2}}=0\) .

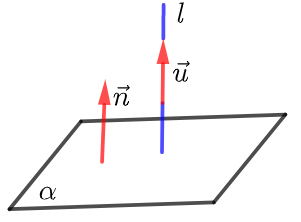
①(法一)设直线 \(l\)的方向向量是\(\vec{u}\)，平面α的法向量是\(\vec{n}\)，则要证明\(l⊥α\)，只需证明\(\vec{u}||\vec{n}\)，即\(\vec{u}=λ \vec{n}\).

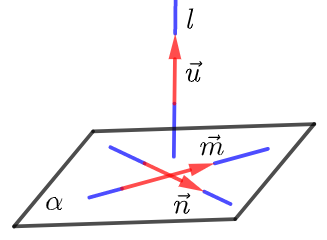
②(法二)设直线l的方向向量是\(\vec{u}\)，平面\(α\)内的两个相交向量分别为\(\vec{m}\),\(\vec{n}\)， 若 \(\left\{\begin{array}{l} \vec{u} \cdot \vec{m}=0 \\ \vec{u} \cdot \vec{n}=0 \end{array}\right.\)，则 \(l⊥α\).(即证明\(\vec{u}\)是平面\(α\)的法向量)

【例】已知直线\(l\)的方向向量为\(\vec{a}\)，平面α的法向量为\(\vec{n}\)，若\(\vec{a}=(-1,0,-1)\)，\(\vec{n} =(1,0,1)\)，则直线\(l\)与平面\(α\)(　　)   A．垂直 \(\qquad \qquad\) B．平行\(\qquad \qquad\) C．相交但不垂直 \(\qquad \qquad\) D．位置关系无法确定 解 若\(\vec{a}=(-1,0,-1)\)，\(\vec{n} =(1,0,1)\)，则\(\vec{a} =-\vec{n}\)，\(\vec{a} //\vec{n}\)，则直线\(l\)与平面\(α\)垂直，故选：\(A\)．  

若平面\(α\)的法向量为 \(\overrightarrow{n_{1}}\)，平面β的法向量为 \(\overrightarrow{n_{2}}\)，要证\(α⊥β\)， 只需证 \(\overrightarrow{n_{1}} \perp \overrightarrow{n_{2}}\)，即证 \(\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}=0\).

【例】若平面\(α\)与\(β\)的法向量分别是\(\vec{a} =(2,4,-3)\),\(\vec{b} =(-1,2,2)\)，判断平面\(α\)与\(β\)的位置关系. 解 \(\vec{a} ⋅\vec{b} =(2,4,-3)(-1,2,2)=-2+8－6=0\)，\(∴\vec{a} ⊥\vec{b}\) ，\(∴\)平面\(α\)与平面\(β\)垂直.  

【例】已知平面\(α\)，\(β\)的法向量分别为\(\vec{u} =(3,-1,4)\),\(\vec{v} =(-2,3,-5)\)，则(　　)  A．\(α//β\) \(\qquad \qquad\) B．\(α⊥β\) \(\qquad \qquad\) C．\(α，β\)相交但不垂直 \(\qquad \qquad\)D．\(α，β\)的位置关系不确定 解 平面\(α\)，\(β\)的法向量分别为\(\vec{u} =(3,-1,4)\),\(\vec{v} =(-2,3,-5)\)， 对于\(A\)， \(\because \dfrac{-2}{3} \neq \dfrac{3}{-1} \neq \dfrac{-5}{4}\)，\(∴α,β\)不平行，故\(A\)错误； 对于\(B\)， \(\vec{u} \cdot \vec{v}=-6-3-20=-29 \neq 0\)，\(∴α,β\)不垂直； 对于\(C\)，由\(A,B\)得\(α，β\)相交但不垂直，故\(C\)正确； 对于\(D\)，α，β相交但不垂直，故\(D\)错误． 故选：\(C\)．  

【典题1】 给出下列命题： ①直线\(l\)的方向向量为\(\vec{a}=(1,-1,2)\)，直线\(m\)的方向向量 \(\vec{b}=\left(2,1,-\dfrac{1}{2}\right)\)，则\(l\)与\(m\)垂直； ②直线\(l\)的方向向量 \(\vec{a}=(0,1,-1)\)，平面\(α\)的法向量 \(\vec{n}=(1,-1,-1)\)，则\(l⊥α\)； ③平面\(α\)、\(β\)的法向量分别为 \(\overrightarrow{n_{1}}=(0,1,3)\), \(\overrightarrow{n_{2}}=(1,0,2)\)，则\(α//β\)； ④平面\(α\)经过三点\(A(1,0,-1)\),\(B(0,1,0)\),\(C(-1,2,0)\)，向量 \(\vec{n}=(1, u, t)\)是平面\(α\)的法向量，则\(u+t=1\)． 其中真命题的是\(\underline{\quad \quad}\)．（把你认为正确命题的序号都填上） 解析 对于①，\(∵\vec{a} =(1,-1,2)\), \(\vec{b}=\left(2,1,-\dfrac{1}{2}\right)\)， \(\therefore \vec{a} \cdot \vec{b}=1 \times 2-1 \times 1+2 \times\left(-\dfrac{1}{2}\right)=0\)， \(\therefore \vec{a} \perp \vec{b}\)， \(∴\)直线\(l\)与\(m\)垂直，①正确； 对于②， \(\vec{a}=(0,1,-1)\)， \(\vec{n}=(1,-1,-1)\)， \(∴\vec{a}⋅\vec{n}=0×1+1×(-1)+(-1)×(-1)=0\)， \(∴\vec{a}⊥\vec{n}\)，\(∴l//α\)或\(l⊂α\)，②错误； 对于③， \(\because \overrightarrow{n_{1}}=(0,1,3)\), \(\overrightarrow{n_{2}}=(1,0,2)\)， \(\therefore \overrightarrow{n_{1}}\)与 \(\overrightarrow{n_{2}}\)不共线， \(∴α//β\)不成立，③错误； 对于④，\(∵\)点\(A(1,0,-1)\),\(B(0,1,0)\),\(C(-1,2,0)\)， \(\therefore \overrightarrow{A B}=(-1,1,1)\), \(\overrightarrow{B C}=(-1,1,0)\)， 向量\(\vec{n}=(1,u,t)\)是平面 的法向量， \(\therefore\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A B}=0 \\ \vec{n} \cdot \overrightarrow{B C}=0 \end{array}\right.\)，即 \(\left\{\begin{array}{l} -1+u+t=0 \\ -1+u=0 \end{array}\right.\)；则\(u+t=1\)，④正确． 综上，以上真命题的序号是①④．  

1.已知直线\(l_1\)的方向向量\(\vec{m}=(2,m,1)\)，\(l_2\)的方向向量 \(\vec{n}=\left(1, \dfrac{1}{2}, 2\right)\)，且\(l_2⊥l_1\)，则\(m=\)\(\underline{\quad \quad}\).  

2.已知直线\(l\)的一个方向向量\(\vec{a}=(1,2,m)\)，平面\(α\)的一个法向量 \(\vec{n}=(-1,-2,3)\)，若\(l⊥α\)，则\(m=\)\(\underline{\quad \quad}\) .  

3.已知平面\(α\)的一个法向量\(\vec{a}=(x,1,-2)\)，平面β的一个法向量 \(\vec{b}=\left(-1, y, \dfrac{1}{2}\right)\)，若\(α⊥β\)，则\(y-x=\)\(\underline{\quad \quad}\)．  

参考答案

答案 \(-8\) **解析 **\(∵\)直线\(l_1\)的方向向量\(\vec{m}=(2,m,1)\)，\(l_2\)的方向向量 \(\vec{n}=\left(1, \dfrac{1}{2}, 2\right)\)，且\(l_2⊥l_1\)， \(\therefore \vec{m} \cdot \vec{n}=2+\dfrac{1}{2} m+2=0\)，解得\(m=-8\)．

答案 \(-3\) 解析 \(∵\)直线\(l\)的一个方向向量\(\vec{a}=(1,2,m)\)，平面\(α\)的一个法向量 \(\vec{n}=(-1,-2,3)\)，\(l⊥α\)， \(∴\vec{a}//\vec{n}\)， \(\therefore \dfrac{-1}{1}=\dfrac{-2}{2}=\dfrac{3}{m}\)，解得\(m=-3\)．

答案 \(1\) 解析 \(∵\)面\(α\)的一个法向量\(\vec{a}=(x,1,-2)\)，平面β的一个法向量 \(\vec{b}=\left(-1, y, \dfrac{1}{2}\right)\)，\(α⊥β\)， \(\therefore \vec{a} \cdot \vec{b}=-x+y-1=0\)，解得\(y-x=1\)．

【典题1】 在长方体\(ABCD-A_1 B_1 C_1 D_1\)中，\(E\),\(F\)分别是棱\(BC\),\(CC_1\)上的点，\(CF=AB=2CE\)， \(AB:AD:AA_1=1:2:4\).证明\(AF⊥\)平面\(A_1 ED\). 解析 如图所示，建立空间直角坐标系，点\(A\)为坐标原点， 设\(AB=1\)，依题意得\(D(0,2,0)\),\(F(1,2,1)\),\(A_1 (0,0,4)\), \(E\left(1, \dfrac{3}{2}, 0\right)\) 已知 \(\overrightarrow{A F}=(1,2,1)\)， \(\overrightarrow{E A_{1}}=\left(-1,-\dfrac{3}{2}, 4\right)\)， \(\overrightarrow{E D}=\left(-1, \dfrac{1}{2}, 0\right)\)， 于是 \(\overrightarrow{A F} \cdot \overrightarrow{E A_{1}}=0\), \(\overrightarrow{A F} \cdot \overrightarrow{E D}=0\). 因此\(AF⊥EA_1\),\(AF⊥ED\)，又\(EA_1∩ED=E\)， 所以\(AF⊥\)平面\(A_1 ED\).  

【典题2】在如图所示的几何体中，四边形\(ABCD\)是正方形，\(MA⊥\)平面\(ABCD\)，\(PD//MA\)，\(E\),\(G\),\(F\)分别为\(MB\),\(PB\),\(PC\)的中点，且\(AD=PD=2MA\).求证：平面\(EFG⊥\)平面\(PDC\). 解析 以\(A\)为原点，向量 \(\overrightarrow{D A}, \overrightarrow{A B}, \overrightarrow{A M}\)分别为\(x\)轴、\(y\)轴、\(z\)轴的正方向，如图建立坐标系， 设\(AM=1\)，则\(AD=AB=PD=2\)， 则\(B(0，2，0)\)，\(C(-2，2，0)\)，\(D(-2，0，0)\)，\(P(－2，0，2)\)， \(M(0，0，1)\)， 则 \(\mathrm{E}\left(0,1, \dfrac{1}{2}\right)\)， \(\mathrm{G}(-1,1,1)\)， \(\mathrm{F}(-2,1,1)\)， \(\therefore \overrightarrow{E G}=\left(-1,0, \dfrac{1}{2}\right)\)， \(\overrightarrow{G F}=(-1,0,0)\)， 设平面\(EFG\)的法向量 \(\vec{m}=(x, y, z)\)， 则 \(\overrightarrow{E G} \cdot \vec{m}=-x+\dfrac{1}{2} z=0\)且 \(\overrightarrow{G F} \cdot \vec{m}=-x=0\)， 取\(y=1\)，则\(x=z=0\)， \(\therefore \vec{m}=(0,1,0)\)， 易证面\(PDC\)的法向量为 \(\overrightarrow{D A}=\left( 2, 0, 0\right)\)， \(\because \vec{m} \cdot \overrightarrow{D A}=2 \times 0+0 \times 1+0 \times 0=0\) \(\therefore \vec{m} \perp \overrightarrow{D A}\)， \(∴\)平面\(EFG⊥\)平面\(PDC\).  

1.已知三棱锥\(P－ABC\)中，\(PA⊥\)面\(ABC\)，\(AB⊥AC\)， \(\mathrm{PA}=\mathrm{AC}=\dfrac{1}{2} A B\)，\(N\)为\(AB\)上一点，\(AB=4AN\)，\(M\),\(S\)分别为\(PB\),\(BC\)的中点.证明：\(CM⊥SN\).  

2.如图，已知四棱锥\(P－ABCD\)的底面\(ABCD\)为等腰梯形，\(AB∥DC\)，\(AC⊥BD\)，\(AC\)与\(BD\)相交于点\(O\)，且顶点\(P\)在底面上的射影恰为\(O\)点，又\(BO=2\)， \(P O=\sqrt{2}\)，\(PB⊥PD\)．设点\(M\)在棱\(PC\)上，问\(M\)点在什么位置时，\(PC⊥\)平面\(BMD\)．  

3 在如图所示的几何体中，面\(CDEF\)为正方形，面\(ABCD\)为等腰梯形，\(AB∥CD\)，\(AB=2BC\)，\(∠ABC=60^∘\)，\(AC⊥FB\)． (1)求证：\(AC⊥\)平面\(FBC\)； (2)线段\(ED\)上是否存在点\(Q\)，使平面\(EAC⊥\)平面\(QBC\)？证明你的结论．  

参考答案

证明 设\(PA=1\)，以\(A\)为原点，射线\(AB,AC,AP\)分别为\(x,y,z\)轴正向建立空间直角坐标系如图， 则\(P(0,0,1)\)，\(C(0,1,0)\)，\(B(2,0,0)\)， \(M\left(1,0, \dfrac{1}{2}\right)\)， \(N\left(\dfrac{1}{2}, 0,0\right)\)， \(S\left(1, \dfrac{1}{2}, 0\right)\)， \(\overrightarrow{C M}=\left(1,-1, \dfrac{1}{2}\right)\), \(\overrightarrow{S N}=\left(-\dfrac{1}{2},-\dfrac{1}{2}, 0\right)\)， 因为 \(\overrightarrow{C M} \cdot \overrightarrow{S N}=-\dfrac{1}{2}+\dfrac{1}{2}+0=0\)， 所以\(CM⊥SN\).  

答案 \(M\)点是靠近\(C\)点的三等分点 解析 \(∵PO⊥\)平面\(ABCD\)，\(∴PO⊥BD\) 又\(PB⊥PD\)，\(BO=2\)， \(P O=\sqrt{2}\) 由平面几何知识得：\(OD=OC=1\)，\(BO=AO=2\) 以\(O\)为原点，\(OA\)，\(OB\)，\(OP\)分别为\(x,y,z\) 轴建立如图所示的空间直角坐标系， 则各点坐标为\(O(0,0,0)\)，\(A(2,0,0)\)，\(B(0,2,0)\)，\(C(－1,0,0)\)，\(D(0,－1,0)\)， \(P(0,0, \sqrt{2})\) 设\(M(x_0,0,z_0 )\)，由于\(P,M,C\)三点共线，得 \(\overrightarrow{P M} \| \overrightarrow{P C}\)， 即 \(\left(x_{0}, 0, z_{0}-\sqrt{2}\right) \|(-1,0,-\sqrt{2})\) 由对应系数成比例有 \(z_{0}=\sqrt{2} x_{0}+\sqrt{2}\)，则 \(M\left(x_{0}, 0, \sqrt{2} x_{0}+\sqrt{2}\right)\) \(∵PC⊥\)平面\(BMD\)， \(\therefore \overrightarrow{P C} \perp \overrightarrow{B M}\)， \(\therefore(-1,0,-\sqrt{2}) \cdot\left(x_{0},-2, \sqrt{2} x_{0}+\sqrt{2}\right)=0\)，得 \(x_{0}=-\dfrac{2}{3}\)， 所以 \(z_{0}=\dfrac{\sqrt{2}}{3}\)， \(\therefore M\left(-\dfrac{2}{3}, 0, \dfrac{\sqrt{2}}{3}\right)\)， 故 \(\dfrac{P M}{M C}=2\)，则\(M\)点是靠近\(C\)点的三等分点．  

答案 (1)略 (2)不存在 解析 (1)证明：\(∵AB=2BC\)，\(∠ABC=60°\)， 在\(△ABC\)中，由余弦定理可得\(AC^2=AB^2+BC^2－2AB\cdot BC\cos60°=3BC^2\)， \(∴AC^2+BC^2=4BC^2=AB^2\)，\(∴∠ACB=90°\)． \(∴AC⊥BC\)． 又\(∵AC⊥FB\)，\(FB∩BC=B\)， \(∴AC⊥\)平面\(FBC\)． (2)线段\(ED\)上不存在点\(Q\)，使平面\(EAC⊥\)平面\(QBC\)． 证明如下： 因为\(AC⊥\)平面\(FBC\)，所以\(AC⊥FC\)． 因为\(CD⊥FC\)，所以\(FC⊥\)平面\(ABCD\)． 所以\(CA,CF,CB\)两两互相垂直，如图建立的空间直角坐标系\(C－xyz\)． 在等腰梯形\(ABCD\)中，可得\(CB=CD\)． 设\(BC=1\)， 所以\(C(0,0,0)\), \(A(\sqrt{3}, 0,0)\),\(B(0,1,0)\)， \(D\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}, 0\right)\), \(E\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}, 1\right)\)． 所以\(\overrightarrow{C E}=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}, 1\right)\)， \(\overrightarrow{C A}=(\sqrt{3}, 0,0)\), \(\overrightarrow{C B}=(0,1,0)\)． 设平面\(EAC\)的法向量为 \(\vec{n}=(x, y, z)\)，则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{C E}=0 \\ \vec{n} \cdot \overrightarrow{C A}=0 \end{array}\right.\)， 所以 \(\left\{\begin{array}{l} \dfrac{\sqrt{3}}{2} x-\dfrac{1}{2} y+z=0 \\ \sqrt{3} x=0 \end{array}\right.\)，取\(z=1\)，得\(\vec{n}=(0,2,1)\)． 假设线段\(ED\)上存在点\(Q\)， 设 \(Q\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}, t\right)(0 \leq t \leq 1)\)，所以 \(\overrightarrow{C Q}=\left(\dfrac{\sqrt{3}}{2},-\dfrac{1}{2}, t\right)\)． 设平面\(QBC\)的法向量为\(\vec{m}=(a,b,c)\)，则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{C B}=0 \\ \vec{m} \cdot \overrightarrow{C Q}=0 \end{array}\right.\) 所以 \(\left\{\begin{array}{l} b=0 \\ \dfrac{\sqrt{3}}{2} a-\dfrac{1}{2} b+t c=0 \end{array}\right.\)，取\(c=1\)，得 \(\vec{m}=\left(-\dfrac{2 t}{\sqrt{3}}, 0,1\right)\)． 要使平面\(EAC⊥\)平面\(QBC\)，只需 \(\vec{m} \cdot \vec{n}=0\)， 即 \(-\dfrac{2}{\sqrt{3}} t \times 0+0 \times 2+1 \times 1=0\)，此方程无解． 所以线段\(ED\)上不存在点\(Q\)，使平面\(EAC⊥\)平面\(QBC\)．  

1 已知 \(\overrightarrow{v_{1}}, \overrightarrow{v_{2}}\)分别为直线\(l_1\),\(l_2\)的方向向量(\(l_1\),\(l_2\)不重合）， \(\overrightarrow{n_{1}}, \overrightarrow{n_{2}}\)分别为平面\(α\),\(β\)的法向量(\(α\),\(β\)不重合），则下列说法中不正确的是(　　)   A． \(\overrightarrow{v_{1}} / / \overrightarrow{v_{2}} \Leftrightarrow l_{1} / / l_{2}\) \(\qquad \qquad\) B． \(\overrightarrow{v_{1}} \perp \overrightarrow{n_{1}} \Leftrightarrow l_{1} / / \alpha\) \(\qquad \qquad\)C． \(\overrightarrow{n_{1}} \perp \overrightarrow{n_{2}} \Leftrightarrow \alpha \perp \beta\) \(\qquad \qquad\) D． \(\overrightarrow{n_{1}} // \overrightarrow{n_{2}} \Leftrightarrow \alpha / / \beta\)  

2 若直线\(l\)的方向向量为\((2,1,m)\)，平面\(α\)的法向量为 \(\left(1, \dfrac{1}{2}, 2\right)\)，且\(l⊥α\)，则\(m=\)(　　)  A．\(2\) \(\qquad \qquad\) B．\(3\) \(\qquad \qquad\) C．\(4\) \(\qquad \qquad\) D．\(5\)  

3已知平面\(α\)内的两个向量 \(\vec{a}=(1,1,1)\)， \(\vec{b}=(0,2,-1)\)，且 \(\vec{c}=m \vec{a}+n \vec{b}+(4,-4,1)\)．若 \(\vec{c}\)为平面\(α\)的法向量，则\(m,n\)的值分别为(　　)  A．\(－1,2\) \(\qquad \qquad\) B．\(1,－2\)\(\qquad \qquad\) C．\(1,2\) \(\qquad \qquad\) D．\(－1,－2\)   4已知平面\(α\)的法向量是 \(\vec{a}=(3 x-1,-1, x+5)\)，平面\(β\)的法向量是 \(\vec{b}=\left(x+1, x^{2}+3,-x\right)\)，且\(α⊥β\)，则实数\(x\)的值为\(\underline{\quad \quad}\)．

5在边长是\(2\)的正方体\(ABCD－A_1 B_1 C_1 D_1\)中，\(E\)，\(F\)分别为\(AB\)，\(A_1 C\)的中点．应用空间向量方法求解下列问题． (1)求\(EF\)的长；(2)证明：\(EF∥\)平面\(AA_1 D_1 D\)；(3)证明：\(EF⊥\)平面\(A_1 CD\)．  

6 如图，在直三棱柱\(ABC－A_1 B_1 C_1\)中，\(AB⊥AC\)，\(AB=AC=AA_1\)，\(D\)为\(BC\)的中点． (1)证明：\(A_1 B//\)平面\(ADC_1\)；(2)证明：平面\(ADC_1⊥\)平面\(BB_1 C_1 C\)．  

7 如图\(1\)，在\(Rt△ABC\)中，\(∠C=90°\)，\(BC=3\)，\(AC=6\)，\(D\)，\(E\)分别是\(AC\)，\(AB\)上的点，且\(DE∥BC\)，\(DE=2\)，将\(△ADE\)沿\(DE\)折起到\(△A_1 DE\)的位置，使\(A_1 C⊥CD\)，如图\(2\)． (1)求证：\(A_1 C⊥\)平面\(BCDE\)； (2)线段\(BC\)上是否存在点\(P\)，使平面\(A_1 DP\)与平面\(A_1 BE\)垂直？说明理由．    

参考答案

答案 \(B\) 解析 对于选项\(A\)：因为\(l_1\),\(l_2\)不重合，所以 \(\overrightarrow{v_{1}} / / \overrightarrow{v_{2}} \Leftrightarrow l_{1} / / l_{2}\)，故选项\(A\)正确， 对于选项\(B\)：若 \(\overrightarrow{v_{1}} \perp \overrightarrow{n_{1}}\)，则有可能\(l_1⊆α\)，故选项\(B\)错误， 对于选项\(C\)：因为\(α\),\(β\)不重合，所以 \(\overrightarrow{n_{1}} \perp \overrightarrow{n_{2}} \Leftrightarrow \alpha \perp \beta\)，故选项\(C\)正确， 对于选项\(D\)：因为\(α\),\(β\)不重合，所以 \(\overrightarrow{n_{1}} // \overrightarrow{n_{2}} \Leftrightarrow \alpha / / \beta\)，故选项\(D\)正确， 故选：\(B\)．

答案 \(C\) 解析 \(∵\)直线\(l\)的方向向量为\((2,1,m)\)，平面\(α\)的法向量为 \(\left(1, \dfrac{1}{2}, 2\right)\)，且\(l⊥α\)， \(∴l\)的方向向量为\((2,1,m)\)与平面\(α\)的法向量为 \(\left(1, \dfrac{1}{2}, 2\right)\)平行， \(\therefore(2,1, m)=\lambda\left(1, \dfrac{1}{2}, 2\right)\)． \(\therefore\left\{\begin{array}{l} 2=\lambda \\ 1=\dfrac{1}{2} \lambda \\ m=2 \lambda \end{array}\right.\)，解得\(m=4\)．故选：\(C\)．

答案 \(A\) 解析 \(∵\vec{a}=(1,1,1)\)， \(\vec{b}=(0,2,-1)\)， \(\therefore \vec{c}=m \vec{a}+n \vec{b}+(4,-4,1)=(m, m, m)+(0,2 n,-n)+(4,-4,1)\) \(=(m+4,m+2n－4,m－n+1)\)． 由 \(\vec{c}\)为平面\(α\)的法向量，得 \(\left\{\begin{array}{l} \vec{c} \cdot \vec{a}=3 m+n+1=0 \\ \vec{c} \cdot \vec{b}=m+5 n-9=0 \end{array}\right.\)，解得 \(\left\{\begin{array}{l} m=-1 \\ n=2 \end{array}\right.\)． 故选：\(A\)．

答案 \(－1\)或\(4\) 解析 \(∵α⊥β\)， \(\therefore \vec{a} \perp \vec{b}\)， \(\therefore \vec{a} \cdot \vec{b}=(3 x-1)(x+1)-\left(x^{2}+3\right)-x(x+5)=0\)，解得\(x=－1\)或\(4\)．

答案 (1) \(\sqrt{2}\) (2)略 (3)略 解析 (1)如图建立空间直角坐标系， 则\(A_1 (2,0,2)\),\(A(2,0,0)\),\(B(2,2,0)\)，\(C(0,2,0)\),\(D_1 (0,0,2)\),\(D(0,0,0)\)， \(∵E,F\)分别为\(AB,A_1 C\)的中点，\(∴E(2,1,0)\)，\(F(1,1,1)\)， \(\overrightarrow{E F}=(-1,0,1)\)， \(\therefore|\overrightarrow{E F}|=\sqrt{1+0+1}=\sqrt{2}\)． (2) \(\because \overrightarrow{A D}_{1}=(-2,0,2)=2 \overrightarrow{E F}\)，\(∴EF//AD_1\)， 又\(AD_1⊂\)平面\(AA_1 D_1 D\)，\(EF⊄\)平面\(AA_1 D_1 D\)， \(∴EF∥\)平面\(AA_1 D_1 D\)． (3) \(\overrightarrow{C D}=(0,-2,0)\)， \(\overrightarrow{A_{1} D}=(-2,0,-2)\)， \(\because \overrightarrow{C D} \cdot \overrightarrow{E F}=0\)， \(\overrightarrow{E F} \cdot \overrightarrow{A_{1} D}=0\)， \(∴EF⊥CD\)，\(EF⊥A_1 D\)，又\(CD∩A_1 D=D\)， \(∴EF⊥\)平面\(A_1 CD\)．

证明 (1)证明：\(∵\)在直三棱柱\(ABC－A_1 B_1 C_1\)中，\(AB⊥AC\)， \(∴\)以\(A_1\)为原点，\(A_1 C_1\)为\(x\)轴，\(A_1 B_1\)为\(y\)轴，\(A_1 A\)为\(z\)轴，建立空间直角坐标系， 设\(AB=AC=AA_1=2\)， \(A_1 (0,0,0)\)，\(B(0,2,2)\)，\(A(0,0,2)\)，\(C(2,0,2)\)，\(D(1,1,2)\)，\(C_1 (2,0,0)\)， \(\overrightarrow{A_{1} B}=(0,2,2)\)， \(\overrightarrow{A D}=(1,1,0)\)， \(\overrightarrow{A C}_{1}=(2,0,-2)\)， 设平面\(ADC_1\)的法向量 \(\vec{n}=(x, y, z)\)， 则 \(\left\{\begin{array}{l} \vec{n} \cdot \overrightarrow{A D}=x+y=0 \\ \vec{n} \cdot \overrightarrow{A C_{1}}=2 x-2 z=0 \end{array}\right.\)，取\(x=1\)，得\(\vec{n}=(1,－1,1)\)， \(\because \vec{n} \cdot \overrightarrow{A_{1} B}=0-2+2=0\)，且\(A_1 B⊄\)平面\(ADC_1\)， \(∴A_1 B∥\)平面\(ADC_1\)． (2)证明： \(\because \overrightarrow{D C}=(1,-1,0)\)， \(\overrightarrow{D C}_{1}=(1,-1,-2)\)， 设平面\(BB_1 C_1 C\)的法向量 \(\vec{m}=(a, b, c)\)， 则 \(\left\{\begin{array}{l} \vec{m} \cdot \overrightarrow{D C}=a-b=0 \\ \vec{m} \cdot \overrightarrow{D C_{1}}=a-b-2 c=0 \end{array}\right.\)，取\(a=1\)，得\(\vec{m}=(1,1,0)\)， 又平面\(ADC_1\)的法向量 \(\vec{n}=(1,－1,1)\)， \(\therefore \vec{n} \cdot \vec{m}=1-1+0=0\)， \(∴\)平面\(ADC_1⊥\)平面\(BB_1 C_1 C\)．

答案 (1) 略 (2) 不存在 解析 (1)证明：\(∵CD⊥DE\)，\(A_1 D⊥DE\)，\(CD∩A_1 D=D\)， \(∴DE⊥\)平面\(A_1 CD\)， 又\(∵A_1 C⊂\)平面\(A_1 CD\)，\(∴A_1 C⊥DE\)， 又\(A_1 C⊥CD\)，\(CD∩DE=D\)， \(∴A_1 C⊥\)平面\(BCDE\) (2)解：如图建系， 则\(C(0,0,0)\)，\(D(－2,0,0)\)， \(A_{1}(0,0,2 \sqrt{3})\)，\(B(0,3,0)\)，\(E(－2,2,0)\)， 设线段\(BC\)上存在点\(P\)，设\(P\)点坐标为\((0,a,0)\)，则\(a∈[0,3]\)， \(\therefore \overrightarrow{A_{1} P}=(0, a,-2 \sqrt{3})\)， \(\overrightarrow{D P}=(2, a, 0)\)， 设平面\(A_1 DP\)法向量为 \(\overrightarrow{n_{1}}=\left(x_{1}, y_{1}, z_{1}\right)\)， 则 \(\left\{\begin{array}{l} a y_{1}-2 \sqrt{3} z_{1}=0 \\ 2 x_{1}+a y_{1}=0 \end{array}\right.\)， \(\therefore\left\{\begin{array}{l} z_{1}=\dfrac{\sqrt{3}}{6} a y_{1} \\ x_{1}=-\dfrac{1}{2} a y_{1} \end{array}\right.\)， \(\therefore \overrightarrow{n_{1}}=(-3 a, 6, \sqrt{3} a)\)， 假设平面\(A_1 DP\)与平面\(A_1 BE\)垂直，则 \(\sqrt{n_{1}} \cdot \vec{n}=0\)， \(∴3a+12+3a=0\)，\(6a=－12\)，\(a=－2\) \(∵0≤a≤3\)， \(∴\)不存在线段\(BC\)上存在点\(P\)，使平面\(A_1 DP\)与平面\(A_1 BE\)垂直.

1 已知直线\(l\)的一个方向向量为\(\vec{a}=(m,1,3)\)，平面\(α\)的一个法向量为\(\vec{b}=(-2,n,1)\)，现给出下列结论： ①若\(l//α\)，则\(2m-n=3\)；②若\(l⊥α\)，则\(2m-n=3\)； ③若\(l//α\)，则\(mn+2=0\)；④若\(l⊥α\)，则\(mn+2=0\)． 其中所在正确结论的序号是(　　)  A．①③ \(\qquad \qquad\) B．①④ \(\qquad \qquad\) C．②③ \(\qquad \qquad\) D．②④  

2 (多选)已知点\(P\)是平行四边形\(ABCD\)所在的平面外一点，如果 \(\overrightarrow{A B}=(2,-1,-4)\)， \(\overrightarrow{A D}=(4,2,0)\)， \(\overrightarrow{A P}=(-1,2,-1)\)，下列结论正确的有 (　　)  A．\(AP⊥AB\) \(\qquad \qquad\) B．四边形\(ABCD\)为矩形 \(\qquad \qquad\) C． \(\overrightarrow{A P}\)是平面\(ABCD\)的一个法向量 \(\qquad \qquad\) D． \(\overrightarrow{A P} / / \overrightarrow{B D}\)  

3 在三棱锥\(P－ABC\)中，\(PB⊥\)平面\(ABC\)，\(AB⊥BC\)，\(AB=PB=2\)， \(B C=2 \sqrt{3}\)，\(E、G\)分别为\(PC\)、\(PA\)的中点．   (1)求证：平面\(BCG⊥\)平面\(PAC\)；   (2)在线段\(AC\)上是否存在一点\(N\)，使\(PN⊥BE\)？证明你的结论．    

参考答案

答案 \(B\) 解析 直线\(l\)的一个方向向量为\(\vec{a}=(m,1,3)\)，平面\(α\)的一个法向量为 \(\vec{b}=(-2,n,1)\)， 对于①，若\(l//α\)，则\(\vec{a}⋅\vec{b}=-2m+n+3=0\)，\(∴2m-n=3\)，故①正确； 对于②，若\(l⊥α\)，则\(\vec{a}//\vec{b}\)， \(\therefore \dfrac{m}{-2}=\dfrac{1}{n}=\dfrac{3}{1}\)，解得 \(m=-6, n=\dfrac{1}{3}\)， \(\therefore 2 m-n=-\dfrac{37}{3}\)，故②错误； 对于③，若\(l//α\)，则\(\vec{a}⋅\vec{b}=-2m+n+3=0\)，\(∴n=2m-3\)， \(m n+2=2 m^{2}-3 m+2=2\left(m-\dfrac{3}{4}\right)^{2}+\dfrac{7}{8} \geqslant \dfrac{7}{8}\)，故\(C\)错误； ④若\(l⊥α\)，则 \(\dfrac{m}{-2}=\dfrac{1}{n}=\dfrac{3}{1}\)，解得 \(m=-6, n=\dfrac{1}{3}\)，\(∴mn+2=0\)，故④正确． 故选：\(B\)

答案 \(AC\) 解析 对于\(A\)， \(\overrightarrow{A B} \cdot \overrightarrow{A P}=2 \times(-1)+(-1) \times 2+(-4) \times(-1)=0\)， 所以 \(\overrightarrow{A B} \perp \overrightarrow{A P}\)，即\(AP⊥AB\)，故选项\(A\)正确； 对于\(B\)，题中没有相关条件可以判断四边形\(ABCD\)是否为矩形，故选项\(B\)错误； 对于\(C\)， \(\overrightarrow{A P} \cdot \overrightarrow{A D}=(-1) \times 4+2 \times 2+(-1) \times 0=0\)，所以 \(\overrightarrow{A P} \perp \overrightarrow{A D}\)， 又 \(\overrightarrow{A B} \perp \overrightarrow{A P}\)，所以 \(\overrightarrow{A P}\)是平面\(ABCD\)的一个法向量，故选项\(C\)正确； 对于\(D\)，因为 \(\overrightarrow{A P}\)是平面\(ABCD\)的一个法向量，则 \(\overrightarrow{A P} \perp \overrightarrow{B D}\)，故选项\(D\)错误． 故选：\(AC\)．

答案 (1) 略 (2) 存在 解析 (1)\(∵PB⊥\)平面\(ABC\)，\(BC⊂\)平面\(ABC\)，\(∴BC⊥PB\)， 又\(AB⊥BC\)，\(AB∩BP=B\)， \(∴BC⊥\)平面\(PAB\)，\(PA⊂\)平面\(PAB\)， \(∴BC⊥PA\)．① 又\(AB=PB=2\)，\(△PAB\)为等腰直角三角形，\(G\)为斜边\(PA\)的中点， \(∴BG⊥PA\)，②又\(BG∩BC=B\)， \(∴PA⊥\)平面\(BCG\)，\(PA⊂\)平面\(PAC\)， \(∴\)平面\(BCG⊥\)平面\(PAC\)； (2)以点\(B\)为坐标原点，\(BA\)为\(x\)轴，\(BC\)为\(y\)轴，\(BP\)为\(z\)轴建立空间直角坐标系， 则\(A(2,0,0)\), \(C(0,2 \sqrt{3}, 0)\),\(P(0,0,2)\), \(E(0, \sqrt{3}, 1)\)， 设存在点\(N∈AC\)，使\(PN⊥BE\)，点\(N\)的坐标设为\(N(x_0,y_0,0)\) 则：得 \(\overrightarrow{B E}=(0, \sqrt{3}, 1)\), \(\overrightarrow{P N}=\left(x_{0}, y_{0},-2\right)\) 由相似三角形得： \(\dfrac{2-x_{0}}{|A B|}=\dfrac{y_{0}}{|B C|}\)，即 \(\dfrac{2-x_{0}}{2}=\dfrac{y_{0}}{2 \sqrt{3}}\)， \(\therefore y_{0}=2 \sqrt{3}-\sqrt{3} x_{0}\)． \(\therefore \overrightarrow{P N}=\left(x_{0}, 2 \sqrt{3}-\sqrt{3} x_{0},-2\right)\) 又\(PN⊥BE\)， \(\therefore \overrightarrow{B E} \cdot \overrightarrow{P N}=0\)． \(\therefore 0 \times x_{0}+\sqrt{3} \times\left(2 \sqrt{3}-\sqrt{3} x_{0}\right)+1 \times(-2)=0\)， \(\therefore x_{0}=\dfrac{4}{3} \in[0,2]\)，故存在点\(N∈AC\)，使\(PN⊥BE\)．

1 如图\(1\)所示，在边长为\(12\)的正方形\(AA' A_1' A_1\)中，点\(B\)，\(C\)在线段\(AA'\)上，且\(AB=3\)，\(BC=4\)，作\(BB_1∥AA_1\)，分别交\(A_1 A_1'\)、\(AA_1'\)于点\(B_1\) 、\(P\)，作\(CC_1∥AA_1\)，分别交\(A_1 A_1'\) 、\(AA_1'\)于点\(C_1\)、\(Q\)，将该正方形沿\(BB_1\)、\(CC_1\)折叠，使得 \(A^{\prime} A_{1}{ }^{\prime}\)与\(AA_1\)重合，构成如图\(2\)所示的三棱柱\(ABC－A_1 B_1 C_1\)． (1)在三棱柱\(ABC－A_1 B_1 C_1\)中，求证：\(AB⊥\)平面\(BCC_1 B_1\)； (2)求平面\(APQ\)将三棱柱\(ABC－A_1 B_1 C_1\)分成上、下两部分几何体的体积之比； (3)试判断直线\(AQ\)是否与平面\(A_1 C_1 P\)平行，并说明理由．    

参考答案