【分享】Cocos Creator 向量基础及其使用

您所在的位置：网站首页 › 法向量的运算 › 【分享】Cocos Creator 向量基础及其使用

【分享】Cocos Creator 向量基础及其使用

2024-07-15 23:17| 来源: 网络整理| 查看: 265

原文地址：https://www.jianshu.com/p/7e18f6a4d6e3 原文地址的数学公式MathJax的渲染会更加合理好看前言在某一次Cocos的线下沙龙中，有大佬推荐了 Games 101 的课程，去观摩了，发现十分收益，因此就有了这次的文章，或者更多是个人笔记以下内容主要来自 Games 101 第二节课 https://www.bilibili.com/video/BV1X7411F744?p=2 个人在这个基础上，在结合 Cocos Creator 进行的一些个人理解及理论实例使用一、向量归一化

向量 $\vec a$ 的归一化表示得到一个方向和向量 $\vec a$ 相同的向量，但是向量的模（向量的长度）为 1 。

归一化后的向量，也被叫作单位向量。

二、向量点乘

向量点乘公式：

$\vec a \cdot \vec b = \lvert a \rvert \lvert b \rvert cos \theta$

向量点乘满足一般运算规则：

交换律： $\vec a \cdot \vec b = \vec b \cdot \vec a$ 结合律： $\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c$ 分配律： $(k \vec a) \cdot \vec b = \vec a \cdot (k \vec b)$

直角坐标系下，在二维空间下，计算点乘：

$\vec a \cdot \vec b = {x_a \choose y_a} \cdot {x_b \choose y_b} = x_a x_b + y_a y_b$

直角坐标系下，在三维空间下，计算点乘：

$\vec a \cdot \vec b = \begin{pmatrix}x_a \\ y_a \\ z_a\end{pmatrix} \cdot \begin{pmatrix}x_b \\ y_b \\ z_b\end{pmatrix} = x_a x_b + y_a y_b + z_a + z_b$

根据点乘公式，我们知道，向量点乘是一个数，那么这个数在图形学上的几何意义是什么呢？

2.1 计算两个向量之间的夹角

根据向量点乘公式，我们可以推导出：

$cos \theta = \frac {\vec a \cdot \vec b}{\lvert a \rvert \lvert b \rvert}$

如果将向量 $\vec a$ 和向量 $\vec b$ 进行归一化，那么 $\lvert a \rvert \lvert b \rvert = 1$ ，可以在推导出

$cos \theta = \vec a \cdot \vec b$

根据 $cos \theta$ ，我们就可以知道两个向量之间的夹角（角度） $[0^\circ,180^\circ]$ 。

整理一下，在实际的计算中，过程如下：

将两个向量归一化计算归一化后的向量的点乘结果

GLSL 中可以表示为：

vec3 a; vec3 b; float c = dot(normalize(a), normalize(b)); 2.2 判断两个向量前后（方向）

利用点乘我们可以知道两个方向之间的夹角：

$cos \theta = \frac {\vec a \cdot \vec b}{\lvert a \rvert \lvert b \rvert}$

根据余弦函数的曲线图，我们可以知道

当 $\theta = 0^\circ$ 时， $cos\theta = 0$ 当 $0 \theta 90^\circ$ 时， $0 cos\theta 1$ 当 $\theta = 90^\circ$ 时， $cos\theta = 1$ 当 $90 \theta 180^\circ$ 时， $-1 cos\theta 0$ 当 $\theta = 180^\circ$ 时， $cos\theta = -1$

也就是说

$\vec a \cdot \vec b = 0$ ，向量 $\vec a$ 和向量 $\vec b$ 方向完全一致 $0 \vec a \cdot \vec b 1$ ，向量 $\vec a$ 和向量 $\vec b$ 方向基本一致 $\vec a \cdot \vec b = 1$ ，向量 $\vec a$ 和向量 $\vec b$ 方向垂直 $-1 \vec a \cdot \vec b 0$ ，向量 $\vec a$ 和向量 $\vec b$ 方向基本相反 $\vec a \cdot \vec b = -1$ ，向量 $\vec a$ 和向量 $\vec b$ 方向完全相反

根据这个数值，我们可以得出，向量 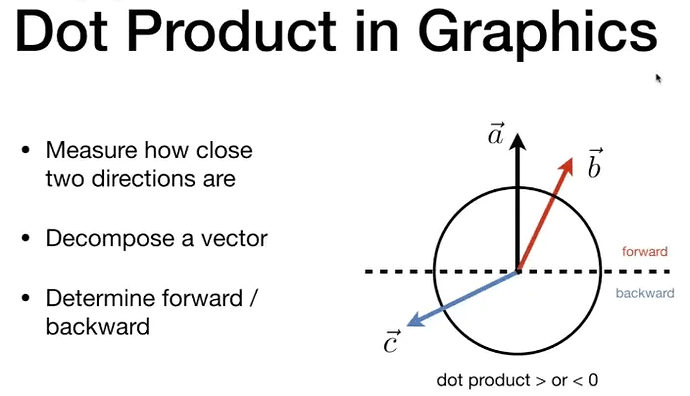$\vec a$ 和向量 $\vec b$ 的前后关系：

image704×405 76.6 KB

利用这个几何意义，可以实现：

3D内发光：见论坛大佬搬砖小菜鸟的shader例子中的3D内发光实现，以下为大佬的演示图： 640

2.3 计算向量投影

计算向量 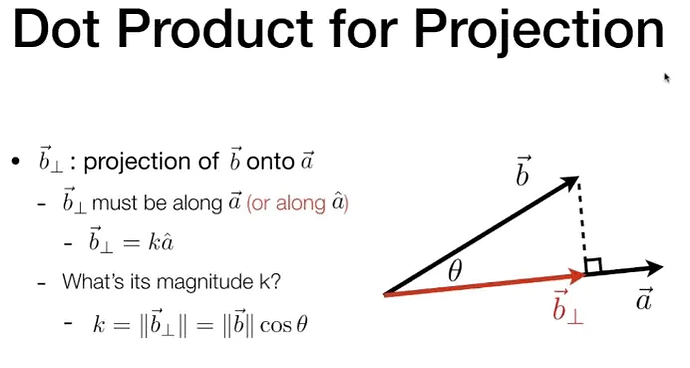$\vec b$ 在向量 $\vec a$ 上的投影向量：

image692×370 65.9 KB

得到投影后，还可以在进一步分解向量 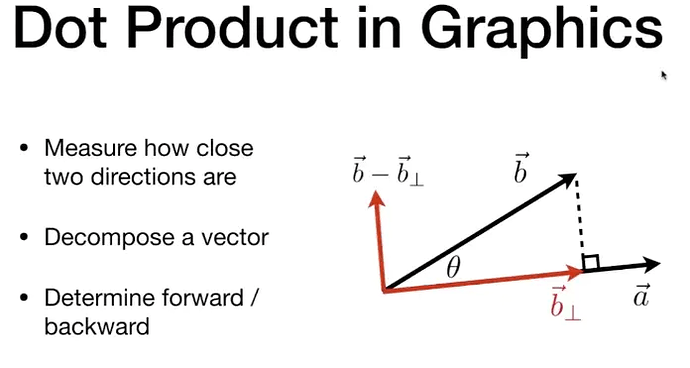$\vec b$ ：

image696×372 68 KB 三、向量叉乘

向量叉乘公式：

$\vec a \times \vec b = \begin{pmatrix}y_a z_b - y_b z_a \\ z_a x_b - x_a z_b \\ x_a y_b - y_a x_b\end{pmatrix}$

GLSL 中可以表示为：

vec3 a; vec3 b; vec3 c = cross(a, b);

ps:叉乘的结果是一个向量，点乘是得到一个数

3.1 计算法线向量

向量 $\vec a$ 和向量 $\vec b$ 的叉乘得到的是一个同时垂直于向量 $\vec a$ 和向量 $\vec b$ 的向量 $\vec c$

只要向量 $\vec a$ 和向量 $\vec b$ 的夹角不为 $0^\circ$ 和 $180^\circ$ ，那么向量 $\vec a$ 和向量 $\vec b$ 可以组成一个平面，而向量 $\vec a$ 和向量 $\vec b$ 的叉乘就得到一个垂直于这个平面的向量，这个向量也叫法向量。

垂直于一个平面的向量，方向有两个，并且这两个方向完全相反。为了准确得到方向，我们可以采用右手螺旋定则。

当为 $\vec a \times \vec b$ 时：伸出左手，摆出点赞姿势，左手握住向量 $\vec b$ ，左手拇指指向向量 $\vec b$ 的方向，此时其余四个手指握拳姿势，按着这4个手指的指向姿势，绕着拇指旋转 $90^\circ$ ，得到的新向量即为 $\vec a \times \vec b$ 的结果向量当为 $\vec b \times \vec a$ 时：此时则为左手握住向量 $\vec a$ 旋转

操作下来可以发现，两次叉乘得到的新向量，方向完全相反，但是大小（长度）是一致的，于是有：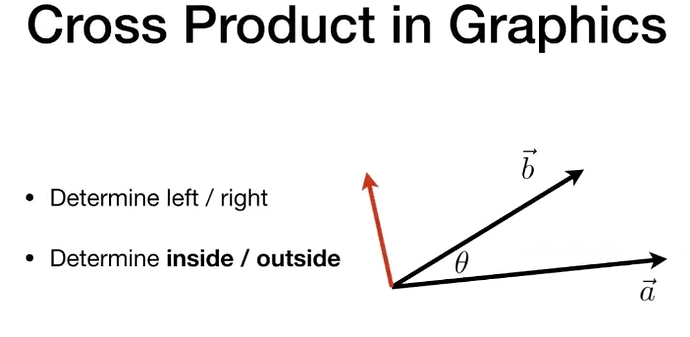

$\vec a \times \vec b = -\vec b \times \vec a$

3.2 判断向量的左右

image703×344 48.6 KB

假设向量 $\vec a$ 向量 $\vec b$ 都在 xy 的二维平面上，并假设 $\vec a \times \vec b = \vec c$ 。那么

$\vec c = \vec a \times \vec b = \begin{pmatrix}y_a z_b - y_b z_a \\ z_a x_b - x_a z_b \\ x_a y_b - y_a x_b\end{pmatrix}$

因为二维平面上，向量 $\vec a$ 和向量 $\v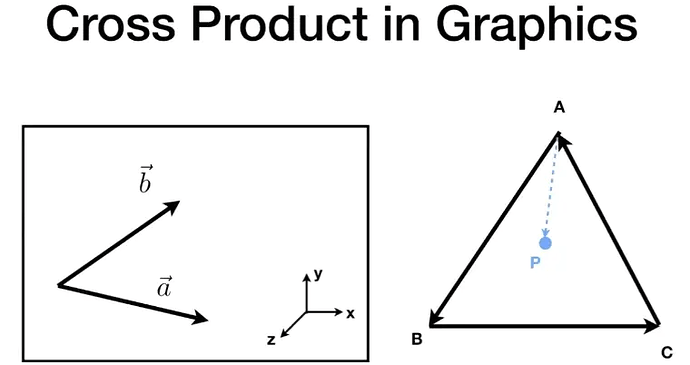ec b$ 的 $z$ 肯定为 $0$ ，所以

$\vec c = \begin{pmatrix}0 \\ 0 \\ x_a y_b - y_a x_b\end{pmatrix}$

根据右手螺旋定则， $\vec a \times \vec b$ 表示，法向量 $\vec c$ 是绕向量 $\vec a\vec b$ 所在平面旋转得到的，这里可以定义

$\vec c$ 的 z 值为正，则表示向量 $\vec a$ 在向量 $\vec b$ 的右侧 $\vec c$ 的 z 值为负，则表示向量 $\vec a$ 在向量 $\vec b$ 的左侧 3.2.1 判断点在多边形内部还是外部

image760×403 48.3 KB

以上图为例，在刚才左右的基础上，如果

向量 $\vec {AP}$ 在向量 $\vec {AB}$ 的左边向量 $\vec {BP}$ 在向量 $\vec {BC}$ 的左边向量 $\vec {CP}$ 在向量 $\vec {CA}$ 的左边

那么，点 $P$ 在三角线 ABC 内。

这样子通过叉乘就可以知道点是否在三角形内/外，这也是光栅化的基础，判断点是否在三角形内。

更进一步，我们还可以通过向量叉乘来判断点是否在多边形内。

比如：

Cocos Creator 提供的 cc.Intersection.pointInPolygon 方法，其内部原理是通过向量叉乘来判断点是否在多边形内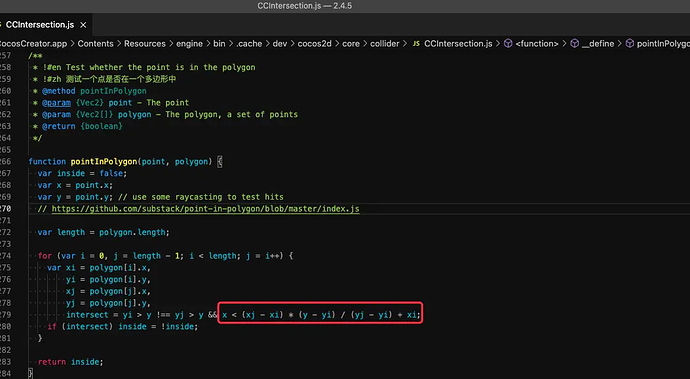

image1053×579 119 KB SVG 的填充属性 fill-rule： evenodd（奇偶填充）和 nonzero（非零填充），其内部实现我猜应该也是可以通过向量叉乘来解决 3.2.2 画多边形

既然知道了向量叉乘可以判断点是否在多边形内外，那么我们也可以根据这个几何意义去画任意多边形。以六边形为例：

标注及代码如下：

/** * 画六边形 * @param center 中心点 * @param side 六边形边长 * @param color 六边形颜色 */ vec4 drawHex(vec2 center, float side, vec4 color) { // 将uv往六边形中心点偏移，实现偏移后的坐标系原点在纹理中心，x 向右 y 向下 // 并转换为我们需要判断的点 vec2 uv = v_uv0.xy - center; vec3 p = vec3(uv, 0.0); // 计算六边形的六个顶点 float c = cos(radians(60.0)); float s = sin(radians(60.0)); vec3 p0 = vec3(side, 0.0, 0.0); vec3 p1 = vec3(side * c, -side * s, 0.0); vec3 p2 = vec3(-side * c, -side * s, 0.0); vec3 p3 = vec3(-side, 0.0, 0.0); vec3 p4 = vec3(-side * c, side * s, 0.0); vec3 p5 = vec3(side * c, side * s, 0.0); // 计算当前点是否在六边形内（通过向量叉乘） float r0 = step(0.0, cross(p-p0, p1-p0).z); float r1 = step(0.0, cross(p-p1, p2-p1).z); float r2 = step(0.0, cross(p-p2, p3-p2).z); float r3 = step(0.0, cross(p-p3, p4-p3).z); float r4 = step(0.0, cross(p-p4, p5-p4).z); float r5 = step(0.0, cross(p-p5, p0-p5).z); // 如果在内部，inside = 1.0，否则 inside = 0.0 float inside = r0 * r1 * r2 * r3 * r4 * r5; return vec4(color.rgb, color.a * inside); } void main() { // ... 其他代码 gl_FragColor = drawHex(vec2(0.5, 0.5), 0.5, o); } 参考资料

https://www.bilibili.com/video/BV1X7411F744?p=2

【本文地址】

【分享】Cocos Creator 向量基础及其使用

【分享】Cocos Creator 向量基础及其使用

今日新闻

推荐新闻