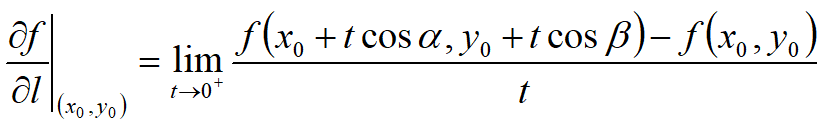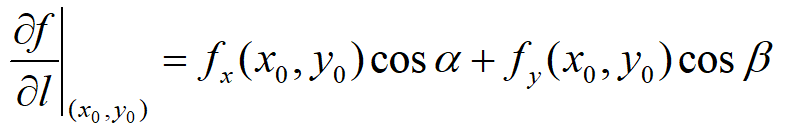方向导数：若u=f(x,y)在点(x0,y0)处可微分，则沿方向el=(cosα,cosβ)的导数为：

其中cos^2(α)+cos^2(β)=1。在函数不存在偏导时，方向导数也可能存在，例如f(x,y)=√(x^2+y^2)在(0,0)处，不存在偏导数，但各方向方向导数存在且为1。当然，假如函数可微，那么必定有方向导数，且可用下式计算。

对于自变量更多的函数，式子类似，都是函数对于该未知量求偏导后，乘以求导方向的单位向量中的对应项

梯度：若函数在D内具有一阶连续偏导数，则对于D内任意一点(x0,y0)，都可确定一个向量

这个向量就叫函数在点(x0,y0)处的梯度，记作grad f(x,y)

某一点方向导数最大值，就是那一点梯度的膜，最小值则为相反数

在求曲面切平面时，把曲面表达式中所有非零的项放到一边，令等式另一边的0变为一个新的因变量，此时新构成的函数的梯度就是切平面的法向量。例：z=x^2-e^(xy)，则新构成的式子为F(x,y,z)=x^2-e^(xy)-z，则定义域内某一点的切平面的法向量为

(2x-y*e^(xy),-x*e^(xy),-1)