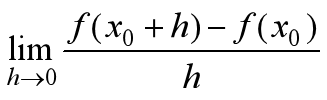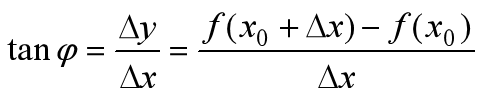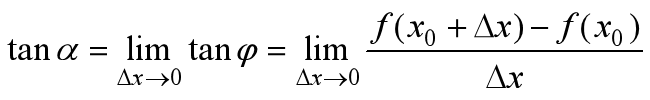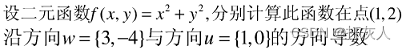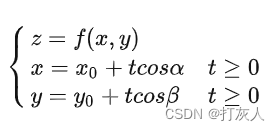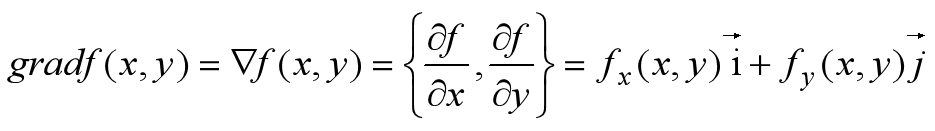数学基础0

您所在的位置：网站首页 › 求导数切线方程过某点 › 数学基础0

数学基础0

2024-01-23 04:12| 来源: 网络整理| 查看: 265

全导数、偏导数、方向导数、梯度都是多元函数(二元及以上)中的概念。本文将从底层介绍全导数、方向导数、偏导数、梯度它们之间的联系和几何意义。

0前言

0.1导数的定义

0.2导数几何意义

1 全导数

1.1 参数方程（过A点任一曲线的参数方程）

1.2 全导数和方向导数、偏导数的关系

1.3 总结

2 方向导数、偏导数和梯度的关系

2.1 方向导数和梯度定义

2.1.1方向导数的定义

2.1.2梯度的定义（梯度和方向导数的关系）

2.2 方向导数和梯度的数学计算

2.2.1方向导数的数学计算

2.2.2梯度的计算

0前言 0.1导数的定义

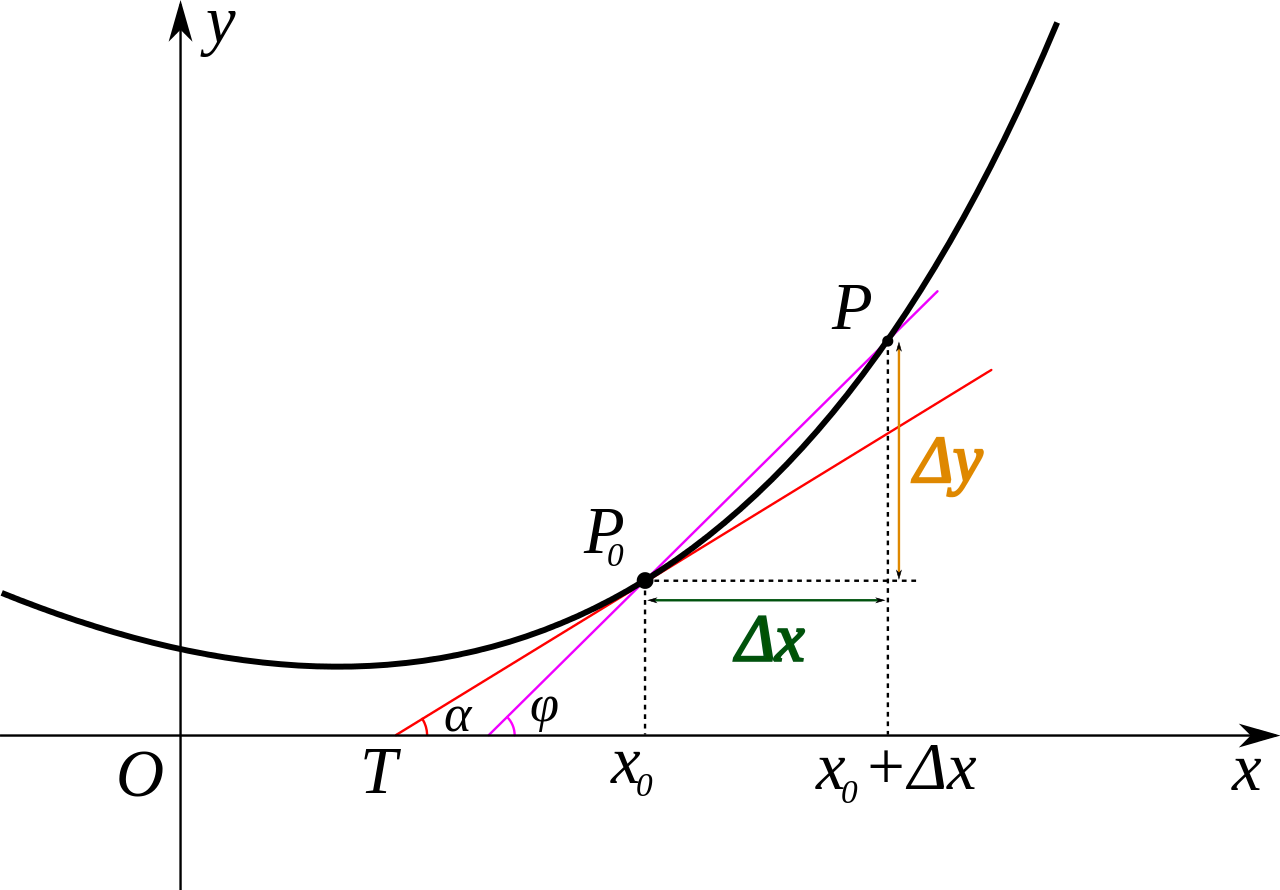
导数（derivative）是微积分学中的一个概念。函数在某一点的导数是指这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。当函数 $f$ 的自变量在一点 $x_{0}$ 上产生一个增量ℎ时，函数输出值的增量与自变量增量ℎ的比值在ℎ趋于0时的极限如果存在，即为 $f$ 在 $x_{0}$ 处的导数，记作 ${f}'(x_{0})$ 、 $\frac{\mathrm{d} f}{\mathrm{d} x}(x_{0})$ 或 $\frac{\mathrm{d} f}{\mathrm{d} x}|_{x=x_{0}}$ 。

0.2导数几何意义

当函数定义域和取值都在实数域中的时候，导数可以表示函数的曲线上的切线斜率。如下图所示，设 $P_{0}$ 为为曲线上的一个定点，P为曲线上的一个动点。当P沿曲线逐渐趋向于 $P_{0}$ 点时并且割线 $PP_{0}$ 的极限位置 $P_{0}T$ 存在,则称 $P_{0}T$ 为曲线在 $P_{0}$ 处的切线。

若曲线为一函数 $y=f(x)$ 的图像，那么割线 $PP_{0}$ （粉红色）的斜率为：

当 $P_{0}$ 处的切线 $P_{0}T$ （橘红色），即 $PP_{0}$ 的极限位置存在时，此时 $\Delta x\rightarrow 0$ ， $\varphi \rightarrow \alpha$ ，则 $P_{0}T$ 的斜率 $tan\alpha$ 为：

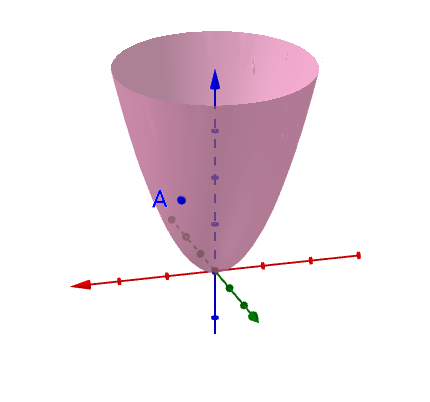
上式与导数定义完全相同，也就是说 $f{}'(x_{0})=tan\alpha$ ，因此，导数的几何意义即曲线 $y=f(x)$ 在点 $P_{0}(x_{0},f(x_{0}))$ 处的切线斜率。

记住1：曲线(函数)在某点的导数=曲线在该点处的斜率

1全导数

step1：下面我用二元函数 $f(x,y)=x^{2}+y^{2}$ 来举例子，选取曲面上的任意一点A ：

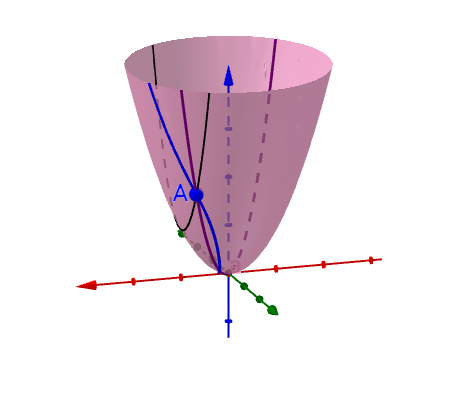
step2：在曲面上可以做无数条过A 点的曲线（图上随便画了三根）：

step3：过A点的每根曲线都可以过A点做各自的切线。比如(随便挑了一根来画)：

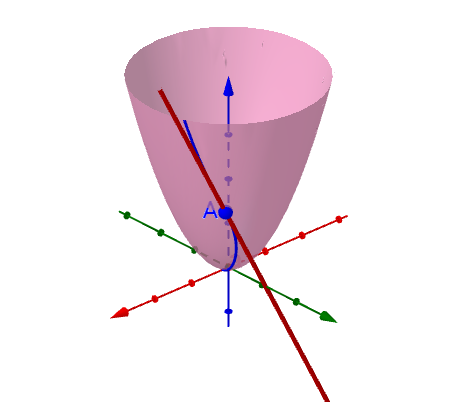
也就是说曲面上任意一点A可对应着无数条曲线，这无数条曲线可过A做无数条切线，即有无数个 “导数值”，我们称之为多元函数上过A点的“全导数”。

1.1参数方程（过A点任一曲线的参数方程）

我们都知道，该曲面的解析式为 $f(x,y)=x^{2}+y^{2}$ ，那么过A点的所有曲线该怎么表示呢？要描述所有这些曲线，我们就需要一些数学手段，这就是参数方程。

我们来看一下，随便画一条过A 点的曲线

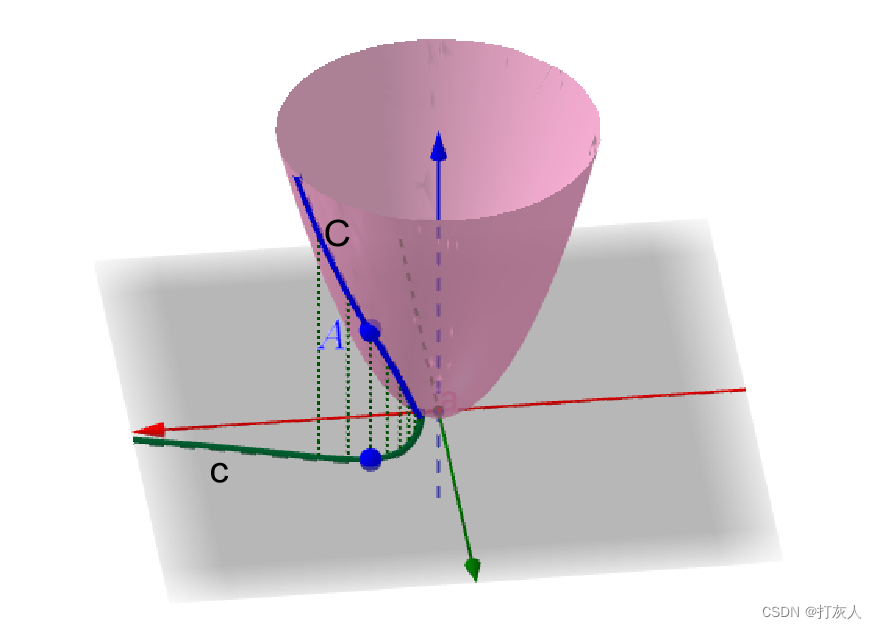
这条曲线也是一个关于x,y的函数f(x,y)，因此它与xy平面上的曲线具有一一对应的关系(如下图)，(我们把函数f(x,y)上的曲线称为曲线C，在xy平面上对应(投影)的曲线称为曲线c)：

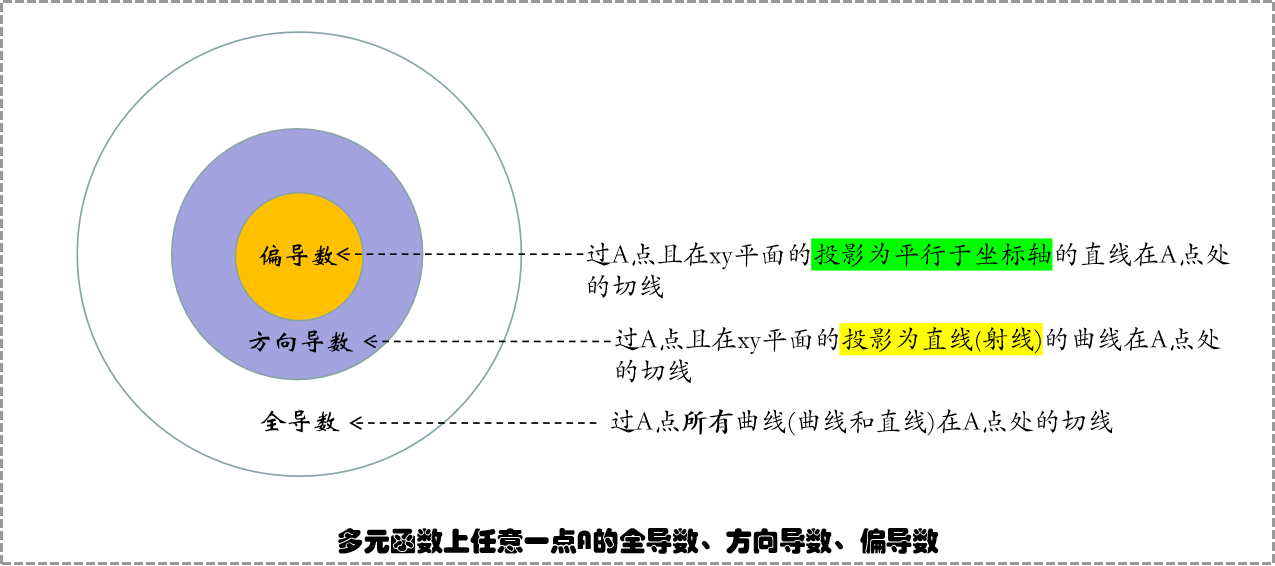
因此我们只需要描述xy面上的曲线c并联立曲面方程 $f(x,y)=x^{2}+y^{2}$ 就可以达到描述曲线C的目的，亦即可得到曲面上过A点任一曲线的参数方程了。（在此不做赘述，详细请看什么是全导数？）

结论：总之，我们暂时知道结论，任意一条曲线，都是通过xy平面上对自变量x，y的限定，来对二元函数 $f(x,y)=x^{2}+y^{2}$ 产生约束得到。(记住2)即任意一条曲线C都可用参数方程来表示。

1.2 全导数和方向导数、偏导数的关系

上面说了，过二元函数中A点的所有曲线C都对应着xy平面中的一条曲线c（广义的，包括曲线和直线），那么在这所有曲线C中也有比较特殊的：曲线c为直线(射线)的曲线C过A点的全导数又被称之为方向导数，而这之中对应直线c平行于坐标轴的曲线C对A点的全导数又被叫做偏导数。

结论:偏导数∈方向导数∈全导数

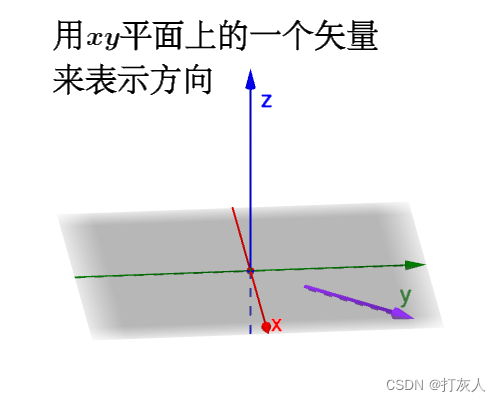
1.3 总结对于多元函数，过函数曲面（以二元f(x,y)为例）上任意一点A可以作出无数条曲线。全导数：每条曲线都有自己过A点的导数，也就是过A点做该曲线的切线。方向导数对应的对象只是无数条曲线中在xy平面上投影为直线(射线)的那部分曲线。方向导数：这部分曲线中的任意一条过A点的导数是方向导数(至于为什么叫方向导数，在下一节中解释)。

我想让大家注意的是：

多元函数的全导数\方向导数\偏导数的求解最终会归结于一条条曲线的求导上，而导数定义和几何意义在前言部分也介绍了（这大家都懂）。每一条曲线都可以用参数方程表示出来，因此完全可以根据定义来求解导数。又因为我们一般研究的对象是方向导数、偏导数它们的参数方程相对来说是简单的（这我在下一节讲），因此我们更不用过于担心它们的求解很难。

2方向导数、偏导数和梯度的关系 2.1 方向导数和梯度定义 2.1.1方向导数的定义

顾名思义，方向导数就是某个方向上的导数。

什么是方向：

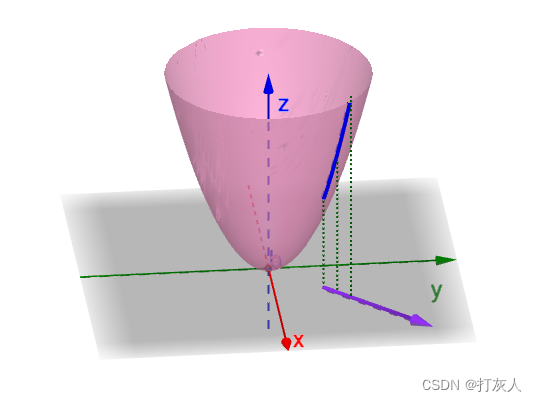
函数 $f(x,y)=x^{2}+y^{2}$ 在这个方向上的图像：

函数f(x,y)的A点在这个方向上也是有切线的，其切线的斜率就是方向导数：

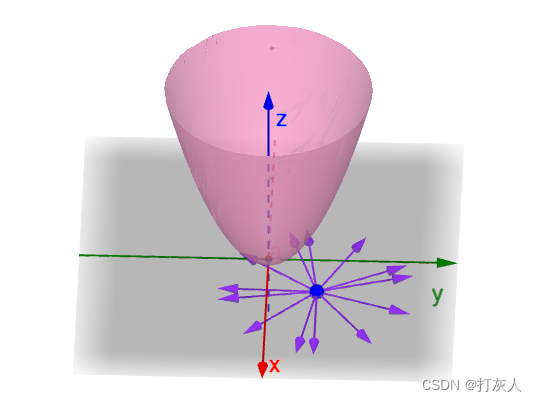
很明显，A点不止一个方向，而是360°都有方向(无数个)：

综上，（1）首先明确方向的定义，xy平面上的一个矢量来表示方向，360°都有方向（注意：方向定义不依赖本案例，优先级是高于本案例的，也就是任何一个多元函数求方向导数都得根据这个方向的定义）。（2）知道了方向的定义，结合第一章对二元函数 $f(x,y)=x^{2}+y^{2}$ 全导数概念的介绍，可知以A点在xy平面上投影点为中心，360°方向的射线对应的所有曲线C为方向导数的研究对象。

方向导数和梯度的几何意义

方向导数本质上是反映函数f(x,y)在一点处的变化率，方向导数最大的方向(变化率最大)所对应的方向为梯度方向，该处的方向导数值为梯度值。但注意，方向导数是标量，梯度是矢量。下面这篇文章一定要仔细的看，读懂读透，对梯度的讲解非常详细。梯度意义:水沿玻璃最“陡”的方向下滑。

2.1.2梯度的定义（梯度和方向导数的关系）

根据方向导数的定义，以A点在xy平面投影点为中心的每个方向对应的曲线C都是有方向导数的。

梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

方向导数最大值的方向取名为梯度方向梯度的值是方向导数的最大值

至于下面问题的答案，请看：如何直观形象地理解方向导数与梯度以及它们之间的关系？

为什么所有方向导数中会存在并且只存在一个最大值？而不是有多个最大值、或者说没有最大值？这个最大值在哪个方向取得？值是多少？ 2.2 方向导数和梯度的数学计算

偏导数、方向导数、梯度之间的关系和数学计算可阅读：

方向导数与梯度https://blog.csdn.net/MyArrow/article/details/51332421

2.2.1方向导数的数学计算

案例：

方向导数曲线对应参数方程：

(cosα，cosβ)是方向w上的单位向量

（1）首先沿w={3，-4}方向的单位向量为 $(\frac{3}{5},-\frac{4}{5})$

则曲线的参数方程为：

（2）有了参数方程，利用导数的定义求解即可

2.2.2梯度的计算

设二元函数 $z=f(x,y)$ 在平面区域D上具有一阶连续偏导数，则对于每一个点P(x,y)都可定出一个向量 $\left \{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right \}=f_{x}(x,y)\vec{i}+f_{y}(x,y)\vec{j}$ ，该函数就称为函数 $z=f(x,y)$ 在P(x,y)的梯度，记作

$grad(x,y)$ 或 $\bigtriangledown f(x,y)$ ,即有：

总结：

方向导数：是一个数（标量）；本质上还是反映的是函数f(x,y)在一点沿某方向v的变化率。偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。梯度：是一个向量：它既有大小（其大小为最大方向导数--每个元素为函数对一元变量的偏导数），也有方向( 梯度的方向是方向导数中取到最大值的方向)

偏导数连续才有梯度存在

参考文献：

导数. 维基百科什么是全导数？马同学，知乎方向导数与梯度_Arrow的博客-CSDN博客_方向导数与梯度公式如何形象地理解方向导数与梯度以及它们之间地关系？知乎

【本文地址】

数学基础0

数学基础0

今日新闻

推荐新闻