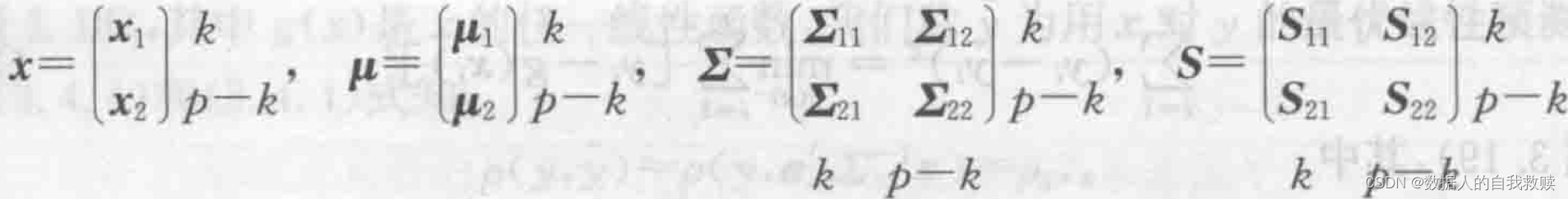|
目录
一、多元正态分布的定义
1.定义
2.二元正态分布
二、多元正态分布的性质
【property1*】
【property2】
【property3】
【property4】
【property5】
【property6】
【property7】
【property8*】
【property9*】
【property10*】
【property11】
三、极大似然估计及估计量的性质
前言
1.极大似然估计
(1)极大似然估计介绍
(2)均值和协差阵的极大似然估计
(3)相关系数的极大似然估计
2.估计量的性质
(1)无偏性
(2)有效性
(3)一致性
(4)充分性
(5)MLE的不变性
四、复相关系数和偏相关系数
1.复相关系数
(1)前言
(2)定义
(3)复相关系数的MLE
2.偏相关系数
(1)前言
(2)引例
(3)定义
(4)一阶偏相关系数
(5)偏相关系数一般递推公式
(6)偏相关系数的MLE
(7)偏协方差矩阵的导出
五、均值和(n-1)S的抽样分布
1.均值的抽样分布
(1)正态总体
(2)非正态总体(多元中心极限定理)
2.(n-1)S的抽样分布
(1)矩阵的拉直
(2)威沙特分布的定义
(3)威沙特分布的性质
(4) (n-1)S的抽样分布
一、多元正态分布的定义
1.定义
一元正态分布 的概率密度函数为: 的概率密度函数为:
![\small f(x)=\frac{1}{\sqrt{2*\pi }\sigma }e^{-\frac{(x-\mu )^2}{2*\sigma ^2}}=(2*\pi )^{-\frac{1}{2}}(\sigma ^2)^{-\frac{1}{2}}exp[-\frac{1}{2}(x-\mu )(\sigma ^2)^{-1}(x-\mu )],-\inftyx+\infty](https://latex.csdn.net/eq?%5Cdpi%7B100%7D%20%5Csmall%20f%28x%29%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B2*%5Cpi%20%7D%5Csigma%20%7De%5E%7B-%5Cfrac%7B%28x-%5Cmu%20%29%5E2%7D%7B2*%5Csigma%20%5E2%7D%7D%3D%282*%5Cpi%20%29%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%28%5Csigma%20%5E2%29%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7Dexp%5B-%5Cfrac%7B1%7D%7B2%7D%28x-%5Cmu%20%29%28%5Csigma%20%5E2%29%5E%7B-1%7D%28x-%5Cmu%20%29%5D%2C-%5Cinfty%3Cx%3C+%5Cinfty)
若随机向量 的概率密度函数为: 的概率密度函数为:
![\small f(x)=(2*\pi)^{-\frac{p}{2}}{\left | \Sigma \right |}^{-\frac{1}{2}}exp[-\frac{1}{2}(x-\mu )^{'}\Sigma ^{-1}(x-\mu )]](https://latex.csdn.net/eq?%5Cdpi%7B100%7D%20%5Csmall%20f%28x%29%3D%282*%5Cpi%29%5E%7B-%5Cfrac%7Bp%7D%7B2%7D%7D%7B%5Cleft%20%7C%20%5CSigma%20%5Cright%20%7C%7D%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7Dexp%5B-%5Cfrac%7B1%7D%7B2%7D%28x-%5Cmu%20%29%5E%7B%27%7D%5CSigma%20%5E%7B-1%7D%28x-%5Cmu%20%29%5D)
则称 服从 服从 元正态分布,记作 元正态分布,记作 ,其中,参数 ,其中,参数 分别为 分别为 的均值和协差阵。 的均值和协差阵。
2.二元正态分布
设 ,这里 ,这里 。易见, 。易见, 是 是 的相关系数。当 的相关系数。当 时,可得 时,可得 的概率密度函数为: 的概率密度函数为:![\small f(x_{1},x_{2})=\frac{1}{2\pi\sigma _{1}\sigma _{2}\sqrt{1-\rho ^2}}exp\left \{ -\frac{1}{2(1-\rho ^2)}[(\frac{x_{1}-\mu_{1}}{\sigma _{1}})^2-2\rho (\frac{x_{1}-\mu_{1}}{\sigma _{1}})(\frac{x_{2}-\mu_{2}}{\sigma _{2}})+(\frac{x_{2}-\mu_{2}}{\sigma _{2}})^2] \right \}](https://latex.csdn.net/eq?%5Cdpi%7B100%7D%20%5Csmall%20f%28x_%7B1%7D%2Cx_%7B2%7D%29%3D%5Cfrac%7B1%7D%7B2%5Cpi%5Csigma%20_%7B1%7D%5Csigma%20_%7B2%7D%5Csqrt%7B1-%5Crho%20%5E2%7D%7Dexp%5Cleft%20%5C%7B%20-%5Cfrac%7B1%7D%7B2%281-%5Crho%20%5E2%29%7D%5B%28%5Cfrac%7Bx_%7B1%7D-%5Cmu_%7B1%7D%7D%7B%5Csigma%20_%7B1%7D%7D%29%5E2-2%5Crho%20%28%5Cfrac%7Bx_%7B1%7D-%5Cmu_%7B1%7D%7D%7B%5Csigma%20_%7B1%7D%7D%29%28%5Cfrac%7Bx_%7B2%7D-%5Cmu_%7B2%7D%7D%7B%5Csigma%20_%7B2%7D%7D%29+%28%5Cfrac%7Bx_%7B2%7D-%5Cmu_%7B2%7D%7D%7B%5Csigma%20_%7B2%7D%7D%29%5E2%5D%20%5Cright%20%5C%7D)
【注】二元正态分布等高线(见课本)
二、多元正态分布的性质
【property1*】
多元正态分布的特征函数为 ,其中 ,其中 。 。
【property2】
设 是一个 是一个 维随机向量,则 维随机向量,则 服从多元正态分布,当且仅当它的任何线性函数 服从多元正态分布,当且仅当它的任何线性函数 ( ( 为 为 维常数向量)均服从一元正态分布 维常数向量)均服从一元正态分布
【property3】
设 ,其中 ,其中 为 为 常数矩阵,则 常数矩阵,则
【注】该性质表明,(多元)正态变量的任何线性变换仍为(多元)正态变量
【eg】设 为 为 维常数向量,则有上述性质2或3可知, 维常数向量,则有上述性质2或3可知,
【eg】设 其中 其中 ,则: ,则:

【property4】
设 ,则 ,则 的任何子向量也服从(多元)正态分布,其均值为 的任何子向量也服从(多元)正态分布,其均值为 的相应子向量,协方差矩阵为 的相应子向量,协方差矩阵为 的相应子矩阵 的相应子矩阵
【注1】该性质表明多元正态分布的任何边缘分布仍为(多元)正态分布
【注2】随机向量的任何边缘分布皆为(多元)正态分布推不出该随机向量服从多元正态分布(反例:习题2.3)
【注3】正态变量的线性组合未必就是正态变量。
 均为一元正态变量 均为一元正态变量 的联合分布为多元正态分布 的联合分布为多元正态分布 的一切线性组合是一元正态变量 的一切线性组合是一元正态变量
【例】设 ,这里 ,这里 ,则: ,则:
   【property5】
【property5】
设 相互独立,且 相互独立,且 ,则对任意 ,则对任意 个常数 个常数 ,有 ,有
【注】此性质表明,独立的多元正态变量(维数相同)的任意线性组合仍为多元正态变量
【property6】
设 ,对 ,对 作如下的剖分: 作如下的剖分: ,其中 ,其中 为 为 矩阵,则子向量 矩阵,则子向量 相互独立,当且仅当 相互独立,当且仅当
【注】可作一般化推广,并对于多元正态变量而言,其子向量之间互不相关和相互独立是等价的
【eg3.2.5】设 ,其中 ,其中 ,则 ,则 不独立, 不独立, 独立 独立
【property7】
设 ,则 ,则
【property8*】
设 ,其中 ,其中 ,则 ,则 相互独立,当且仅当 相互独立,当且仅当 。 。
【property9*】
设 ,其中 ,其中 ,则 ,则 相互独立,当且仅当 相互独立,当且仅当 。 。
【property10*】
设 ,将其作与性质(6)同样的剖分,则 ,将其作与性质(6)同样的剖分,则 相互独立, 相互独立, 也相互独立 也相互独立
【property11】
设 ,对 ,对 作如下的剖分: 作如下的剖分: ,其中 ,其中 为 为 矩阵,则给定 矩阵,则给定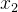 时 时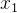 的条件分布为 的条件分布为 ,其中 ,其中 。 。
【注1】 分别成为条件数学期望,条件协方差矩阵。 分别成为条件数学期望,条件协方差矩阵。 通常称为偏协方差矩阵 通常称为偏协方差矩阵
【注2】这一性质可作一般化推广,并对于多元正态变量,其子向量的条件分布仍是(多元)正态
【eg3.2.8】设 ,其中 ,其中 ,试给定 ,试给定 时 时 的条件分布。 的条件分布。


根据【property11】得出![{\color{Blue} \begin{pmatrix} x_{2}-x_{3}\\ x_{1} \end{pmatrix}|x_{1}+2x_{2}\sim N_{2}[\begin{pmatrix} -\frac{2}{5}x_{1}-\frac{4}{5}x_{3}+\frac{4}{5}\\ \frac{1}{2}x_{1}+x_{3}+\frac{5}{2} \end{pmatrix},\begin{pmatrix} \frac{18}{5} &2 \\ 2 & 6 \end{pmatrix}]}](https://latex.csdn.net/eq?%7B%5Ccolor%7BBlue%7D%20%5Cbegin%7Bpmatrix%7D%20x_%7B2%7D-x_%7B3%7D%5C%5C%20x_%7B1%7D%20%5Cend%7Bpmatrix%7D%7Cx_%7B1%7D+2x_%7B2%7D%5Csim%20N_%7B2%7D%5B%5Cbegin%7Bpmatrix%7D%20-%5Cfrac%7B2%7D%7B5%7Dx_%7B1%7D-%5Cfrac%7B4%7D%7B5%7Dx_%7B3%7D+%5Cfrac%7B4%7D%7B5%7D%5C%5C%20%5Cfrac%7B1%7D%7B2%7Dx_%7B1%7D+x_%7B3%7D+%5Cfrac%7B5%7D%7B2%7D%20%5Cend%7Bpmatrix%7D%2C%5Cbegin%7Bpmatrix%7D%20%5Cfrac%7B18%7D%7B5%7D%20%262%20%5C%5C%202%20%26%206%20%5Cend%7Bpmatrix%7D%5D%7D)
三、极大似然估计及估计量的性质
前言
简单随机样本(简称样本):满足 独立,且与总体分布相同。设 独立,且与总体分布相同。设 是从中抽取的一个样本数据矩阵或观测值矩阵: 是从中抽取的一个样本数据矩阵或观测值矩阵: 1.极大似然估计
(1)极大似然估计介绍
似然函数:是样本联合概率密度
1.极大似然估计
(1)极大似然估计介绍
似然函数:是样本联合概率密度 的任意正常数倍,记为 的任意正常数倍,记为 ,将其看作参数 ,将其看作参数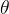 的函数,简记为 的函数,简记为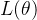 极大似然估计:如果统计量 极大似然估计:如果统计量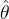 满足 满足 ,则 ,则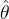 称作 称作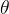 的极大似然估计(MLE)MLE思想:当样本 的极大似然估计(MLE)MLE思想:当样本 给定后,可考虑对不同的 给定后,可考虑对不同的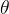 ,联合概率密度如何变,它反映了对样本的解释能力,这便是似然。MLE就是要寻找一个 ,联合概率密度如何变,它反映了对样本的解释能力,这便是似然。MLE就是要寻找一个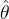 使得这个样本出现的概率最大
(2)均值和协差阵的极大似然估计
一元正态情形: 使得这个样本出现的概率最大
(2)均值和协差阵的极大似然估计
一元正态情形: 多元正态情形: 多元正态情形: ,其中 ,其中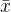 称为样本均值向量, 称为样本均值向量, 称为样本离差矩阵或平方和及叉积和将矩阵, 称为样本离差矩阵或平方和及叉积和将矩阵, 称为样本协方差矩阵
(3)相关系数的极大似然估计 称为样本协方差矩阵
(3)相关系数的极大似然估计

其中 。称 。称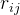 为样本相关系数, 为样本相关系数, 为样本相关矩阵。 为样本相关矩阵。
2.估计量的性质
(1)无偏性
【定义】如果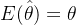 ,则称估计量 ,则称估计量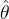 是被估参数 是被估参数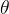 的一个无偏估计,否则就成为有偏的【注1】 的一个无偏估计,否则就成为有偏的【注1】 【注2】 【注2】 是 是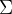 的有偏估计【注3】 的有偏估计【注3】


(2)有效性
【定义】设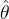 是 是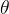 的一个无偏估计,若对 的一个无偏估计,若对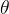 的任一无偏估计 的任一无偏估计 ,有 ,有 ,即 ,即 为非负定矩阵,则称 为非负定矩阵,则称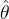 为 为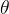 的一致最优无偏估计【注】可以证明,对于多元正态总体, 的一致最优无偏估计【注】可以证明,对于多元正态总体, 分别是 分别是 的一致最优无偏估计
(3)一致性
【定义】如果未知参数 的一致最优无偏估计
(3)一致性
【定义】如果未知参数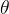 (可以是一个向量或矩阵)的估计量 (可以是一个向量或矩阵)的估计量 随着样本量 随着样本量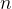 的不断增大,而无限地逼近于真值 的不断增大,而无限地逼近于真值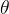 ,则称 ,则称 为 为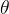 的一致估计(相合估计)【注1】估计量的一致性是在大样本情形下提出的一种要求,而对于小样本,他不能作为评价估计量好坏的准测【注2】可以证明, 的一致估计(相合估计)【注1】估计量的一致性是在大样本情形下提出的一种要求,而对于小样本,他不能作为评价估计量好坏的准测【注2】可以证明, 分别是 分别是 的一致估计(无需总体正态性的假定)
(4)充分性
【定义】如果一个统计量能把含在样本中的有关总体(或有关未知参数)的信息一点都不损失地充分提取出来,则这种统计量就称为充分统计量【注1】可以证明,对于总体 的一致估计(无需总体正态性的假定)
(4)充分性
【定义】如果一个统计量能把含在样本中的有关总体(或有关未知参数)的信息一点都不损失地充分提取出来,则这种统计量就称为充分统计量【注1】可以证明,对于总体 ,当 ,当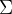 已知时, 已知时,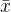 是 是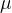 的充分统计量;当 的充分统计量;当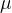 已知时, 已知时, 是 是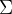 充分统计量【注2】用来作为估计量的充分统计量称为充分估计量。 充分统计量【注2】用来作为估计量的充分统计量称为充分估计量。 这三者之间只相差一个常数倍,所含的信息完全相同,故当 这三者之间只相差一个常数倍,所含的信息完全相同,故当 均未知时, 均未知时, 也都是 也都是 的充分统计量
(5)MLE的不变性
【定义】如果 的充分统计量
(5)MLE的不变性
【定义】如果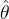 是 是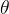 的MLE,那么对于 的MLE,那么对于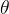 的函数 的函数 ,其MLE是 ,其MLE是 【注】相关系数 【注】相关系数 ,因此其MLE为 ,因此其MLE为 四、复相关系数和偏相关系数
1.复相关系数
(1)前言
(简单)相关系数度量了一个随机变量
四、复相关系数和偏相关系数
1.复相关系数
(1)前言
(简单)相关系数度量了一个随机变量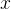 与另一个随机变量 与另一个随机变量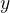 之间线性关系的强弱复相关系数度量了一个随机基变量 之间线性关系的强弱复相关系数度量了一个随机基变量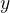 与一组随机变量 与一组随机变量 之间线性关系的强弱
(2)定义 之间线性关系的强弱
(2)定义
设 的相关矩阵 的相关矩阵 。则 。则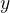 和 和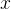 的线性函数 的线性函数 ( (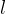 为任一 为任一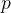 维非零常数向量)间的最大相关系数称为 维非零常数向量)间的最大相关系数称为 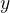 和 和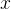 间的复(或多重)相关系数,记作 间的复(或多重)相关系数,记作 ,它度量了一个变量 ,它度量了一个变量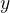 和一组变量 和一组变量 间的相关程度。 间的相关程度。
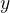 和 和 的相关系数的平方 的相关系数的平方

上述不等式由柯西不等式得到,若取 ,则上述等号成立。所以, ,则上述等号成立。所以, 的复相关系数为: 的复相关系数为:



因而,
【注1】 时,复相关系数退化为简单相关系数的绝对值 时,复相关系数退化为简单相关系数的绝对值
【注2】 的负相关系数为0,当且仅当 的负相关系数为0,当且仅当 不相关(即 不相关(即 ) )
【注3】复相关系数通过 求得,而其中的相关系数对变量单位的改变具有不变性,故复相关系数对变量单位的改变也具有不变性 求得,而其中的相关系数对变量单位的改变具有不变性,故复相关系数对变量单位的改变也具有不变性
【注4】若 互不相关,即 互不相关,即 ,于是有 ,于是有

即此时复相关系数的平方等于 各分量相关系数的平方和 各分量相关系数的平方和
【eg3.4.1】试证随机变量 的任一线性函数 的任一线性函数 与 与 的复相关系数为1 的复相关系数为1


(3)复相关系数的MLE
设样本 的样本相关矩阵 的样本相关矩阵 ,这里 ,这里 则在多元正态的假定下,复相关系数 则在多元正态的假定下,复相关系数 的MLE为: 的MLE为:

称为样本复相关系数。
2.偏相关系数
(1)前言
两个变量之间的相关性,除了受这两个变量彼此间的影响外,常常还受其他一系列变量的影响。由于这个原因,相关系数有时也称为总(或毛,gross)相关系数,其意思是包含了由一切影响带来的相关性。
相关系数有时亦称为简单相关系数或皮尔逊( )相关系数或零阶偏相关系数 )相关系数或零阶偏相关系数
(2)引例
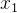 ——家庭的饮食支出, ——家庭的饮食支出,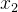 ——家庭的衣着支出, ——家庭的衣着支出,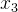 ——家庭的收入 ——家庭的收入
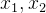 之间存在着较强的正相关性 之间存在着较强的正相关性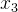 分别与 分别与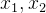 的强正相关性导致了 的强正相关性导致了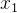 和 和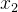 的较强正相关性如果我们能用某种方式把 的较强正相关性如果我们能用某种方式把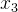 的影响消除掉,或者说控制了 的影响消除掉,或者说控制了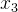 (即 (即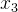 保持不变),则 保持不变),则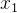 和 和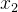 之间(反应净关系)的相关性可能就很不一样了,很有可能会显示负相关性。【注】为了更好地理解本例,我们可设想某地区的这样两个样本:样本1由贫富悬殊的100户家庭组成,其 之间(反应净关系)的相关性可能就很不一样了,很有可能会显示负相关性。【注】为了更好地理解本例,我们可设想某地区的这样两个样本:样本1由贫富悬殊的100户家庭组成,其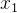 和 和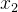 之间一般会有非常强的正相关性;样本2由 之间一般会有非常强的正相关性;样本2由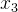 基本相同的100户家庭组成, 基本相同的100户家庭组成, 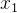 和 和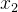 间的相关性一般会比较小或者为负。可以想象,在样本1和样本2中,消除了 间的相关性一般会比较小或者为负。可以想象,在样本1和样本2中,消除了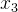 影响后的 影响后的 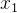 和 和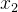 之间的相关性一般会比较接近,且样本2中的 之间的相关性一般会比较接近,且样本2中的 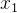 和 和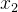 间的相关性往往不太受 间的相关性往往不太受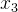 的影响
(3)定义 的影响
(3)定义
将 剖分如下: 剖分如下:
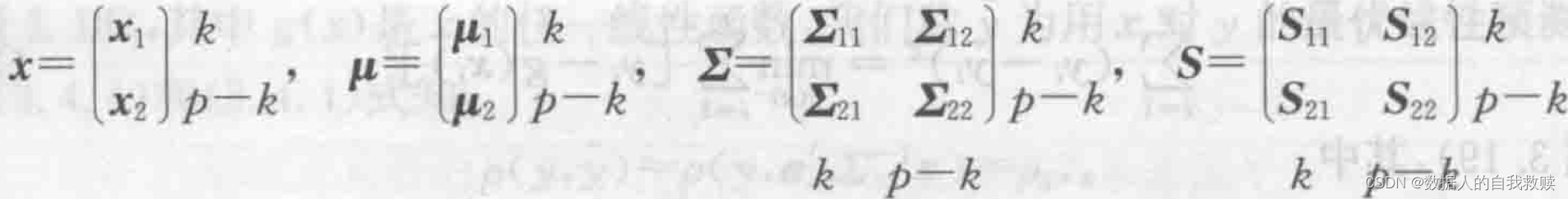
称 为给定 为给定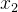 时 时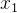 的偏协方差矩阵。记 的偏协方差矩阵。记 ,称 ,称 为偏协方差,它是剔除了 为偏协方差,它是剔除了 的(线性)影响之后, 的(线性)影响之后,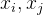 之间的协方差。 之间的协方差。
给定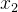 时 时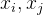 的偏相关系数定义为 的偏相关系数定义为

【注1】 度量了剔除 度量了剔除 的(线性)影响后, 的(线性)影响后,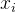 和 和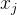 间相关关系的强弱【注2】对于多元正态变量,由于 间相关关系的强弱【注2】对于多元正态变量,由于 也是条件协方差矩阵,故此时偏相关系数与条件相关系数是同一个值,从而 也是条件协方差矩阵,故此时偏相关系数与条件相关系数是同一个值,从而 同时也度量了在 同时也度量了在 给定的条件下 给定的条件下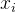 和 和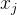 间相关关系的强弱【注3】当 间相关关系的强弱【注3】当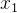 和 和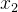 不相关(即 不相关(即 时), 时), ,从而 ,从而 (4)一阶偏相关系数
(4)一阶偏相关系数
可直接由相关系数算得,设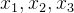 是三个随机变量,则有: 是三个随机变量,则有:



【注1】 并不意味着 并不意味着 ,反之亦然 ,反之亦然
【注2】 未必同号,且大小无必然规律 未必同号,且大小无必然规律
(5)偏相关系数一般递推公式

(6)偏相关系数的MLE
在多元正态性的假设下, 的MLE为: 的MLE为:

其中, ,称 ,称 为样本偏相关系数。 为样本偏相关系数。
(7)偏协方差矩阵的导出

五、均值和(n-1)S的抽样分布
1.均值的抽样分布
(1)正态总体
设 是从总体 是从总体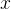 中抽取的一个样本,则 中抽取的一个样本,则
(2)非正态总体(多元中心极限定理)
设 是来自总体 是来自总体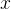 的一个样本, 的一个样本, 存在,则当 存在,则当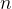 很大且 很大且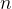 相对于 相对于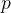 也很大时, 也很大时, 近似服从 近似服从 。 。
2.(n-1)S的抽样分布
(1)矩阵的拉直
设随机矩阵 ,将 ,将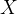 的列向量一个接一个组成一个长向量,记作 的列向量一个接一个组成一个长向量,记作 ,即 ,即 ,称“vec”为拉直运算。当 ,称“vec”为拉直运算。当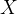 是 是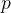 阶对称矩阵时,因 阶对称矩阵时,因 ,故只需取其下三角部分组成一个缩减了的常向量,记作 ,故只需取其下三角部分组成一个缩减了的常向量,记作 ,即 ,即

随机矩阵X的分布是指 或(当 或(当 时) 时) 的分布,拉直运算将矩阵分布问题转化为了向量分布问题。 的分布,拉直运算将矩阵分布问题转化为了向量分布问题。
(2)威沙特分布的定义
设随机向量 独立同分布于 独立同分布于 ,则 ,则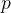 阶矩阵 阶矩阵 的分布称为自由度为 的分布称为自由度为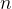 的( 的(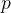 阶)威沙特 阶)威沙特 分布,记作 分布,记作 。 。
当 时,显然有 时,显然有 ,即有 ,即有 。 。
因此,威沙特 分布是卡方分布在多元场合下的一种推广。 分布是卡方分布在多元场合下的一种推广。
(3)威沙特分布的性质
设 且相互独立,则 且相互独立,则 设 设 , ,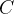 为 为 常数矩阵,则 常数矩阵,则 (4) (n-1)S的抽样分布
(4) (n-1)S的抽样分布
设 是取自 是取自 的一个样本, 的一个样本, ,则可以证明 ,则可以证明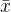 和 和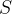 相互独立,且有 相互独立,且有 。 。
|