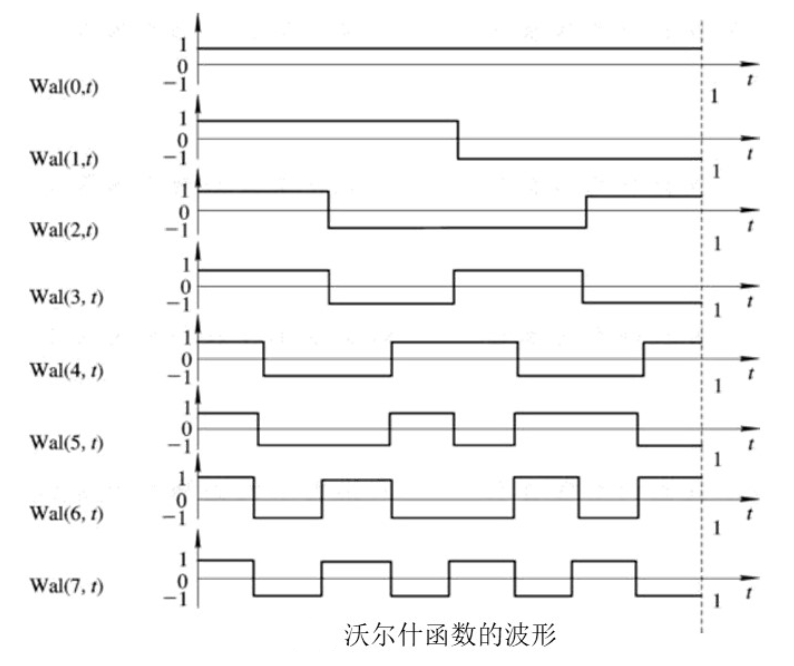
本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。

若两个周期为 T 的模拟信号 s 1 ( t ) s_{1}(t) s1​(t) 和 s 2 ( t ) s_{2}(t) s2​(t) 互相正交, 则有 ∫ 0 T s 1 ( t ) s 2 ( t ) d t = 0 \int_{0}^{T} s_{1}(t) s_{2}(t) d t=0 ∫0T​s1​(t)s2​(t)dt=0 同理, 若 M 个周期为 T 的模拟信号 s 1 ( t ) s_{1}(t) s1​(t), s 2 ( t ) s_{2}(t) s2​(t), … \ldots …, s M ( t ) s_{M}(t) sM​(t) 构成一个正交信号集合，则有 ∫ 0 T s i ( t ) s j ( t ) d t = 0 i ≠ j ; i , j = 1 , 2 , … , M \int_{0}^{T} s_{i}(t) s_{j}(t) d t=0 \quad i \neq j ; \quad i, j=1,2, \ldots, M ∫0T​si​(t)sj​(t)dt=0i=j;i,j=1,2,…,M

对于二进制数字信号, 用一数字序列表示码组。这里, 我们只讨论二进制且码长相同的编码。这时, 两个码组的正交性可用如下形式的互相 关系数来表述。

设长为 n \boldsymbol{n} n 的编码中码元只取值 +1 和 -1 , 假设 x \boldsymbol{x} x 和 y \boldsymbol{y} y 是其中两个码组: x = ( x 1 , x 2 , x 3 , ⋯   , x n ) y = ( y 1 , y 2 , y 3 , ⋯   , y n ) x=(x_{1}, x_{2}, x_{3}, \cdots, x_{n}) \quad y=(y_{1}, y_{2}, y_{3}, \cdots, y_{n}) x=(x1​,x2​,x3​,⋯,xn​)y=(y1​,y2​,y3​,⋯,yn​) 其中: x i , y i ∈ ( + 1 , − 1 ) , i = 1 , 2 , ⋯   , n x_{i}, y_{i} \in(+1,-1), \quad i=1,2, \cdots, n xi​,yi​∈(+1,−1),i=1,2,⋯,n

若码组 x 和 y 正交, 则必有 ρ ( x , y ) = 0 \rho(x, y)=0 ρ(x,y)=0 。 ρ ( x , y ) = 1 n ∑ i = 1 n x i y i \rho(x, y)=\frac{1}{n} \sum_{i=1}^{n} x_{i} y_{i} ρ(x,y)=n1​i=1∑n​xi​yi​

例如, 右图所示 4 个数字信号可以看作是如下4 个码组:

{ s 1 ( t ) : ( + 1 , + 1 , + 1 , + 1 ) s 2 ( t ) : ( + 1 , + 1 , − 1 , − 1 ) s 3 ( t ) : ( + 1 , − 1 , − 1 , + 1 ) s 4 ( t ) : ( + 1 , − 1 , + 1 , − 1 ) . \{\begin{array}{l} s_{1}(t):(+1,+1,+1,+1) \\ s_{2}(t):(+1,+1,-1,-1) \\ s_{3}(t):(+1,-1,-1,+1) \\ s_{4}(t):(+1,-1,+1,-1) \end{array}. {s1​(t):(+1,+1,+1,+1)s2​(t):(+1,+1,−1,−1)s3​(t):(+1,−1,−1,+1)s4​(t):(+1,−1,+1,−1)​.

按照互相关系数定义式计算容易得知, 这 4 个码组中任意两者之间的相关系数都为 0 , 即这 4 个码组两两正交。我们把这种两两正交的编码称为正交编码。

用二进制数字表示互相关系数

在二进制编码理论中, 常采用二进 制数字 “ 0 ”和 “ 1 ”表示码元的可能 取值。这时, 若规定用二进制数字 “0”代替上述码组中的 “+ 1 ”, 用 二进制数字 “ 1 ”代替 “ -1 ”, 则上 述互相关系数定义式将变为 ρ ( x , y ) = A − D A + D \rho(x, y)=\frac{A-D}{A+D} ρ(x,y)=A+DA−D​ 式中, A——x 和 y 中对应码元相同的个数;

D—— x 和 y 中对应码元不同的个数。

例如, 按照左式规定, 上面例 子可以改写成

{ s 1 ( t ) : ( 0 , 0 , 0 , 0 ) s 2 ( t ) : ( 0 , 0 , 1 , 1 ) s 3 ( t ) : ( 0 , 1 , 1 , 0 ) s 4 ( t ) : ( 0 , 1 , 0 , 1 ) . \{\begin{array}{l} s_{1}(t):(0,0,0,0) \\ s_{2}(t):(0,0,1,1) \\ s_{3}(t):(0,1,1,0) \\ s_{4}(t):(0,1,0,1) \end{array}. {s1​(t):(0,0,0,0)s2​(t):(0,0,1,1)s3​(t):(0,1,1,0)s4​(t):(0,1,0,1)​.

可以验证互相关系数 ρ = 0 \boldsymbol{\rho}=\mathbf{0} ρ=0 .

上式中, 若用 x 的 j 次循环移位代替 y , 就得到 x 的自相关系数 ρ x ( j ) \rho_{x}(j) ρx​(j) 。 具体地讲，令 x = ( x 1 , x 2 , ⋯   , x n ) y = ( x 1 + j , x 2 + j , ⋯   , x n , x 1 , x 2 , ⋯ x j ) \begin{array}{l} x=(x_{1}, x_{2}, \cdots, x_{n}) \\ y=(x_{1+j}, x_{2+j}, \cdots, x_{n}, x_{1}, x_{2}, \cdots x_{j}) \end{array} x=(x1​,x2​,⋯,xn​)y=(x1+j​,x2+j​,⋯,xn​,x1​,x2​,⋯xj​)​ 代入定义式 ρ ( x , y ) = A − D A + D \rho(x, y)=\frac{A-D}{A+D} ρ(x,y)=A+DA−D​

就得到自相关系数 ρ x ( j ) \rho_{x}(j) ρx​(j) : ρ x ( j ) = ( A − D ) / n \rho_{x}(j)=(A-D) / n ρx​(j)=(A−D)/n 类似上述互相关系数的定义, 可以对于一个长为 n 的码组 x 定义其自相关系数为 ρ x ( j ) = 1 n ∑ i = 1 n x i x i + j , j = 0 , 1 , ⋯   , ( n − 1 ) \rho_{x}(j)=\frac{1}{n} \sum_{i=1}^{n} x_{i} x_{i+j}, \quad j=0,1, \cdots,(n-1) ρx​(j)=n1​i=1∑n​xi​xi+j​,j=0,1,⋯,(n−1) 式中, x 的下标按模 n 运算, 即有 x n + k ≡ x k x_{n+k} \equiv \mathbf{x}_{k} xn+k​≡xk​ 。例如, 设

x = ( x 1 , x 2 , x 3 , x 4 ) = ( + 1 , − 1 , − 1 , + 1 ) x=(x_{1}, x_{2}, x_{3}, x_{4})=(+1,-1,-1,+1) x=(x1​,x2​,x3​,x4​)=(+1,−1,−1,+1) 则有 ρ x ( 0 ) = 1 4 ∑ i = 1 4 x i 2 = 1 ρ x ( 1 ) = 1 4 ∑ i = 1 4 ‾ ‾ 4 x i x i + 1 = 1 4 ( x 1 x 2 + x 2 x 3 + x 3 x 4 + x 4 x 1 ) = 1 4 ( − 1 + 1 − 1 + 1 ) = 0 ρ x ( 2 ) = 1 4 ∑ i = 1 1 x i x i + 2 = 1 4 ( x 1 x 3 + x 2 x 4 + x 3 x 1 + x 4 x 2 ) = − 1 ρ x ( 3 ) = 1 4 ∑ i = 1 4 ‾ 1 x i x i + 3 = 1 4 ( x 1 x 4 + x 2 x 1 + x 3 x 2 + x 4 x 3 ) = 0 \begin{array}{l} \rho_{x}(0)=\frac{1}{4} \sum_{i=1}^{4} x_{i}^{2}=1\\ \rho_{x}(1)=\frac{1}{4} \sum_{i=1}^{\overline{\overline{4}}^{4}} x_{i} x_{i+1}=\frac{1}{4}(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{4}+x_{4} x_{1})=\frac{1}{4}(-1+1-1+1)=0 \\ \rho_{x}(2)=\frac{1}{4} \sum_{i=1}^{1} x_{i} x_{i+2}=\frac{1}{4}(x_{1} x_{3}+x_{2} x_{4}+x_{3} x_{1}+x_{4} x_{2})=-1 \\ \rho_{x}(3)=\frac{1}{4} \sum_{i=1}^{\overline{4}^{1}} x_{i} x_{i+3}=\frac{1}{4}(x_{1} x_{4}+x_{2} x_{1}+x_{3} x_{2}+x_{4} x_{3})=0 \end{array} ρx​(0)=41​∑i=14​xi2​=1ρx​(1)=41​∑i=144​xi​xi+1​=41​(x1​x2​+x2​x3​+x3​x4​+x4​x1​)=41​(−1+1−1+1)=0ρx​(2)=41​∑i=11​xi​xi+2​=41​(x1​x3​+x2​x4​+x3​x1​+x4​x2​)=−1ρx​(3)=41​∑i=141​xi​xi+3​=41​(x1​x4​+x2​x1​+x3​x2​+x4​x3​)=0​

超正交码：相关系数 ρ \rho ρ 的取值范围在 ± 1 \pm 1 ±1 之间, 即有 $ -1 \leq \rho \leq+1$ 。 若两个码组间的相关系数 ρ < 0 \rhos1​(t):(0,0,0,0)s2​(t):(0,0,1,1)s3​(t):(0,1,1,0)s4​(t):(0,1,0,1)​

其反码为

{ ( 1 , 1 , 1 , 1 ) ( 1 , 1 , 0 , 0 ) ( 1 , 0 , 0 , 1 ) ( 1 , 0 , 1 , 0 ) \{\begin{array}{l}(1,1,1,1) \\ (1,1,0,0) \\ (1,0,0,1) \\ (1,0,1,0)\end{array} {(1,1,1,1)(1,1,0,0)(1,0,0,1)(1,0,1,0)​

上两者的总体即构成如下双正交码:

( 0 , 0 , 0 , 0 ) ( 1 , 1 , 1 , 1 ) ( 0 , 0 , 1 , 1 ) ( 1 , 1 , 0 , 0 ) ( 0 , 1 , 1 , 0 ) ( 1 , 0 , 0 , 1 ) ( 0 , 1 , 0 , 1 ) ( 1 , 0 , 1 , 0 ) (0,0,0,0) \quad(1,1,1,1) \quad(0,0,1,1) \quad(1,1,0,0)(0,1,1,0) \quad(1,0,0,1) \quad(0,1,0,1) \quad(1,0,1,0) (0,0,0,0)(1,1,1,1)(0,0,1,1)(1,1,0,0)(0,1,1,0)(1,0,0,1)(0,1,0,1)(1,0,1,0)

此码共有 8 种码组, 码长为 4 。

沃尔什(Walsh)函数集是完备的非正弦型的二元（取值为+1与-1）正交函数集, 其相应的离散沃尔什函数简称为沃尔什序列或沃尔什码。 沃尔什函数是定义在半开区间 [0,1) 的矩形波族, 每个矩形波有一个编号 n( n = 0 , 1 , 2 , 3 , … n=0,1,2,3, \ldots n=0,1,2,3,…) 。

矩形波幅度的取值为 +1 或 -1 , 规定起始时矩形波的取值为 +1 , 然后在 +1 与 -1 之间变化, 变化的次数 (+1 变 -1 与 -1 变 +1 的次数之和） m = n m=n m=n , 在 +1 或 -1 上持续的时间可以相等, 也可以不相等 (不相等时较长的持续时间 T 1 T_{1} T1​ 为较短的持续时间 T s T_{\mathrm{s}} Ts​ 的两倍）。 编号为 n 的沃尔什函数用 W a l ( n , t ) \mathrm{Wal}(n, t) Wal(n,t) 表示, 沃尔什函数的波形如图所示。

补充（度量空间）的完备性定义:

度量空间 X = ( X , d ) X=(X, d) X=(X,d) 中的序列 ( x n ) (x_{n}) (xn​) , 如果对任意给定的 $ \varepsilon \gt 0 $, 都存在一个 N = N ( ε ) \mathrm{N}=\mathrm{N}(\varepsilon) N=N(ε) , 使得对每个 m \mathrm{m} m, n > N \mathrm{n}>\mathrm{N} n>N 都有 d ( x m , x n ) < ε \mathrm{d}(\mathrm{x}_{\mathrm{m}}, \mathrm{x}_{\mathrm{n}})1,0,​i=ji=j​i,j=0,1,2,⋯.

该性质为沃尔什函数基本性质中最重要的性质。

(2) 除 W a l ( 0 , t ) \mathrm{Wal}(0, t) Wal(0,t) 外，其他 W a l ( n , t ) \mathrm{Wal}(n, t) Wal(n,t) 在半开区间 [0,1) 上的均值为 0 .

(3) 两个沃尔什函数相乘仍为沃尔什函数，即 Wal ⁡ ( i , t ) Wal ⁡ ( j , t ) = Wal ⁡ ( k t ) \operatorname{Wal}(i, t) \operatorname{Wal}(j, t)=\operatorname{Wal}(kt) Wal(i,t)Wal(j,t)=Wal(kt) 这表示沃尔什函数对于乘法是自闭的。

(4) 沃尔什函数集是完备的, 即长度为 N \mathrm{N} N 的离散沃尔什函数 (沃尔什序列)一共有 N \mathrm{N} N 个。

(5) 沃尔什函数在同步时是完全正交的。

(6) 沃尔什函数在不同步时, 其自相关和互相关特性均不理想, 并随同步误差值的增大而快速恶化。

(7) 同长度不同编号的walsh函数的频带宽度不同。

参考文献：