原标题：欧几里得空间、希尔伯特空间、赋范空间等空间的概念与辨析

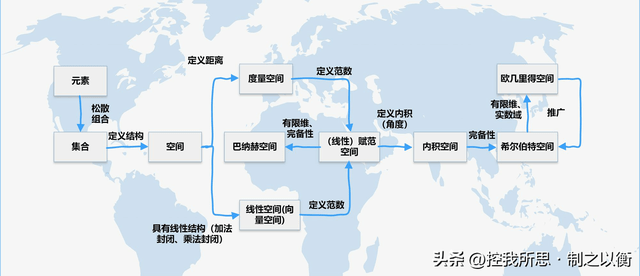
1. 空间：元素组合在一起构成集合，对这些组合在一起的元素定义它们相互之间的某种“结构/关系”后就成为了“空间”。

2. 度量空间：如果元素之间“结构/关系”是用“距离”描述的，则称度量空间。“距离”的定义满足如下要求：

- 非负性：

- 非退化性：

- 对称性：

- 三角不等式：

3. 线性空间（向量空间）：

- 在空间中定义加法(+)运算和乘法(×)运算

- 加法(+)封闭：对于任意的, 且唯一

- 乘法(×)封闭：对于任意的, 且唯一（是一个空间）

- 加法(+)运算和乘法(×)运算如果满足加法结合律、加法交换律、加法的零元、加法的逆元、数乘的结合律、数乘的单位元、分配律则称为线性空间

4. （线性）赋范空间：定义范数的空间为赋范空间，由于范数是定义在线性空间上的，所以赋范空间一定是线性的，有时可简称为赋范空间。

- 范数需满足

- 非负性：

- 非退化性：

- 齐次性：

- 三角不等式：

5. 内积空间：定义与角度相关的”结构/关系“——内积（Inner product）又称标量积（Scalar product）、点积（Dot product）

- 内积定义为，内积满足如下四个条件：

- 共轭对称性：

- 第一变元的线性性：

- 第二变元共轭线性：

- 非负性：

- 内积空间具有基于空间本身的内积所自然定义的范数，所以内积空间一定是赋范空间，进而也属于度量空间、线性空间

6. 希尔伯特（Hilbert）空间：内积空间+完备性

- 完备性：距离空间中的柯西列是否都收敛

- 柯西列：设为度量空间，取度量空间上的序列，当对任意的，存在，当时满足时，称为柯西列

- 收敛：设为度量空间，为中的数列，若存在使得，则在中收敛,，称为收敛列，称为的极限，记做 。

- 例如在空间中，数列是一个柯西列，但不收敛。由该例可知，一个完备的度量空间一定是一个闭集

7. 巴纳赫（Banach）空间：完备的（线性）赋范空间

8. 欧几里得（Euclidean）空间：将希尔伯特空间限制在实数域和有限维，同时希尔伯特空间时欧几里得空间的推广。返回搜狐，查看更多

责任编辑：