概率论与数理统计基础概念与重要定义汇总 |
您所在的位置:网站首页 › 概率概念的发展过程 › 概率论与数理统计基础概念与重要定义汇总 |
概率论与数理统计基础概念与重要定义汇总
|
文章目录
一、随机事件和概率1:互斥,对立,独立事件的定义和性质。2:概率,条件概率和五大概率公式3:古典型,几何型概率和伯努利试验4:易错问题汇总
二、随机变量及其分布1:随机变量及其分布函数2:常用分布
三、多维随机变量及其分布1-二维随机变量及其分布2-随机变量的独立性3-两个随机变量
Z
=
g
(
X
,
Y
)
Z=g(X,Y)
Z=g(X,Y)的分布
四、随机变量的数字特征1:随机变量的数学期望2:随机变量的方差3:常用随机变量的数学期望和方差4:矩、协方差和相关系数
五、理解大数定律和中心极限定律1:大数定律和中心极限定理的区别和联系2:简单总结他们的作用
六、参数估计1:点估计2:矩估计3:最大似然估计
一、随机事件和概率
1:互斥,对立,独立事件的定义和性质。
互斥事件 \color{red}\textbf{互斥事件} 互斥事件 事件A和B的交集为空,A与B就是互斥事件,也叫互不相容事件。也可叙述为:不可能同时发生的事件。如A∩B为不可能事件(A∩B=Φ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中不会同时发生。 则P(A+B)=P(A)+P(B)(这个公式何时成立在我一面thu叉院的时候被问到过,我神tm就答了一个相互独立/(ㄒoㄒ)/~~)且P(A)+P(B)≤1 对立事件 \color{red}\textbf{对立事件} 对立事件 若A交B为不可能事件,A并B为必然事件,那么称A事件与事件B互为对立事件,其含义是:事件A和事件B必有一个且仅有一个发生。 对立事件概率之间的关系:P(A)+P(B)=1。例如,在掷骰子试验中,A={出现的点数为偶数},b={出现的点数为奇数},A∩B为不可能事件,A∪B为必然事件,所以A与B互为对立事件。 互斥事件与对立事件两者的联系在于:对立事件属于一种特殊的互斥事件。 它们的区别可以通过定义看出来:一个事件本身与其对立事件的并集等于总的样本空间;而若两个事件互为互斥事件,表明一者发生则另一者必然不发生,但不强调它们的并集是整个样本空间。即对立必然互斥,互斥不一定会对立。 独立事件 \color{red}\textbf{独立事件} 独立事件 设A,B是试验E的两个事件,若 P ( A ) > 0 P(A)>0 P(A)>0,可以定义 P ( B ∣ A ) P(B∣A) P(B∣A).一般A的发生对B发生的概率是有影响的,所以条件概率 P ( B ∣ A ) ≠ P ( B ) P(B∣A)≠P(B) P(B∣A)=P(B),而只有当A的发生对B发生的概率没有影响的时候(即A与B相互独立)才有条件概率 P ( B ∣ A ) = P ( B ) P(B∣A)=P(B) P(B∣A)=P(B).这时,由乘法定理 P ( A ∩ B ) = P ( B ∣ A ) P ( A ) = P ( A ) P ( B ) . P(A∩B)=P(B∣A)P(A)=P(A)P(B). P(A∩B)=P(B∣A)P(A)=P(A)P(B). 定义:设A,B是两事件,如果满足等式 P ( A ∩ B ) = P ( A B ) = P ( A ) P ( B ) P(A∩B)=P(AB)=P(A)P(B) P(A∩B)=P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立. 容易推广:设A,B,C是三个事件,如果满足 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B), P ( B C ) = P ( B ) P ( C ) P(BC)=P(B)P(C) P(BC)=P(B)P(C), P ( A C ) = P ( A ) P ( C ) P(AC)=P(A)P(C) P(AC)=P(A)P(C), P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC)=P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C),则称事件A,B,C相互独立 更一般的定义是, A 1 , A 2 , … … , A n A1,A2,……,An A1,A2,……,An是 n ( n ≥ 2 ) n(n≥2) n(n≥2)个事件,如果对于其中任意2个,任意3个,…任意n个事件的积事件的概率,都等于各个事件概率之积,则称事件 A 1 , A 2 , … , A n A1,A2,…,An A1,A2,…,An相互独立 2:概率,条件概率和五大概率公式概率公理与条件概率 \color{red}\textbf{概率公理与条件概率} 概率公理与条件概率 什么是概率?设实验E的样本空间为 Ω \Omega Ω,则称实值函数 P P P为概率,如果 P P P满足下列三个条件 对于任意事件A,满足 P ( A ) ≥ 0 P(A)\geq0 P(A)≥0对于必然事件 Ω \Omega Ω有 P ( A ) = 1 P(A)=1 P(A)=1对于两两互斥的可数无穷个事件 A 1 , A 2 , . . . , A N . . . A_1,A_2,...,A_N... A1,A2,...,AN...,有 P ( A 1 ∪ A 2 ∪ . . . ∪ A N ∪ . . . ) = P ( A 1 ) + P ( A 2 ) + . . . + P ( A N ) + . . . P(A_1\cup A_2\cup...\cup A_N\cup...)=P(A_1)+P(A_2)+...+P(A_N)+... P(A1∪A2∪...∪AN∪...)=P(A1)+P(A2)+...+P(AN)+...什么是条件概率?设 A , B A,B A,B为两个事件,且 P ( A ) > 0 P(A)>0 P(A)>0,称 P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB) 为在事件A发生的条件下事件B发生的条件概率。 五大概率公式 \color{red}\textbf{五大概率公式} 五大概率公式 加法公式: P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(A\cup B)=P(A)+P(B)-P(AB) P(A∪B)=P(A)+P(B)−P(AB),P(A∪B∪C)=P(A)+P(B)+P©-P(AB)-P(BC)-P(AC)+P(ABC).减法公式: P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB)乘法公式:当 P ( A ) > 0 P(A)>0 P(A)>0时, P ( A B ) = P ( A ) P ( B ∣ A ) P(AB)=P(A)P(B|A) P(AB)=P(A)P(B∣A)全概率公式:设 B 1 , B 2 , . . . , B n B_1,B_2,...,B_n B1,B2,...,Bn为样本区间内概率均不为零的一个完备事件组,则对任意事件 A A A,有 P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)=\sum_{i=1}^n P(B_i)P(A|B_i) P(A)=∑i=1nP(Bi)P(A∣Bi)。贝叶斯公式:设 B 1 , B 2 , . . . , B n B_1,B_2,...,B_n B1,B2,...,Bn为样本区间内概率均不为零的一个完备事件组,则对任意事件 A A A且 P ( A ) > 0 P(A)>0 P(A)>0,有 P ( B j ∣ A ) = P ( B j ) P ( A ) P ( A ) = P ( B j ) P ( A ∣ B j ) ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(B_j|A)=\frac{P(B_j)P(A)}{P(A)}=\frac{P(B_j)P(A|B_j)}{\sum_{i=1}^nP(B_i)P(A|B_i)} P(Bj∣A)=P(A)P(Bj)P(A)=∑i=1nP(Bi)P(A∣Bi)P(Bj)P(A∣Bj) 3:古典型,几何型概率和伯努利试验
古典型-能通过样本点数出来的概率
\color{red}\textbf{古典型-能通过样本点数出来的概率}
古典型-能通过样本点数出来的概率
几何型:通过几何度量计算的概率
\color{red}\textbf{几何型:通过几何度量计算的概率}
几何型:通过几何度量计算的概率 伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。单个伯努利试验是没有多大意义的,然而,当我们反复进行伯努利试验,去观察这些试验有多少是成功的,多少是失败的,事情就变得有意义了,这些累计记录包含了很多潜在的非常有用的信息。 4:易错问题汇总 P ( A ∪ B ) = 1 P(A\cup B)=1 P(A∪B)=1不能推出 A ∪ B = Ω A\cup B=\Omega A∪B=Ω,同样 P ( A B ) = 0 P(AB)=0 P(AB)=0也不能推出 A B = ∅ AB=\emptyset AB=∅。这两个关系只能从右往左推,仅给出概率是得不到事件的结论的。 二、随机变量及其分布 1:随机变量及其分布函数随机变量 \color{red}\textbf{随机变量} 随机变量 在样本空间 Ω \Omega Ω上的实值函数 X = X ( ω ) , ω ∈ Ω X=X(\omega),\omega\in\Omega X=X(ω),ω∈Ω称为随机变量,简记为 X X X。随机变量不是一个变量,而是实值函数。 分布函数 \color{red}\textbf{分布函数} 分布函数 分布函数(英文Cumulative Distribution Function, 简称CDF),是概率统计中重要的函数,正是通过它,可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征,分布函数可以完整地描述随机变量的统计规律,并且决定随机变量的一切其他概率特征。 分布函数 F ( x ) F(x) F(x)是定义在 ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)上的一个实值函数, F ( x ) F(x) F(x)的值等于随机变量 X X X在区间 ( − ∞ , x ] (-\infty,x] (−∞,x]上取值的概率,即事件 X ≤ x X\leq x X≤x的概率: F ( x ) = P ( X ≤ x ) , x ∈ ( − ∞ , ∞ ) \color{blue}F(x)=P(X\leq x),x\in (-\infty,\infty) F(x)=P(X≤x),x∈(−∞,∞) 分布函数的性质主要有三条,单调不减,负无穷收敛到0 lim x → + ∞ F ( x ) = 1 \lim_{x\rightarrow+\infty} F(x)=1 limx→+∞F(x)=1,正无穷收敛到1。右连续性 F ( x + 0 ) = F ( x ) F(x+0)=F(x) F(x+0)=F(x). 这三个条件同样是 F ( x ) F(x) F(x)成为某一随机变量的分布函数的充分必要条件。 分布函数的定义对于离散型随机变量和连续型随机变量都是一致的,但是对于连续型随机变量而言,他还有概率密度 把随机变量的概率分布表推广到无限情况,就可以得到连续型随机变量的概率密度函数。 此时,随机变量取每个具体的值的概率为0,但在落在每一点处的概率是有相对大小的,描述这个概念的,就是概率密度函数。 你可以把这个想象成一个实心物体,在每一点处质量为0,但是有密度,即有相对质量大小,他有以下两条主要的性质。 伯努利分布(0-1分布) \color{red}\textbf{伯努利分布(0-1分布)} 伯努利分布(0-1分布) 0 — 1 0—1 0—1分布就是 n = 1 n=1 n=1情况下的二项分布。即只先进行一次事件试验,该事件发生的概率为 p p p,不发生的概率为 1 − p 1-p 1−p。这是一个最简单的分布,任何一个只有两种结果的随机现象都服从 0 − 1 0-1 0−1分布。 二项分布 \color{red}\textbf{二项分布} 二项分布 一般地,如果随机变量
X
X
X有分布律 含义:在
n
n
n次独立重复的伯努利试验中,若每次实验的成功率为
p
p
p,则在
n
n
n次独立重复实验种成功的总次数
X
X
X服从二项分布。当
n
=
1
n=1
n=1时,二项分布退化为
0
−
1
0-1
0−1分布。
几何分布
\color{red}\textbf{几何分布}
几何分布 如果随机变量
X
X
X的分布律为: 含义:在
n
n
n次伯努利试验中,试验
k
k
k次才得到第一次成功的机率服从几何分布
超几何分布
\color{red}\textbf{超几何分布}
超几何分布 如果随机变量
X
X
X的分布律为: 含义:如果 N N N件产品中含有 M M M件次品,从中任意一次取出 n n n件(不放回依次取出 n n n件),另 X X X=抽取的 n n n件产品中的次品件数,则 X X X服从参数为 n , N , M n,N,M n,N,M的超几何分布。 如果有放回的取 n n n次,那么服从 B ( N , M N ) B(N,\frac{M}{N}) B(N,NM)。
泊松分布
\color{red}\textbf{泊松分布}
泊松分布 如果随机变量
X
X
X的分布律为: 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。 在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率
λ
λ
λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布
P
(
λ
)
P(λ)
P(λ)。
指数分布
\color{red}\textbf{指数分布}
指数分布 连续型均匀分布:如果连续型随机变量
X
X
X具有如下的概率密度函数,
正态分布
\color{red}\textbf{正态分布}
正态分布 如果随机变量
X
X
X的概率密度为: 二维随机变量 \color{red}\textbf{二维随机变量} 二维随机变量 设 X = X ( = ω ) X=X(=\omega) X=X(=ω), Y = Y ( ω ) Y=Y(\omega) Y=Y(ω)是定义在样本空间 Ω \Omega Ω上的两个随机变量,则称向量 ( X , Y ) (X,Y) (X,Y)为二维随机变量或者随机向量。 二维随机变量的分布 \color{red}\textbf{二维随机变量的分布} 二维随机变量的分布 F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(X\leq x,Y\leq y) F(x,y)=P(X≤x,Y≤y),该分布具有如下的性质 对任意的 x , y x,y x,y, 0 ≤ F ( x , y ) ≤ 1 0\leq F(x,y)\leq 1 0≤F(x,y)≤1 F ( − ∞ , y ) = F ( x , − ∞ ) = F ( − ∞ , − ∞ ) = 0 , F ( + ∞ , + ∞ ) = 1 F(-\infty,y)=F(x,-\infty)=F(-\infty,-\infty)=0,F(+\infty,+\infty)=1 F(−∞,y)=F(x,−∞)=F(−∞,−∞)=0,F(+∞,+∞)=1 F ( x , y ) F(x,y) F(x,y)关于 x , y x,y x,y均单调不减而且右连续。 P ( a < X ≤ b , c < Y ≤ d ) = F ( b , d ) − F ( b , c ) − F ( a , d ) + F ( a , c ) P(a |
【本文地址】
今日新闻 |
推荐新闻 |

 伯努利试验:独立重复实验
\color{red}\textbf{伯努利试验:独立重复实验}
伯努利试验:独立重复实验
伯努利试验:独立重复实验
\color{red}\textbf{伯努利试验:独立重复实验}
伯努利试验:独立重复实验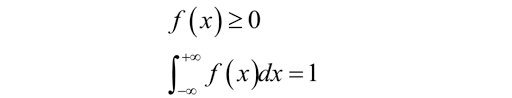
 则称
X
X
X服从参数为
n
n
n和
p
p
p的二项分布,我们记为
X
∼
B
(
n
,
p
)
X\thicksim B(n,p)
X∼B(n,p)或
X
∼
b
(
n
,
p
)
X\thicksim b(n,p)
X∼b(n,p)。
则称
X
X
X服从参数为
n
n
n和
p
p
p的二项分布,我们记为
X
∼
B
(
n
,
p
)
X\thicksim B(n,p)
X∼B(n,p)或
X
∼
b
(
n
,
p
)
X\thicksim b(n,p)
X∼b(n,p)。 则称
X
X
X服从参数为
p
p
p的几何分布。
则称
X
X
X服从参数为
p
p
p的几何分布。 则称
X
X
X服从参数为
n
,
N
,
M
n,N,M
n,N,M的超几何分布。
则称
X
X
X服从参数为
n
,
N
,
M
n,N,M
n,N,M的超几何分布。 则称
X
X
X服从参数为
λ
\lambda
λ的泊松分布,记为
X
∼
P
(
λ
)
X\thicksim P(\lambda)
X∼P(λ)。
则称
X
X
X服从参数为
λ
\lambda
λ的泊松分布,记为
X
∼
P
(
λ
)
X\thicksim P(\lambda)
X∼P(λ)。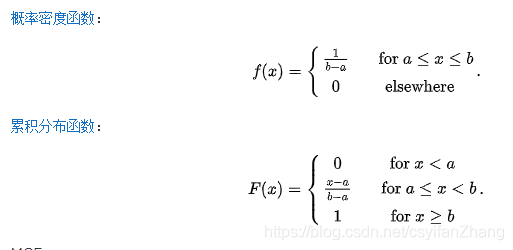 则称
X
X
X服从
[
a
,
b
]
[a,b]
[a,b]上的均匀分布(uniform distribution),记为
X
∼
U
(
a
,
b
)
X\thicksim U(a,b)
X∼U(a,b)。
则称
X
X
X服从
[
a
,
b
]
[a,b]
[a,b]上的均匀分布(uniform distribution),记为
X
∼
U
(
a
,
b
)
X\thicksim U(a,b)
X∼U(a,b)。 其中
μ
,
σ
\mu,\sigma
μ,σ为常数而且
σ
>
0
\sigma>0
σ>0,则称
X
X
X服从参数为
μ
,
σ
\mu,\sigma
μ,σ的正态分布,记作
X
∼
N
(
μ
,
σ
2
)
X\thicksim N(\mu,\sigma^2)
X∼N(μ,σ2)。当
μ
=
0
,
σ
2
=
1
\mu=0,\sigma^2=1
μ=0,σ2=1时,称
X
X
X服从标准正态分布。
其中
μ
,
σ
\mu,\sigma
μ,σ为常数而且
σ
>
0
\sigma>0
σ>0,则称
X
X
X服从参数为
μ
,
σ
\mu,\sigma
μ,σ的正态分布,记作
X
∼
N
(
μ
,
σ
2
)
X\thicksim N(\mu,\sigma^2)
X∼N(μ,σ2)。当
μ
=
0
,
σ
2
=
1
\mu=0,\sigma^2=1
μ=0,σ2=1时,称
X
X
X服从标准正态分布。