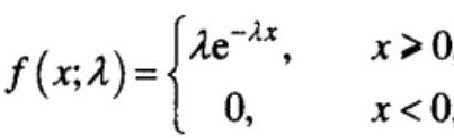【概率】常见分布（离散/连续）、卷积公式（实际意义与作用、公式、记忆法）

您所在的位置：网站首页 › 概率密度函数xy › 【概率】常见分布（离散/连续）、卷积公式（实际意义与作用、公式、记忆法）

【概率】常见分布（离散/连续）、卷积公式（实际意义与作用、公式、记忆法）

2023-11-15 15:33| 来源: 网络整理| 查看: 265

发现自己对各种分布不太熟悉，决定趁此机会整理一下，看有没有比较好的记忆方法。

各种分布最重要的理解它的实际意义，都是解决什么问题的，其次是公式的含义。

所以下面都按以下几点来展开：实际意义、数学表达、对表达式的解释。

一、离散型变量的分布

1. 0—1分布（两点分布）X~B(1,p)

2. 二项分布（n重伯努利分布）X~B(n,p)

3. 泊松分布 X~P(λ)

4. 几何分布 X~G(p)

二、连续型变量的分布

1. 均匀分布 X~U(a, b)

2. 指数分布

三、卷积公式

一、离散型变量的分布 1. 0—1分布（两点分布）X~B(1,p)

只进行一次事件试验，该事件发生的概率为p，不发生的概率为1-p。任何一个只有两种结果的随机事件都服从0-1分布。是n=1时的二项分布。

，k=0，1。k=0时，表示某随机事件失败的概率；k=1，表示某随机事件成功的概率。

分布律（下表）。E(X)=p；D(X)=p(1-p)。

X01P(x)1-pp 2. 二项分布（n重伯努利分布）X~B(n,p)

重复n次独立的伯努利实验（伯努利试验是在同样条件下重复、独立进行的一种随机试验，其特点是只有两种可能结果：发生或者不发生）。单个伯努利试验没有多大意义，反复进行时可以观察成功次数，此时的分析更有意义。

【例】某售货员电话推销n次中，成功k次的概率。

$P(X=k)= C_{n}^{k}p^k(1-p)^{n-k}$ ，k=0，1，……n。在n次实验中成功次数为k时的概率。

E(X)=np；D(X)=np(1-p)。

记忆：二项分布就是n重伯努利分布，二项“伯”。

《二项分布（Binomial Distribution）》：https://blog.csdn.net/huangjx36/article/details/77990392

3. 泊松分布 X~P(λ)

描述单位时间内随机事件发生的次数。参数λ——单位时间(或单位面积)内随机事件的平均发生次数。

【例】某网站平均每分钟有2次访问，下一分钟内的访问量是λ的概率。

表示某单位时间内，随机事件发生k次的概率。

E(X)=D(X)=λ。

记忆：一天内停车场没“泊”几辆车，太轻“松”，是因为λ、e两个人都有帽子（都有指数）。

4. 几何分布 X~G(p)

在n次伯努利试验中，第k次才首次成功的概率。是前k-1次都失败，第k次成功的概率。

【例】某产品的不合格率为0.05，则首次查到不合格品时的检查次数X ～ G(0.05) 。

记忆：首次成功做出几何题。

二、连续型变量的分布 1. 均匀分布 X~U(a, b)

表示区间 [a, b] 内任意等长度区间内事件出现的概率相同的分布。

【例】在一小时内，分针某时刻的角度值满足均匀分布，可研究该角度在40°~80°内的概率。

2. 指数分布

表示两次相继发生的随机事件的时间/空间间隔的概率。参数λ——单位时间(或单位面积)内随机事件的平均发生次数。

【例】电子元件的寿命为多少的概率；接电话的等待时间。

，

（对期望的理解：如果平均每小时接到2个电话，则接一个电话的平均预期等待时间是半个小时。）

《泊松分布和指数分布：10分钟教程》：http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html

《二项分布、指数分布与泊松分布的关系》：https://blog.csdn.net/u013164612/article/details/82596583

《泊松分布 & 指数分布》：https://www.cnblogs.com/think-and-do/p/6483335.html

三、卷积公式 1. 实际意义与作用

每年都向一个垃圾填埋场填埋垃圾，垃圾中有毒物质会被逐渐降解，求最终某天填埋场中有毒物质的残余量则是卷积。

每年连续存钱（存钱函数）情况下，经过复利（复利函数）作用，最终得到的钱。

一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

一个持续的输入信号与自身延迟的部分的叠加。

信号函数，在系统对信号的响应（响应函数）下，得到的结果（输出）是过去产生的所有信号经过系统的处理（响应）后得到的结果的叠加。

“卷”是因为输入信号、输出信号坐标轴上下放置时，t=0的输入信号在输出的t=10处，而输入t=10的在输出的t=0处，所以需要翻转然后平移，相乘，求积。

卷积应用常被称作滤波，卷积核被称为滤波器。因为卷积可以平滑图像，如在研究服装款式时，可以去除商标、颜色等，即过滤图像中除了边缘外的所有信息，只保留衣服轮廓。卷积核不同，可以达到锐化或模糊图像的效果。

《卷积神经网络-基础》：https://mlnotebook.github.io/post/CNN1/

写的很详细，推荐。

2. 公式（数学三范围）

设（X，Y）是二维连续型随机变量，具有概率密度 f(x, y)，则 Z=X+Y 为连续型随机变量，且概率密度为

$f_{X+Y}(z)=\int_{-\infty }^{+\infty }f(z-y,y)dy\overset{X,Y ind}{\rightarrow}\int_{-\infty }^{+\infty }f_{X}(z-y)f_{Y}(y)dy$

$f_{X+Y}(z)=\int_{-\infty }^{+\infty }f(x,z-x)dx\overset{X,Yind}{\rightarrow} \int_{-\infty }^{+\infty }f_{X}(x)f_{Y}(z-x)dx$

(ind是indenpendent的简写，表示条件 “X,Y独立”。)

2.1 推导

具体推导过程从 F 定义式入手，将二重积分拆成二次积分，然后求导得 f 是一次积分。（这里的x+y≤z不是下限，应该写在下面，表示在该区域和定义域的交集处做积分！）

$F_{Z}(z)=P\left \{ Z\leqslant z \right \}=\iint_{x+y\leqslant z}f(x,y)dxdy$

注：这一思路也点出了卷积公式的作用。

即对于求两个连续型随机变量复合函数的密度函数，诸如 Z=X+Y，Z=Y/X，Z=XY 形式。

方法[1]是从分布函数定义出发，对满足 Z≤z 区域的 f(x, y) 积分，再求导得密度函数。方法[2]是用卷积函数，直接用一次积分求出密度函数。 2.2 推广

求Z=Y/X，Z=XY的分布函数时，均可用类似的方法。如下。

相关链接：《利用推广的卷积公式解决二维连续型随机变量函数的分布》：https://kaoyan.wendu.com/shuxue/fuxi/115018.shtml

里面有对于定义法和卷积法求的具体例题，可参考。

3. 记忆

以对 dx 积分为例，卷积函数及推广式可统一定义为下式。观察发现，积分限是-∞到+∞；积分函数是两部分的乘积，一部分是密度函数，对 dx 积分，就不能出现 y，所以要把 y 换成 x、z 表达式 y=h(x,z)，另一部分是表达式 y=h(x,z) 对 z 的偏导数的绝对值，这里是求偏导，也即认为 x 是常数。所以，对谁积分，就把其他变量换掉，再乘上换掉的变量表达式对 z 的偏导的绝对值。

$f_{Z}(z)=\int_{-\infty }^{+\infty }f(x,h(x,z))\cdot \left | \frac{\partial h(x,z)}{\partial z} \right |dx$

（内容过零碎，没有小结。）

【本文地址】

【概率】常见分布（离散/连续）、卷积公式（实际意义与作用、公式、记忆法）

【概率】常见分布（离散/连续）、卷积公式（实际意义与作用、公式、记忆法）

今日新闻

推荐新闻