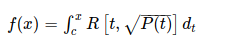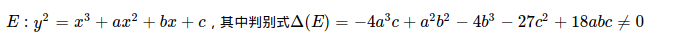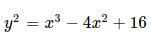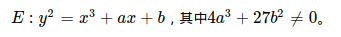椭圆曲线加密算法依赖于椭圆曲线理论，后者理论涵盖的知识比较深广，而且涉及数论中比较深奥的问题。经过数学家几百年的研究积累，已经有很多重要的成果，一些很棘手的数学难题依赖椭圆曲线理论得以解决（比如费马大定理）。

本文涉及的椭圆曲线知识只是抽取与密码学相关的很小的一个角落，涉及到很浅的理论的知识，同时也是一点比较肤浅的总结和认识，重点是利用椭圆曲线结合数学技巧阐述加密算法的过程和原理。

本文特意构造有比较多的实例方便理解其过程和原理。

椭圆曲线方程来源于椭圆积分，后者来最初来源于计算椭圆周长的问题，有一段时间的历史了，在欧拉时期就开始研究。椭圆周长没有精确的初等函数的公式表示，只有近似的公式表示，精确的椭圆周长可以用不定积分表示。

现在一般将形如如下形式的积分定义为椭圆积分：

 其中R是其两个参数的有理函数，P是一个无重根的3或4阶多项式，而c是一个常数。椭圆曲线方程与P(t)表现形式比较相像。

数学上的椭圆曲线一般由如下形式给出：

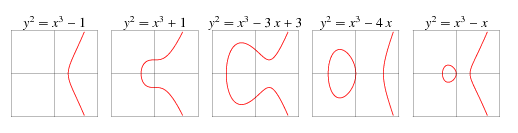
 椭圆曲线都是关于X轴对称的曲线。

典型的椭圆曲线如：

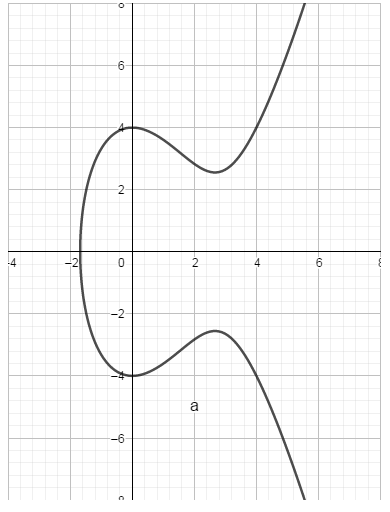
 ，其图像为：

更多的椭圆曲线图像：

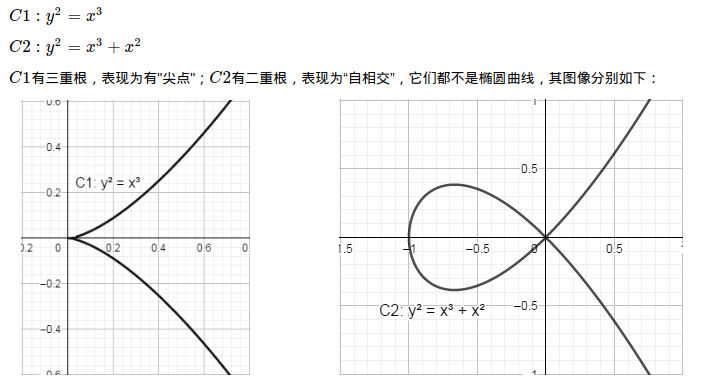
 限定Δ不为零有特殊的意义。如果判别式Δ(E)等于零，由三次方程判别式判定理可知，方程x3+ax2+bx+c=0存在二重根或者三重根，曲线表现为"自相交"或者有“尖点”。

两个典型的例子是:

在密码学中用到的椭圆曲线方程一般限定为：

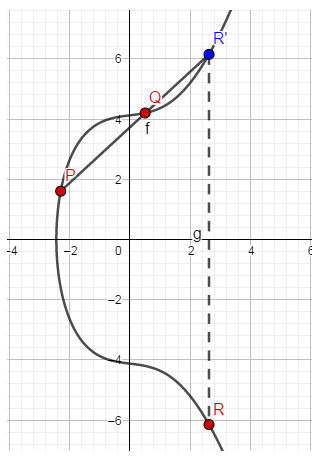
 也即是这里的二次项系数为0。

椭圆曲线上可以定义一些很有意思的特殊运算规则。一般来说会定义两种运算：加法和数乘运算。

加法运算是点与点之间的运算；数乘运算基于加法运算，重复的加法运算就是数乘。

已知椭圆曲线上两个不同的点P和Q，则这两个点之和R=P+Q可以通过如下操作得到：过P、Q两点做直线L，与椭圆曲线相交于第三点，该点关于X轴的对称点即是所求的R点。椭圆曲线的这种加法运算有比较明确的几何含义。如下所示：

 以这种比较奇特的规则来定义加法运算会让人觉得比较怪异，其思想很可能是借鉴于求椭圆曲线有理解的方法（没有去严格考据）。

求椭圆曲线有理解考虑的问题是寻找有理点(x,y)使其满足椭圆曲线方程。其求解过程是在有限的已知有理点的集合中，选两个点P1,P2，作直线与椭圆曲线相交与第三点个有理点Q3。此时如果再利用P1,P2,Q3三个点中的任意两点作直线不能在产生新的有理解（因为他们本身是已经在一条直线上，不会产生新的交点），但是考虑Q3关于X轴对称的点Q′3必定也是有理点，于是可以利用Q3′与P1或者Q3′与P2继续做直线与椭圆曲线相交得到新的有理解，对新的交点再取对称点，以此迭代下去。由此利用交点的对称点作直线来生成新的交点，进而可逐步求解满足椭圆曲线的有理解。

椭圆曲线加法运算的规则中“取交点的对称点”正是与上述求解过程及其相似。

对于加法运算也有另外一种描述：若椭圆曲线上三个点在同一直线上，则他们的和为O，也即是P+Q+R′=O，其中的O是无穷远点或者零点。

更完整的椭圆曲线加法运算规则如下：

1、O+O=O，对任意的P，有P+O=P；O看做零点，对加法运算没有实际贡献（类似于四则运算加法运算中的0）。

2、P=(x,y)的负元是关于X中对称的点−P=(x,−y)（而不是关于原点对称），P+(−P)=O。过P和−P的直线与X轴垂直，实际上可以看做它与椭圆曲线相交于无穷远点（射影平面，也即是在欧式平面上添加了无穷远点和无穷远直线的平面），因此将也将O视作无穷远点。

3、计算P和Q的和是通过做过P和Q两点的直线，与椭圆曲线相交于第三点，再取该点关于X轴的对称点以此作为P,Q之和，正如上面的几何图形展示的那样。

4、计算P点（P≠O）的两倍时，是做该点的切线，再取交点S关于X轴的对称点−S，也即是2P=P+P=−S容易验证，对于椭圆曲线上的点和O点组成的集合，以及集合上定义的二元加法运算，构成一个Abel群。单位元是O点，P(x,y)的逆元是P(x,−y)，封闭性，结合性以及交换性也是显然满足的。

1.2、加法运算的代数解释

几何解释更直观，代数解释更有利于数值计算。

过曲线上P(xp,yp)和Q(xQ,yQ)两点（P和Q不互为负元）做直线，求与曲线的第三个交点的问题是很容易用代数的方法来描述的。

也即是求：

{y2=x3+ax+by−yp=k(x−xp)(1)(2)其中斜率k=yQ−yPxQ−xP。

将（2）代入（1）再利用次数对齐的方式容易求得第三个交点的对称点也即P,Q之和R(xR,yR)为：

xR=k2−xP−xQyR=−yP+k(xP−xR)如果需要计算倍乘，可以让多个点自身重复相加得到。例如P+P=2P=R，当yP≠0时，代数描述为：

xR=(3x2P+a2yP)2−2xP

yR=(3x2P+a2yP)(xP−xR)−yP2、模素数P的加法运算

密码学中普遍采用的是有限域上的椭圆曲线，也即是变元和系数均在有限域中取值的椭圆曲线。使用模素数p的有限域Zp，将模运算引入到椭圆曲线算术中，变量和系数从集合0,1,2,...,p−1中取值而非是在实数上取值。

此时讨论椭圆曲线形式如下：

y2modp=(x3+ax+b)modp其中(4a3+27b2)modp≠0modp，变量和系数均在Zp中取值。

将满足上式的所有非负整数对和O点记为集合Ep(a,b)，这是一个有限的离散点集。由此可知集合中的点分布在(0,0)到(p−1,p−1)的象限中，集合中的点有可能刚好也在椭圆曲线上，更多的可能是在椭圆曲线外。例如点(13,7)是满足y2mod23=(x3+x+1)mod23的点，但是(13,7)并不在椭圆曲线上。

实际上，集合Ep(a,b)与模p的加法运算构成循环阿贝尔群，其生成元，阶和生成子群问题在本节后面会讨论。

对于较小的素数p，完全可以暴力穷举找出集合Ep(a,b)中的点。比如参数a=1,b=3,p=23，E23(1,3)有27个点（包含O点），暴力穷举这些点分别为（第八节给出了一些分析椭圆曲线问题的demo实现）：

复制代码(0,7) (6,15) (15,9)(0,16) (7,10) (15,14)(2,6) (7,13) (19,2)(2,17) (10,1) (19,21)(4,5) (10,22) (21,4)(4,18) (12,8) (21,19)(5,8) (12,15) (22,1)(5,15) (14,1) (22,22)(6,8) (14,22) O复制代码Ep(a,b)上的加法规则和实数域上的加法基本一致，只是多加了模运算。但是模p的加法没有显而易见的几何解释，只有代数描述。

求解(xR,yR)的代数表达式为：

xR=(λ2−xP−xQ)modpyR=(λ(xP−xR)−yP)modp其中

λ=⎧⎩⎨⎪⎪(yQ−yPxQ−xP)modp(3x2P+a2yP)modp(P≠Q)(P=Q)例如a=1,b=1,p=23,P(3,10),Q(13,16)，求R=P+Q.

此时P≠Q，计算λ=(yQ−yPxQ−xP)modp=(16−1013−3)mod23=6×10−1mod23.

要计算上式首先要计算10−1mod23.

令x≡10−1(mod23)，由于10≡10(mod23)，所以10x≡1(mod23)，利用扩展欧几里德算法求得x=7.

λ=6×7mod23=19所以

xR=(λ2−xP−xQ)modp=(192−3−13)mod23=345mod23=0yR=(λ(xP−xR)−yP)modp=(19×(3−0)−10)mod23=47mod23=1所以R=(0,1).

还可以按照以上规则计算2P,3P等等倍乘点。

实际上E23(1,1)中共有28个点（包含无穷远点O），以P(3,10)开始的所有倍乘点：P,2P,3P...27P,28P可以暴力计算得出:

复制代码P=(3,10)2P=(7,12)3P=(19,5)4P=(17,3)5P=(9,16)6P=(12,4)7P=(11,3)8P=(13,16)9P=(0,1)10P=(6,4)11P=(18,20)12P=(5,4)13P=(1,7)14P=(4,0)15P=(1,16)16P=(5,19)17P=(18,3)18P=(6,19)19P=(0,22)20P=(13,7)21P=(11,20)22P=(12,19)23P=(9,7)24P=(17,20)25P=(19,18)26P=(7,11)27P=(3,13)28P=O复制代码容易验证，上述计算过程中Q(13,16)点就是8P，P+Q=P+8P=9P=(0,1)，与上述计算结果是吻合的，读者也可以验证更多的结果。

现在提出一个问题：Ep(a,b)中有多少个点呢？这个问题的准确答案并不好回答，但是有一些粗略的规律。

设Ep(a,b)中点的个数为Np，并且ap=p−Np，实际上Np与p比较接近。

Hasse定理表明：

|ap|