|
目录
1. 样条函数定义
2. 样条曲线简介
3. 样条插值法
4. 三次样条曲线
1. 样条函数定义
样条是一种特殊的函数,由多项式分段定义。在插值问题中,样条插值通常比多项式插值好用。用低阶的样条插值能产生和高阶的多项式插值类似的效果,并且可以避免被称为龙格现象(Runge phenonmenon) 的数值不稳定的出现,并且低阶的样条插值还具有“保凸”的重要性质。
备注:在计算方法中,有利用多项式对某一函数的近似逼近,计算相应的函数值。一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越准确。插值次数越高,插值结果越偏离原函数的现象称为龙格现象。
样条函数的优点:与多项式拟合比较,样条函数可以保证穿过所有点,样条函数是多项式的分段函数,同时保证点之间平滑过渡,一阶导数/二阶导数
2. 样条曲线简介
样条曲线Spline本质是分段多项式实函数,在实数范围内有:![S:[a,b]\rightarrow \Re](https://private.codecogs.com/gif.latex?S%3A%5Ba%2Cb%5D%5Crightarrow%20%5CRe) ,在区间 ,在区间![[a,b]](https://private.codecogs.com/gif.latex?%5Ba%2Cb%5D) 上包含 上包含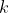 个子区间 个子区间![[t_{i-1},t_{i}]](https://private.codecogs.com/gif.latex?%5Bt_%7Bi-1%7D%2Ct_%7Bi%7D%5D) ,且有: ,且有:
 (1) (1)
对应每一段区间 i 的存在多项式:![P_{i}:[t_{i-1},t_{i}]\rightarrow \mathbb{R}](https://private.codecogs.com/gif.latex?P_%7Bi%7D%3A%5Bt_%7Bi-1%7D%2Ct_%7Bi%7D%5D%5Crightarrow%20%5Cmathbb%7BR%7D) ,且满足于: ,且满足于:

 (2) (2)
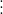

其中, 多项式中最高次项的幂,视为样条的阶数或次数(Order of spline)。 根据子区间 多项式中最高次项的幂,视为样条的阶数或次数(Order of spline)。 根据子区间![[t_{i-1},t_{i}]](https://private.codecogs.com/gif.latex?%5Bt_%7Bi-1%7D%2Ct_%7Bi%7D%5D) 的区间长度是否一致分为均匀(Uniform)样条和非均匀(Non_uniform)样条。 的区间长度是否一致分为均匀(Uniform)样条和非均匀(Non_uniform)样条。
满足了公式(2)的多项式有很多,为了保证曲线在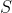 区间内具有足够的平滑度,一条 区间内具有足够的平滑度,一条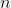 次样条,同时应具备处处连续且可微的性质: 次样条,同时应具备处处连续且可微的性质:
 (3) (3)
其中,
3. 样条插值法
样条插值:一种以可变样条来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的,每一个多项式都是由相邻的两个数据点决定的,这样,任意的两个相邻的多项式以及它们的导数在连接点处都是连续的。(简单理解就是每两个点之间确定一个函数,这个函数就是一个样条,函数不同,样条就不同,所以定义中说可变样条,然后把所有样条分段结合成一个函数,就是最终的插值函数)
3.1 线性插值
两点确定一条直线,可以在两点间画一条直线,就可以把所有点连起来。【显然曲线不够光滑,原因:连接点处导数不相同】

3.2 二次样条
直线不行,用曲线代替,二次函数是最简单的曲线。
假设4个点,x0,x1,x2,x3,有3个区间,需要3个二次样条,每次二次样条为 ,故总计9个未知数。 ,故总计9个未知数。
1. x0,x3两个端点都有一个二次函数经过,可确定2个方程。
2. x1,x2两个中间点都有两个二次函数经过,可确定4个方程。
3. 中间点处必须连续,需要保证左右二次函数一阶导相等 [ 求导为 求导为  ] ]


可确定2个方程,此时有了8个方程
4. 假设第一方程的二阶导为0,即a1=0,又是一个方程,共计9个方程,联立即可求解。

# Python实现
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
"""
二次样条实现
"""
x = [3, 4.5, 7, 9]
y = [2.5, 1, 2.5, 0.5]
def calculateEquationParameters(x):
#parameter为二维数组,用来存放参数,sizeOfInterval是用来存放区间的个数
parameter = []
sizeOfInterval=len(x)-1
i = 1
#首先输入方程两边相邻节点处函数值相等的方程为2n-2个方程
while i < len(x)-1:
data = init(sizeOfInterval*3)
data[(i-1)*3]=x[i]*x[i]
data[(i-1)*3+1]=x[i]
data[(i-1)*3+2]=1
data1 =init(sizeOfInterval*3)
data1[i * 3] = x[i] * x[i]
data1[i * 3 + 1] = x[i]
data1[i * 3 + 2] = 1
temp=data[1:]
parameter.append(temp)
temp=data1[1:]
parameter.append(temp)
i += 1
#输入端点处的函数值。为两个方程,加上前面的2n-2个方程,一共2n个方程
data = init(sizeOfInterval*3-1)
data[0] = x[0]
data[1] = 1
parameter.append(data)
data = init(sizeOfInterval *3)
data[(sizeOfInterval-1)*3+0] = x[-1] * x[-1]
data[(sizeOfInterval-1)*3+1] = x[-1]
data[(sizeOfInterval-1)*3+2] = 1
temp=data[1:]
parameter.append(temp)
#端点函数值相等为n-1个方程。加上前面的方程为3n-1个方程,最后一个方程为a1=0总共为3n个方程
i=1
while i < len(x) - 1:
data = init(sizeOfInterval * 3)
data[(i - 1) * 3] =2*x[i]
data[(i - 1) * 3 + 1] =1
data[i*3]=-2*x[i]
data[i*3+1]=-1
temp=data[1:]
parameter.append(temp)
i += 1
return parameter
"""
对一个size大小的元组初始化为0
"""
def init(size):
j = 0
data = []
while j < size:
data.append(0)
j += 1
return data
"""
功能:计算样条函数的系数。
参数:parametes为方程的系数,y为要插值函数的因变量。
返回值:二次插值函数的系数。
"""
def solutionOfEquation(parametes,y):
sizeOfInterval = len(x) - 1
result = init(sizeOfInterval*3-1)
i=1
while i | 
