备注：知乎专栏更新了数理化生四科的基础讲义，更加完善的第二版已经更新，并且附上可以直接下载打印的PDF文档，里面可能还有一些小的笔误，订正后会再更新。

数学基础讲义大合集：数学基础讲义完整合集下载（含目录）

数学解题思路大合集：数学解题思路完整合集下载（含目录）

化学讲义合集：化学基础讲义合集

化学解题小合集：化学解题思路合集下载-2020年北京山东江苏浙江全国一二三

心得体会小合集：学习心得体会2021合集下载

物理和生物若急用可以先看知乎专栏里的，PDF文档待更新完善后再放出

下面是正文：

导数是函数中最后的重要部分，非常有用

1.1 什么是导数

导数是函数，完整地叫应该是“导函数”，通常习惯叫“导数”，它是依附于原函数存在的函数。

导数表示函数的变化趋势，既可以表示函数整体的变化趋势，也可以表示部分的变化趋势，还可以表示某个点的变化趋势。

导数也可以粗糙地理解为“函数在某处的切线的斜率”。

关于导数严谨的定义、是否存在的判别、计算和使用会在大学重头开始详细学习，高中只要简单地知道导数表示变化率、会求导数、会简单地用导数分析函数的性质即可。

函数f(x)的导数通常用f'(x)来表示，在f的右上角加上小撇。

当导数为正时，函数的变化率是正的，也就是递增的；

当导数为负时，函数的变化率是负的，也就是递减的；

当导数为0时，函数的变化率是0，也就是不增也不减，不变。

1.2 具体例子

举2个非常简单、非常形象、已经学过的例子

例1 速度

小学数学就学过速度，也叫速率，表示运动物体运动的距离随时间的变化率，s=vt的公式大家都会。

高中物理开始严谨一些，会更专业地区分“位移”“速度”（向量）和“距离”“速率”（无方向的标量），公式还是s=vt，但是表示的内容不同了。

这里我们就用简单的小学数学知识：

一辆小车在水平直线上匀速运动，它运动的速率v是不变的，因此运动的距离与时间成正比，也就是s=vt，这里，速率v就是距离s随t的变化率，距离s可以看作是时间t的函数。

为了方便起见，我们用x代表时间（代替t），f(x)代表距离，就是函数：f(x)=vx

这里v就是函数的变化率，该函数的导数就是：f'(x)=v（后面会学如何求导）

表示在任何时刻，小车距离变化的趋势都是v，时间每增加一个小小的x，距离就增加vx

例2 自由落体运动

初中物理开始学的难一些了，开始学速度随时间变化的运动了，比如自由落体运动，涉及到两个公式：

公式v=gt的含义大家应该都清楚，g是重力加速度，约为9.8 m/s^{2}，表示自由落体运动的物体的速度每秒会增加9.8m/s

还是为了方便起见，我们用x代表时间（代替t），g(x)代表速度，9.8代替g，上述公式就是函数： g(x)=9.8x

对该函数求导可得： g'(x)=9.8 ，这就是速度的变化趋势，任何时候速度都有随着时间增加9.8 m/s^{2}的趋势

另一个公式 s=gt^{2}/2 就要稍微麻烦点了，它表示物体从静止开始自由落体下落的距离和时间的关系

例1中我们用f(x)代替了距离s，这里也这么做；例1和上面都用x代替时间t，这里也这么做；也用具体数字9.8代替g，上述公式就变成了函数：

f(x)=9.8x^{2}/2 （这里的9.8和2不要约分，留着后面有用）

对这个函数求导可得： f'(x)=9.8x （具体如何求导后面会讲，这里先用结论），这就是下落距离随时间变化的关系，有没有觉得眼熟？

上面刚刚写了 g(x)=9.8x ，这里f'(x)也等于9.8x，因此f'(x)=g(x)

再回想例1中讲到的速度的定义：距离随时间的变化率，这里f'(x)就是距离随时间的变化率，也就是g(x)

自由落体运动的速度随时间改变，除了用加速度乘以时间外，直接对距离-时间的函数求导，得到的就是距离-时间的变化率，也就是速度。

以上两个例子应该比较形象地说明了什么是导数：就是变化率。

基本函数导数的推导超出了高中的要求，内容比较多，需要花相当时间和精力理解，对高考的帮助接近于零，因此不再给出，需要牢牢地记下来。

注意：

以下基本函数都是最最基本的函数，也就是说除了x和必须的部分外，不能有其他任何“杂质”。

比如单项式函数就是 x^{c} （c为常数且c≠0），不是 (x+2)^{c} 、 2x^{c}、 (2x)^{c} 等。

对数函数就是 lnx 、 log_{a}x ，不是 log_{a}(3x) 、 log_{a}(x+4) 等。

不能对x作出任何改变，

2.1 常数函数的导数

f(x)=c （c为常数）

f'(x)=0

任何常数函数的导数都为0

这很容易理解，常数函数的值是常数不发生变化，也不随着x变化而变化，变化率就是0。

对应到图像上，它的图像是一条水平的直线，任意位置的切线也是水平的。

举例如下图： f(x)=1 （左图，黑色）， f'(x)=0 （右图，红色）

2.2 单项式函数的导数

单项式函数：f(x)=x^{a} (a≠0)，它的导数为：f'(x)=ax^{a-1}

这里要特别注意的是a≠0，如果a=0就成了常数函数 f(x)=1

对任何非0的a，包括正数负数、整数分数、有理数无理数，上式都成立

这个公式可以理解为“降了一级”，就是任何单项式函数，取一次导数，就在它的前面乘以原次数，然后把次数减一。

比如次数是1： f(x)=x ，它的导数是 f'(x)=1*x^{1-1} ，也就是 f'(x)=1

比如次数是2： f(x)=x^{2} ，它的导数是 f'(x)=2*x^{2-1} ，也就是 f'(x)=2x

比如次数是1/2：f(x)=x^{1/2} ，（写作f(x)=\sqrt{x}更习惯），它的导数是 f'(x)=(1/2)*x^{1/2-1} ，也就是 f'(x)=x^{-1/2}/2，（写作f(x)=1/(2\sqrt{x})更习惯）

比如次数是3.5：f(x)=x^{3.5}，（也可以写作f(x)=x^{3}\sqrt{x}），它的导数是 f'(x)=3.5*x^{3.5-1} ，也就是 f'(x)=3.5x^{2.5}，（也可以写作f(x)=3.5x^{2}\sqrt{x}）

比如次数是-3：f(x)=x^{-3} ，（写作f(x)=1/x^{3}更习惯），它的导数是 f'(x)=(-3)*x^{-3-1} ，也就是 f'(x)=-3x^{-4}，（写作f(x)=-3/x^{4}更习惯）

比如次数是e：f(x)=x^{e} ，它的导数是 f'(x)=e*x^{e-1}

总之，只要次数不是0，只要直接在系数上乘以次数，再把次数减一就行了。

以下是上面几个例子像，要留意相同x值对应的原函数值和导数的值（e用2.71828近似）：

例1： f(x)=x （左图，黑色）， f'(x)=1 （右图，红色）

当x取任何值时，函数在该处的切线斜率不变，都为1

例2： f(x)=x^{2} （左图，黑色）， f'(x)=2x （右图，红色）

当x＜0时， f'(x)＜0 ，函数是递减的，且当x越大（负数绝对值越小）时，函数递减得越慢

当x＞0时， f'(x)＞0 ，函数是递增的，且当x越大时，函数递增得越快

当x=0时， f'(x)=0 ，函数在此处取最小值。

例3：f(x)=\sqrt{x} （左图，黑色）， f'(x)=1/(2\sqrt{x}) （右图，红色）

函数的定义域x∈[0，+∞)，导数在x=0处无意义

原函数是递增的，从图像上看增加得越来越慢

从导数上来看，导数始终是正的，印证了原函数是递增的，导数是递减的，从数学上印证了原函数增加得越来越慢

例4：f(x)=x^{3.5} （左图，黑色）， f'(x)=3.5x^{2.5} （右图，红色）

这个没太多好说的，导数＞0，原函数是递增的；并且导数是递增的，原函数越增越快

例5：f(x)=x^{-3} （左图，黑色）， f'(x)=-3x^{-4} （右图，红色）

原函数分为两段：

当x∈（-∞，0）时，函数值＜0，并且是单调递减的（负数绝对值越来越大）

当x∈（0，+∞）时，函数值＞0，并且也是单调递减的

导数也分为两段：

当x∈（-∞，0）时，导数值＜0，印证原函数递减，并且导数值递减，说明原函数越减越快（负数绝对值越增越快）

当x∈（0，+∞）时，导数值还是＜0，印证原函数还是递减，但此时导数值递增，说明原函数越减越慢

例6：f(x)=x^{e} （左图，黑色）， f'(x)=ex^{e-1} （右图，红色）

这个跟例4： f(x)=x^{3.5} 类似，主要是说明下指数是无理数的情况

2.3 指数函数的导数

指数函数 f(x)=a^{x} ，它的导数为： f'(x)=a^{x}lna

就是在原函数后面乘以lna就行，注意通常指数函数中底数a＞0且a≠1

特别的，当a=e（自然对数的底）时， f(x)=e^{x} 的导数为：f'(x)=e^{x}lne

由于lne=1，因此 f'(x)=e^{x}

下面举两个简单的例子：

例1：f(x)=2^{x} （黑色）， f'(x)=2^{x}ln2 （红色）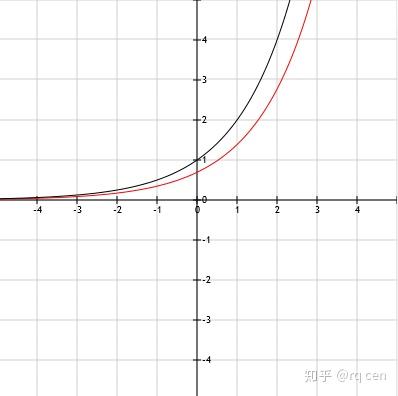

可以看出，导数的图像和原函数很像的，就是低了些，因为它多了系数ln2（约为0.693）

导数恒＞0，原函数是递增的

导数越来越大，原函数增加得越来越快

例2：f(x)=(1/2)^{x} （黑色）， f'(x)=(1/2)^{x}ln(1/2) （红色）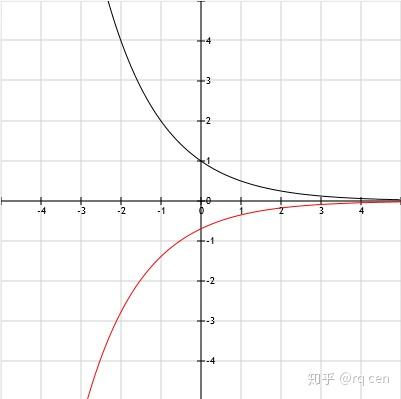

由于 ln(1/2)=ln2^{-1}=-ln2≈-0.693 ，导函数相当于原函数乘以了ln(1/2)，因此是＜0的，由此可知原函数是单调递减的

导函数随着x递增（负数绝对值减小），因此原函数递减得越来越慢

2.4 对数函数的导数

不知道有没有细心的同学注意到，在2.2 单项式函数的导数中，几乎全部的系数都被考虑到了，只有一个例外，就是当系数为0的情况，此时是常数函数。

但是对函数求导后，导数的次数也覆盖了几乎所有的次数，但是有个例外，就是次数为-1的情况，也就是对于任何基本的单项式函数求导，都得不到形如 x^{-1}的导数。

因为按照求导公式，当次数为0时，导数的次数是0-1=-1，但实际上当次数为0时，常数函数的导数恒为0。

对数函数弥补了这个“导数中x的次数为-1”的“空白”。

对数函数 f(x)=lnx ，它的导数为：f'(x)=1/x

对数函数 f(x)=log_{a}x ，它的导数为：f'(x)=1/(xlna)

这其实是一个公式

根据换底公式： log_{a}x=lnx/lna

由于a是常数，因此lna也是常数

因此f(x)=log_{a}x 也可以看做是 f(x)=lnx/lna

根据导数的性质（后面会讲），函数整体乘以一个常数，则它的导数就是原函数的导数乘以那个常数

因此 f(x)=lnx/lna的导数就是 f(x)=lnx 的导数再乘以 1/lna

具体例子：

左图中黑色曲线为 f(x)=lnx ，蓝色曲线为 g(x)=log_{2}x （或 g(x)=(1/ln2)*lnx ）

右图中红色曲线为 f'(x)=1/x ，粉色曲线为 g'(x)=1/(x*ln2)

可以看出，两个函数都是递增的，它们的导数也都是正的

两个函数递增得越来越慢（图像越来越“趴下”），导数也都是逐渐减小的

当x＞1时，0＜f(x)＜g(x)，因为g(x)=f(x)/ln2，而ln2＜1

当x＜1时，g(x)＜f(x)＜0，因为|g(x)=f(x)/ln2|，负数的绝对值越大，负数越小

二者的导数都是＞0的，因此g'(x)＞f'(x)

2.5 三角函数的导数

对三角函数 f(x)=sinx ，它的导数为： f'(x)=cosx

对三角函数 f(x)=cosx ，它的导数为： f'(x)=-sinx

对三角函数 f(x)=tanx ，它的导数为： f'(x)=1/cos^{2}x=sec^{2}x

对三角函数 f(x)=cotx ，它的导数为： f'(x)=-1/sin^{2}x=-csc^{2}x

对三角函数 f(x)=secx ，它的导数为： f'(x)=sinx/cos^{2}x=secx*tanx

对三角函数 f(x)=cscx ，它的导数为： f'(x)=-cos^{2}x/sinx=-secx*cotx

这里面前2个最重要，需要牢记，也最容易记。

后面4个可以通过很重要同时也很基本的运算推导出来，后面会讲

这个的图像没什么意思，就不画了

有个有趣的周期性质可以了解下：

f(x)=sinx

f'(x)=cosx

f''(x)=-sinx

f'''(x)=-cosx

f''''(x)=sinx

每求4次导数就构成一个循环。

2.6 反三角函数的导数

对反三角函数 f(x)=arcsinx ，它的导数为： f'(x)=1/\sqrt{1-x^{2}}

对反三角函数 f(x)=arccosx ，它的导数为：f'(x)=-1/\sqrt{1-x^{2}}

对反三角函数 f(x)=arctanx ，它的导数为： f'(x)=1/(1+x^{2})

对反三角函数 f(x)=arccotx ，它的导数为：f'(x)=-1/(1+x^{2})

对反三角函数，要特别留意他们的定义域和值域，对他们的导数也是如此

由于反三角函数的导数的题目并不多，训练的机会有限，因此更要牢记！

小结

以上是基本函数的导数，注意，是基本函数，没有夹带任何其他东西。

比如单项式就是 x^{2} 、 1/x 、 \sqrt[5]{x}这种，不是 2x^{2} 、 -7/x 、 \sqrt[5]{4x}

比如对数就是 lnx 、 log_{8}x 这种，不是 ln(x/4) 、 log_{8}(5x^{2})

稍微复杂点的情况接下来马上就讲

最后，也是最重要的，由于导数是新接触的运算，没有学习运算的本质推导，因此一定要多做题，增加熟练度，至少要达到与指数对数运算相当的熟练程度。

此外，就算学会了基本函数的导数的推导，对记忆公式的帮助也不大。

下面是导数的运算，建立在上面的基本函数的导数的基础上

有些可以很直观的理解，有些不可以

3.1 函数乘以（除以）常数的导数

只讨论乘以常数，除以看作乘以该常数的倒数即可。

若函数f(x)的导数为f'(x)，则函数g(x)=a*f(x)的导数为：g'(x)=a*f'(x)

直观理解很简单，就是在原函数的导数前乘以该常数即可。

比如函数f(x)=x^{10} 的导数为 f'(x)=10x^{9}

那么函数 g(x)=2f(x)=2x^{10} 的导数为： g'(x)=2*f'(x)=2*10x^{9}=20x^{9}

再比如函数 f(x)=lnx 的导数为 f'(x)=1/x，

那么函数 g(x)=(-1/2)lnx 的导数为 g'(x)=(-1/2)*(1/x)=-1/(2x)

特别注意

常数a是与函数整体相乘，而不是直接与x相乘。

沿用上面的例子：

比如函数f(x)=x^{10} 的导数为 f'(x)=10x^{9}

那么函数 g(x)=(2x)^{10} 的导数就不能用这个方法来求

而是要先化成常数*原函数的形式： g(x)=2^{10}*x^{10}

因此 g'(x)=2^{10}*f'(x)=2^{10}*10x^{9}

还有其他更通用的求法，本节后面会讲到

再比如函数 f(x)=lnx 的导数为 f'(x)=1/x，

那么函数 g(x)=ln(2x) 的导数就不能用这个方法来求，

可以把它化为： g(x)=ln2+lnx ，分别求导后相加（3.2中马上会讲）

得到 g'(x)=0+1/x=1/x ，竟然和f(x)的导数相同！（没错，就是相同）

3.2函数相加（减）的导数

若函数f(x)、g(x)的导数分别为f'(x)、g'(x)，则函数f(x)+g(x)的导数为f'(x)+g'(x)

f(x)-g(x)的导数就是f'(x)-g'(x)，减法看作加上-1*函数即可

这个很容易理解，两个函数相加减，他们变化的趋势也是直接相加减，就是很直接的线性关系

比如两个一次函数：

f(x)=4x，它的导数为f'(x)=4

g(x)=6x，它的导数为g'(x)=6

那么h(x)=f(x)+g(x)=4x+6x=10x，直接对它求导，得到的导数就是h'(x)=10

这和直接4+6=10的结果是相同的

这样一来，对于多项式函数，就可以逐项求导，然后相加即可。

比如 f(x)=4x^{4}+2x^{2}+x-1/x^{2}-\sqrt[4]{x}+8

则 f'(x)=16x^{3}+4x+1-(-2)x^{-3}-(1/4)x^{-3/4}+0

再比如其他一些混合相加的函数

f(x)=2x^{3}+log_{4}x+5^{x}+cosx

则 f'(x)=6x^{2}+1/(xln4)+5^{x}ln5-sinx

特别注意

多个函数相加的求导也是一样的，分别求导，再加起来即可

这里的函数之间只能是简单的相加（减）关系，不能是相乘、复合的关系

比如 f(x)=ln(2x^{3}+4) 、f(x) f(x)=sinx*cosx 、 f(x)=tan(x^{2}) 就不符合此情况

后面会讲

3.3 函数相乘的导数

若函数f(x)、g(x)的导数分别为f'(x)、g'(x)，那么函数h(x)=f(x)*g(x)的导数为：

h'(x)=f'(x)*g(x)+g'(x)*f(x)

就是说如果两个函数相乘，所得函数的导数就是一个的导数乘以另一个的原函数，加上另一个的导数乘以这个的原函数

相乘的两个函数分别作为原函数出现一次、作为导数出现一次，二者的地位是等同的

举两个具体的例子：

函数 f(x)=3x^{3} ， g(x)=2sinx，

根据前面的内容可以知道 f'(x)=9x^{2} ， g'(x)=2cosx

则函 h(x)=6x^{3}*sinx 的导数为：

h'(x)=f'(x)*g(x)+g'(x)*f(x)

=9x^{2}*2sinx+2cosx*3x^{3}

=18x^{2}sinx+6x^{3}cosx

举个有趣的例子验证下：

函数 f(x)=2x^{2} , g(x)=3x^{3} ， h(x)=f(x)*g(x)=6x^{5}

直接用前面的方法可以直接求得： f'(x)=4x ， g'(x)=9x^{2} ， h'(x)=30x^{4}

现在再用本小节的方法“麻烦”地求一遍：

h'(x)=f'(x)g(x)+g'(x)f(x)

=4x*3x^{3}+9x^{2}*2x^{2}

=12x^{4}+18x^{4}

=30x^{4}

结果是相同的

多个函数相乘的求导，就需要一步一步算了，先把一个剥离出来，其余的看做整体；然后把其余的剥离出来一个，其余的其余看做一个整体......直到最后只剩两个，然后依次计算

比如四个：

[f(x)g(x)h(x)k(x)]'=f'(x)[g(x)h(x)k(x)]+[g(x)h(x)k(x)]'f(x)

=f'(x)[g(x)h(x)k(x)]+[g'(x)h(x)k(x)+(h(x)k(x))'g(x)]f(x)

=f'(x)[g(x)h(x)k(x)]+g'(x)h(x)k(x)f(x)+[h'(x)k(x)+k'(x)h(x)]g(x)f(x)

=f'(x)[g(x)h(x)k(x)]+g'(x)h(x)k(x)f(x)+h'(x)k(x)g(x)f(x)+k'(x)h(x)g(x)f(x)

（这里中括号小括号比较多，一层套一层，又是f(x)g(x)h(x)k(x)的，容易搞混和看晕，建议亲自手写分解下）

很容易用数学归纳法证明，多个函数相乘的求导，就是对其中的每个函数求导，与其他的原函数相乘，然后加起来

特别注意

只能是两个函数相乘，不能涉及到复合，复合后面会讲

相除并不是简单的乘以相反数，虽然事实上可以这么做，可是很多复杂函数的相反数就更复杂了，相除的下小节就讲

3.4 函数相除的导数

若函数f(x)、g(x)的导数分别为f'(x)、g'(x)，则函数h(x)=f(x)/g(x)的导数为：

h'(x)=[f'(x)*g(x)-g'(x)*f(x)]/g^{2}(x)

就是说如果一个函数除以另一个函数，那么这个除式的导数就是：分子的导数乘以分母，减去分母的导数乘以分子，总的再除以分母的平方。

这个记起来要麻烦些，仍然是一个求导乘以另一个不求导，区别在于是相减，并且分母还要平方。

举两个具体的例子：

f(x)=lnx ， g(x)=x^{2}/2 ， h(x)=2lnx/x^{2}

根据前面的内容很容易求得： f'(x)=1/x ， g'(x)=x ，根据本小结内容：

h'(x)=[f'(x)*g(x)-g'(x)*f(x)]/g^{2}(x)

=[(1/x)*(x^{2}/2)-x*lnx]/(x^{4}/4)

=(2-4lnx)/x^{3}

再举个有趣的例子验证下：

f(x)=x^{4}+2x^{2}-x ， g(x)=x^{2} ， h(x)=f(x)/g(x)=(x^{4}+2x^{2}-x)/x^{2}

很容易求出： f'(x)=4x^{3}+4x-1 ， g'(x)=2x

方法一：用本小结的方法

h'(x)=[(4x^{3}+4x-1)*x^{2}-2x*(x^{4}+2x^{2}-x)]/(x^{2})^{2}

=(4x^{5}+4x^{3}-x^{2}-2x^{5}-4x^{3}+2x^{2})/x^{4}

=(2x^{5}+x^{2})/x^{4}

=2x+1/x^{2}

方法二：先把h(x)化为普通的多项式函数再求导

h(x)=x^{2}+2-1/x

h'(x)=2x+0-(-1/x^{2})=2x+1/x^{2}

两种解法的结果是一样的

3.5 复合函数的导数

若函数f(x)、g(x)的导数分别为f'(x)、g'(x)，则复合函数h(x)=f(g(x))的导数为：

h'(x)=f'(g(x))*g'(x)

对复合函数的求导，先把里面的函数看做一个整体，对外面的函数进行求导，然后再只对里面的函数求导，然后乘起来

下面举2个例子：

例1： f(x)=(x^{2}+1)^{2}

先用复合函数的求导法则，令 g(x)=x^{2}， h(x)=x^{2}+1 ，则 f(x)=g(h(x))

f'(x)=g'(h(x))*h'(x)

=[2*(x^{2}+1)]*(2x+0)

=4x^{3}+4x

换个方法先把原函数展开：

f(x)=x^{4}+2x^{2}+1 ，

再求导得： f'(x)=4*x^{3}+2*(2x)+0=4x^{3}+4x

结果是一样的

例二： f(x)=ln(x^{3}+cosx) （x＞1）

令 g(x)=lnx ， h(x)=x^{3}+cosx ，则 f(x)=g(h(x))

因此 f'(x)=g'(h(x))*h'(x)=[1/(x^{3}+cosx)]*(3x^{2}-sinx)

如果遇到多重复合函数的话，只要一层一层套下去就可以了，比如

f(x)=[ln(sin(x^{2}))]^{3}

先对最外的三次方求导，再对下一层的ln求导，再对下一层的sin求导，再对最后的二次方求导

f'(x)=3[ln(sin(x^{2}))]^{2}*(1/sin(x^{2}))*cos(x^{2})*(2x)

特别注意

复合函数对外层求导，一定是要把里面的函数看作一个整体进行运算，不要做任何变化

小结

由于是新学的内容，导数运算法则也同样需要大量的练习来掌握和熟练，等到熟练后可以不必再化成f(x)*g(x)、f(g(x))的形式，直接解决

的推导高中也不需要掌握，况且掌握后对熟悉以上运算也毫无帮助。

导数的应用主要有两个：判断单调性和求极值点。

4.1 判断单调性

导数反应的是函数的变化率，既可以反应某个点上函数的变化趋势，也可以反应某个区间内函数的变化趋势。

首先要判断函数在该区间内是否都存在导数，比如分母不能为0，对数的真数必须为正，等等1

如果函数在某个区间内导数恒＞0，则函数在这个区间内是单调递增的；

如果函数在某个区间内导数恒＜0，则函数在这个区间内是单调递减的；

如果函数在某个区间内导数恒=0，则函数在这个区间内是不增不减的。

用最简单最熟悉的二次函数为例：

例1

f(x)=x^{2}-2x-3

先用传统的凑平方法来判断它的单调性：

f(x)=(x-1)^{2}-4

不用多说，当x＞1时，函数单调递增，当x＜1时，函数单调递减

再用导数的方法，对函数求导得：

f'(x)=2x-2

当x＞1时，f'(x)＞0，函数单调递增；当x＜1时，f'(x)＜0，函数单调递减

两者的结论是相同的

对于二次函数这种简单又熟悉的函数来说，导数并没有显得很好用，下面来看个稍微复杂些的

例2

f(x)=x^{2}-lnx （x＞0）

这个看起来稍微复杂些了

对它求导即可：

f'(x)=2x-1/x

现在来不等式： 2x-1/x＞0

由于x＞0，等式两边都乘以x得： 2x^{2}-1＞0

解得： x＞1/\sqrt{2} 或 x＜-1/\sqrt{2}

根据函数的定义域去掉负的可得： x＞1/\sqrt{2}

因此当x＞1/\sqrt{2}时，函数单调递增；

同样的解不等式2x-1/x＜0 可得 x＜1/\sqrt{2}

因此当 0＜x＜1/\sqrt{2} 时，函数单调递减。

不解不等式解方程

如果解不等式有些困难的话，直接解方程也可以：

2x-1/x=0

得到唯一的正根 x=1/\sqrt{2}

可以据此判断，函数在定义域内只有这一个导数为0的点。

并且由于函数在定义域内处处导数都有意义，因此x=1/\sqrt{2}就是函数单调性的分界点

只需要随便取几个值代入导数计算即可

这里的取值有个小技巧：要么尽量取极端的数字，比如很大或很小的数字；要么取很好算的数字，比如0、1之类的

这个例子里由于定义域的关系不能取0

就分别取1/e (＜1/\sqrt{2} ) 和1(＞1/\sqrt{2} )吧

f'(1/e)=2/e-e，代入e≈2.71828,得：2/e＜1，e＞2，因此f'(1/e)＜0，当 0＜x＜1/\sqrt{2} 时，函数单调递减

f'(1)=2-1=1＞0（是不是很好算），因此当 x＞1/\sqrt{2} 时，函数单调递增

上面的例子中由于出现了对数，因此判断上较为麻烦，大多数例子中往往可以用简单的或特殊的数字很容易进行判断，比如下面这个例子：

例3

求函数 f(x)=x^{3}+2x^{2}-4x 的单调区间

f'(x)=3x^{2}+4x-4

解方程 3x^{2}+4x-4=0 得：

x_{1}=2/3 ， x_{2}=-2

也就是说函数的单调区间分别为(-∞，-2)（-2，2/3）（2/3，﹢∞）三个

分别代入-100（两头的数字越极端越好）、0（0是个很好算的数字）、1（1也是个很好算的数字，也可以取极端的100）得：

f'(-100)=3000000-400-4＞0

f'(0)=-4＜0

f'(1)=3+4-4=3＞0

因此函数在(-∞，-2)递增，在（-2，2/3）递减，在（2/3，﹢∞）递增

4.2 判断函数的极值和最值

首先要明晰两个概念：函数的极值和最值

函数的最值就是我们通常认为的函数的最大值、最小值，也就是整个函数上面函数值最大或最小的点，有的函数有，有的没有

比如二次函数如果二次项系数为正，就有最小值没有最大值；如果二次项系数为负，就有最大值没有最小值

一次函数既没有最大值也没有最小值

标准正弦函数既有最大值（+1）又有最小值（-1）

函数的极值：极大值或极小值，是指在函数的这个点附近，没有比它更大或更小的值了

什么叫附近呢？这个说法很不规范

可以这么理解，在高中遇到的函数中，

在导数的不分段的定义域内，如果某个点处导数为0，那么它就是一个极值；

如果函数在某处有定义，但是导数在该处不存在，那么它有可能也是一个极值

如果这个点比它两侧的点都大，也就是左边递增右边递减，它就是极大值

如果这个点比它两侧的点都笑，也就是左边递减右边递增，它就是极小值

要注意的是，极大值极小值只是某个点的特殊性质，不意味着它就是函数的最大值或最小值，有时候是，有时候不是

并且，同一个函数的极大值不一定就比极小值小，因为极大值极小值只反应这个点本身和它附近的情况

如何具体判断是极大值还是极小值呢，除了上述根据两边的单调性判断外，还有个办法：

求二阶导数，也就是对导数再求导数，记作f''(x)（右上角有两撇）

在某处f'(x)=0，且f''(x)＜0，那么该处就是函数的极大值；

在某处f'(x)=0，且f''(x)＞0，那么该处就是函数的极小值；

对于该处导数不存在，那就不能用这个方法，只能试了。

就以前面的3个例子为例：

例1

f(x)=x^{2}-2x-3

f'(x)=2x-2

x=1（点（1，-4））是函数的一个极值点

f''(x)=2

f''(1)＞0 （实际上f''(x)恒＞0）

因此点（1，-4）是函数的一个极小值点

又因为该函数在该点左侧递减，在右侧递增，因此该点也是该函数的最小值点

例2

f(x)=x^{2}-lnx （x＞0）

f'(x)=2x-1/x

x=1/\sqrt{2}是该函数的一个极值点

f''(x)=2+1/x^{2}

f''(\sqrt{2})＞0 （实际上f''(x)恒＞0）

因此 x=1/\sqrt{2} 时是该函数的一个极小值点

和例一相同的原因，此处也是该函数的最小值点

下面画出它的图像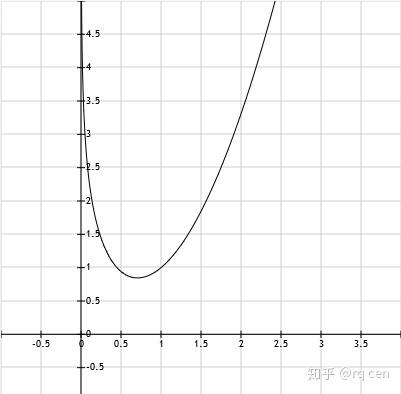

例3

f(x)=x^{3}+2x^{2}-4x

f'(x)=3x^{2}+4x-4

求得两个极值点：x_{1}=2/3 ， x_{2}=-2

f''(x)=6x+4

f''(2/3)=8 ＞0，是极小值

f''(-2)=-8 ＜0，是极大值

由于函数在(-∞，-2)递增，在（-2，2/3）递减，在（2/3，﹢∞）递增

当x非常非常负，比如-1000000000000时，函数值是非常非常小，肯定比f(2/3)要小，因此f(2/3)不是函数的最小值

同理，当x非常非常大，比如10000000000时，函数值非常非常大，肯定比f(-2)大，因此f(-2)不是函数的最大值

该函数的最大最小值不存在

它的图像为：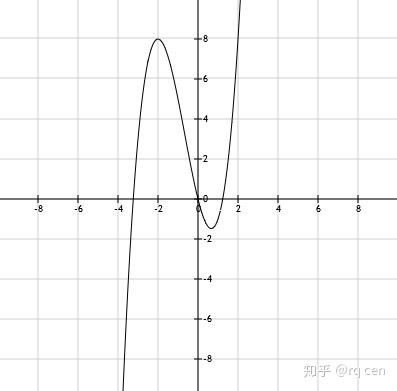

4.3 绘制函数的图像

绘制函数图像对判断和解决一些问题有比较直观的帮助，尽管具体的数值和判断需要通过严谨的数学推导来完成，但是通过图像得到的直观了解对构建思路和猜测答案很有帮助。

在最开始的几章里，已经讲了一些基本函数的图像，如果遇到相对复杂一些的函数，该怎么画出它们的图像呢？这里简单讲下几个实用的步骤：

第一步：确定关键点

主要有以下几个点：与x轴的交点、与y轴的交点、导数为0的点、函数无定义的点（比如分母为0）

第二步：确定单调性

根据导数为0的点和无定义的点，把函数分段，然后分别求这几段区间内导数的正负，从而确定函数的单调性

求函数的二阶导数（导数的导数），验证导数为0的点是极大值还是极小值

第三步：用平滑的曲线连接各特殊点

如果想更加精确的话，再求出二阶导数为0的点

二阶导数为正的区间，函数的曲线是开口向上的（类似于指数函数的图像，越增越快或越减越慢）

二阶导数为负的区间，函数的曲线是开口向下的（类似于对数函数的图像，越增越慢或越减越快）

导数是高中数学里最后最难的部分。

由于是全新的内容，全新的公式，全新的运算规律，因此需要大量的运算来熟悉，就像当初刚学指数和对数那样。

然而指数和对数是基于乘法和幂运算的，有基础可循。导数在高中数学中不讲推导，只是生硬简单粗浅地介绍概念，直接讲公式和运算规律，因此掌握起来更难。不过即便学会推导过程，对记忆公式也没有很大帮助，还是得靠多练。

导数虽然很新，感觉上很难，但其实具体题目的难点并不在导数的运算上，而是主要在于知道怎么运用导数来判断单调性和大小等函数的性质。

有兴趣和空闲详细学习了解推导过程的同学，推荐《普林斯顿微积分读本》（美国人Adrian Banner著），这本书是教材中比较容易理解的。